Disentangling Interpretable Factors with Supervised Independent Subspace Principal Component Analysis

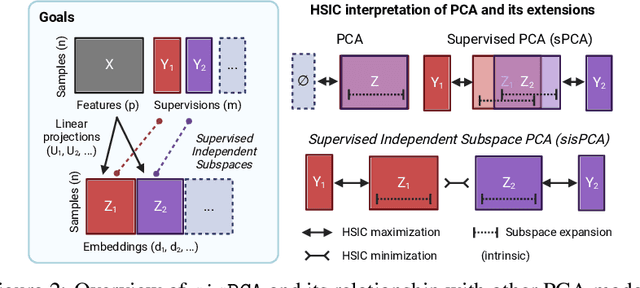
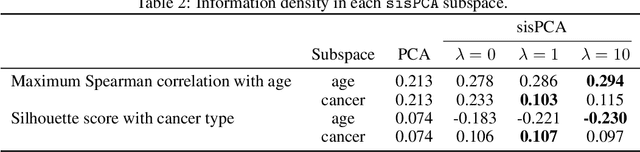
The success of machine learning models relies heavily on effectively representing high-dimensional data. However, ensuring data representations capture human-understandable concepts remains difficult, often requiring the incorporation of prior knowledge and decomposition of data into multiple subspaces. Traditional linear methods fall short in modeling more than one space, while more expressive deep learning approaches lack interpretability. Here, we introduce Supervised Independent Subspace Principal Component Analysis ($\texttt{sisPCA}$), a PCA extension designed for multi-subspace learning. Leveraging the Hilbert-Schmidt Independence Criterion (HSIC), $\texttt{sisPCA}$ incorporates supervision and simultaneously ensures subspace disentanglement. We demonstrate $\texttt{sisPCA}$'s connections with autoencoders and regularized linear regression and showcase its ability to identify and separate hidden data structures through extensive applications, including breast cancer diagnosis from image features, learning aging-associated DNA methylation changes, and single-cell analysis of malaria infection. Our results reveal distinct functional pathways associated with malaria colonization, underscoring the essentiality of explainable representation in high-dimensional data analysis.

MREC: a fast and versatile framework for aligning and matching point clouds with applications to single cell molecular data

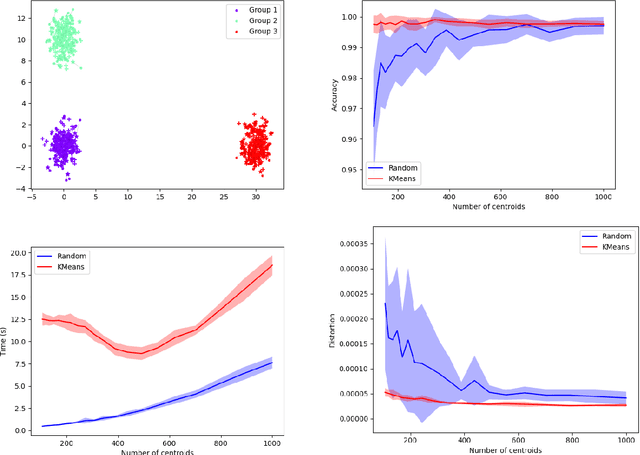
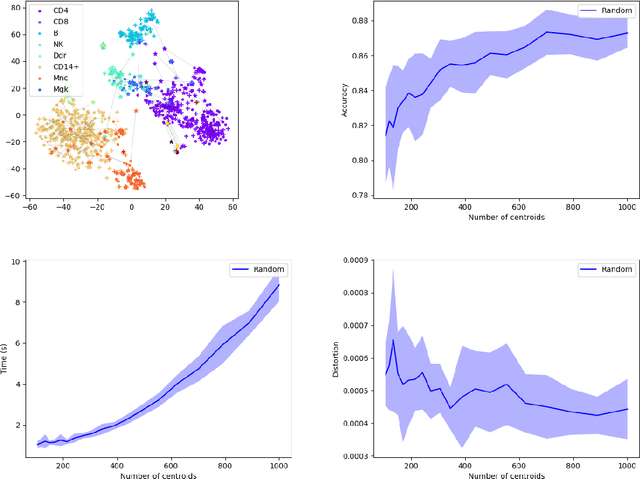
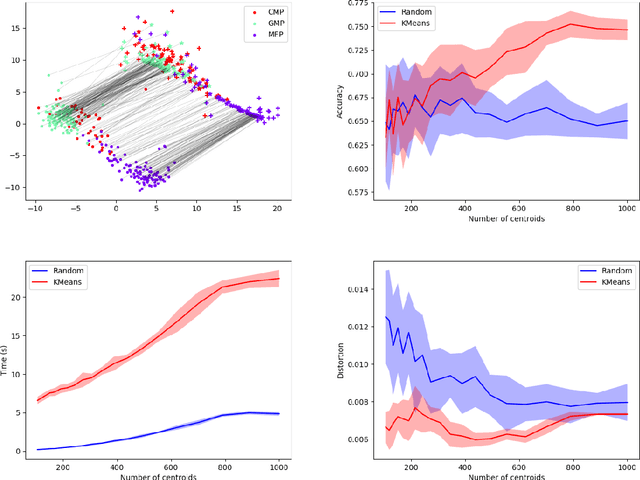
Comparing and aligning large datasets is a pervasive problem occurring across many different knowledge domains. We introduce and study MREC, a recursive decomposition algorithm for computing matchings between data sets. The basic idea is to partition the data, match the partitions, and then recursively match the points within each pair of identified partitions. The matching itself is done using black box matching procedures that are too expensive to run on the entire data set. Using an absolute measure of the quality of a matching, the framework supports optimization over parameters including partitioning procedures and matching algorithms. By design, MREC can be applied to extremely large data sets. We analyze the procedure to describe when we can expect it to work well and demonstrate its flexibility and power by applying it to a number of alignment problems arising in the analysis of single cell molecular data.

Black Box FDR

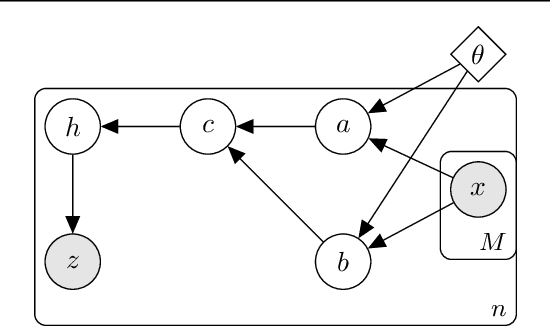
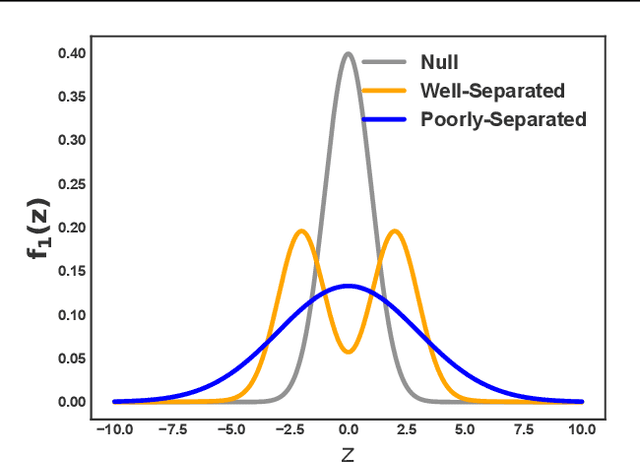
Analyzing large-scale, multi-experiment studies requires scientists to test each experimental outcome for statistical significance and then assess the results as a whole. We present Black Box FDR (BB-FDR), an empirical-Bayes method for analyzing multi-experiment studies when many covariates are gathered per experiment. BB-FDR learns a series of black box predictive models to boost power and control the false discovery rate (FDR) at two stages of study analysis. In Stage 1, it uses a deep neural network prior to report which experiments yielded significant outcomes. In Stage 2, a separate black box model of each covariate is used to select features that have significant predictive power across all experiments. In benchmarks, BB-FDR outperforms competing state-of-the-art methods in both stages of analysis. We apply BB-FDR to two real studies on cancer drug efficacy. For both studies, BB-FDR increases the proportion of significant outcomes discovered and selects variables that reveal key genomic drivers of drug sensitivity and resistance in cancer.