Wesley Tansey
Addressing the Cold-Start Problem for Personalized Combination Drug Screening
Sep 09, 2025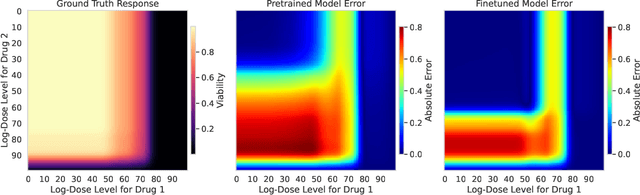
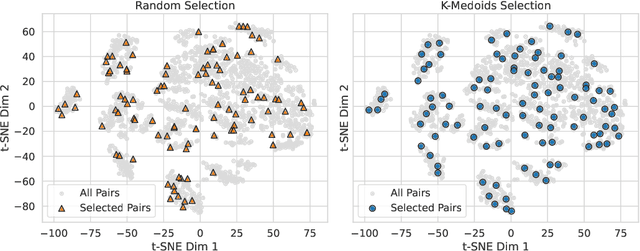
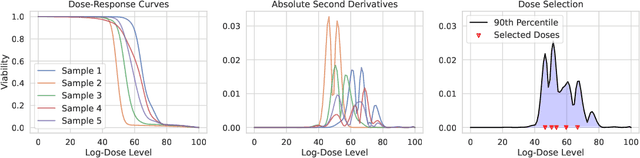
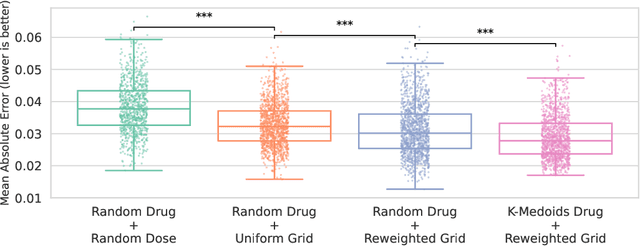
Abstract:Personalizing combination therapies in oncology requires navigating an immense space of possible drug and dose combinations, a task that remains largely infeasible through exhaustive experimentation. Recent developments in patient-derived models have enabled high-throughput ex vivo screening, but the number of feasible experiments is limited. Further, a tight therapeutic window makes gathering molecular profiling information (e.g. RNA-seq) impractical as a means of guiding drug response prediction. This leads to a challenging cold-start problem: how do we select the most informative combinations to test early, when no prior information about the patient is available? We propose a strategy that leverages a pretrained deep learning model built on historical drug response data. The model provides both embeddings for drug combinations and dose-level importance scores, enabling a principled selection of initial experiments. We combine clustering of drug embeddings to ensure functional diversity with a dose-weighting mechanism that prioritizes doses based on their historical informativeness. Retrospective simulations on large-scale drug combination datasets show that our method substantially improves initial screening efficiency compared to baselines, offering a viable path for more effective early-phase decision-making in personalized combination drug screens.
Treatment response as a latent variable
Feb 12, 2025Abstract:Scientists often need to analyze the samples in a study that responded to treatment in order to refine their hypotheses and find potential causal drivers of response. Natural variation in outcomes makes teasing apart responders from non-responders a statistical inference problem. To handle latent responses, we introduce the causal two-groups (C2G) model, a causal extension of the classical two-groups model. The C2G model posits that treated samples may or may not experience an effect, according to some prior probability. We propose two empirical Bayes procedures for the causal two-groups model, one under semi-parametric conditions and another under fully nonparametric conditions. The semi-parametric model assumes additive treatment effects and is identifiable from observed data. The nonparametric model is unidentifiable, but we show it can still be used to test for response in each treated sample. We show empirically and theoretically that both methods for selecting responders control the false discovery rate at the target level with near-optimal power. We also propose two novel estimands of interest and provide a strategy for deriving estimand intervals in the unidentifiable nonparametric model. On a cancer immunotherapy dataset, the nonparametric C2G model recovers clinically-validated predictive biomarkers of both positive and negative outcomes. Code is available at https://github.com/tansey-lab/causal2groups.
DIET: Conditional independence testing with marginal dependence measures of residual information
Aug 18, 2022



Abstract:Conditional randomization tests (CRTs) assess whether a variable $x$ is predictive of another variable $y$, having observed covariates $z$. CRTs require fitting a large number of predictive models, which is often computationally intractable. Existing solutions to reduce the cost of CRTs typically split the dataset into a train and test portion, or rely on heuristics for interactions, both of which lead to a loss in power. We propose the decoupled independence test (DIET), an algorithm that avoids both of these issues by leveraging marginal independence statistics to test conditional independence relationships. DIET tests the marginal independence of two random variables: $F(x \mid z)$ and $F(y \mid z)$ where $F(\cdot \mid z)$ is a conditional cumulative distribution function (CDF). These variables are termed "information residuals." We give sufficient conditions for DIET to achieve finite sample type-1 error control and power greater than the type-1 error rate. We then prove that when using the mutual information between the information residuals as a test statistic, DIET yields the most powerful conditionally valid test. Finally, we show DIET achieves higher power than other tractable CRTs on several synthetic and real benchmarks.
Quantile regression with ReLU Networks: Estimators and minimax rates
Oct 27, 2020
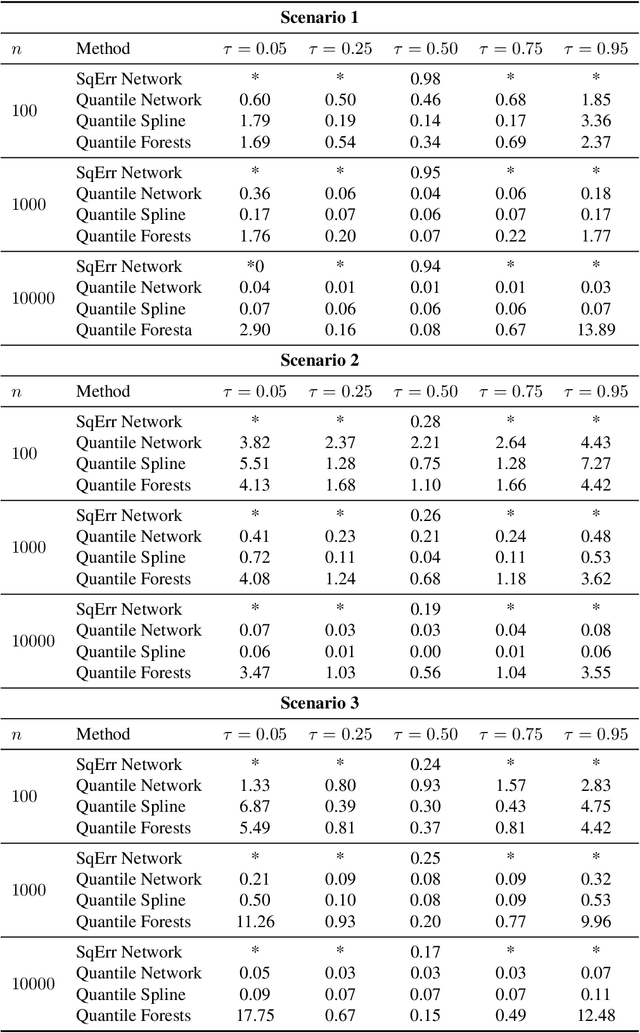
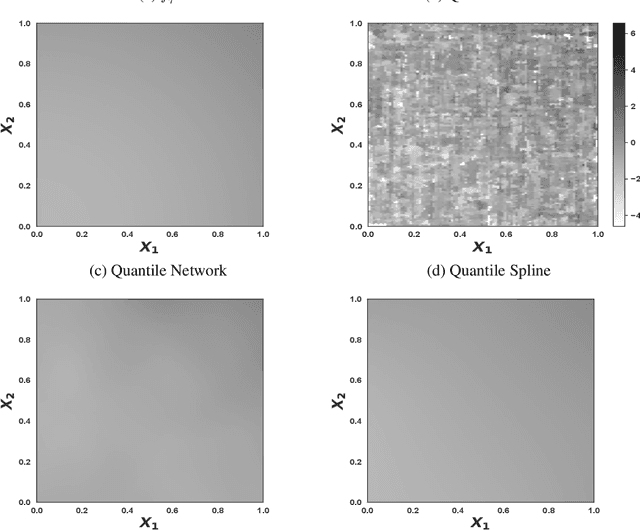

Abstract:Quantile regression is the task of estimating a specified percentile response, such as the median, from a collection of known covariates. We study quantile regression with rectified linear unit (ReLU) neural networks as the chosen model class. We derive an upper bound on the expected mean squared error of a ReLU network used to estimate any quantile conditional on a set of covariates. This upper bound only depends on the best possible approximation error, the number of layers in the network, and the number of nodes per layer. We further show upper bounds that are tight for two large classes of functions: compositions of H\"older functions and members of a Besov space. These tight bounds imply ReLU networks with quantile regression achieve minimax rates for broad collections of function types. Unlike existing work, the theoretical results hold under minimal assumptions and apply to general error distributions, including heavy-tailed distributions. Empirical simulations on a suite of synthetic response functions demonstrate the theoretical results translate to practical implementations of ReLU networks. Overall, the theoretical and empirical results provide insight into the strong performance of ReLU neural networks for quantile regression across a broad range of function classes and error distributions. All code for this paper is publicly available at https://github.com/tansey/quantile-regression.
Deep Direct Likelihood Knockoffs
Jul 31, 2020



Abstract:Predictive modeling often uses black box machine learning methods, such as deep neural networks, to achieve state-of-the-art performance. In scientific domains, the scientist often wishes to discover which features are actually important for making the predictions. These discoveries may lead to costly follow-up experiments and as such it is important that the error rate on discoveries is not too high. Model-X knockoffs enable important features to be discovered with control of the FDR. However, knockoffs require rich generative models capable of accurately modeling the knockoff features while ensuring they obey the so-called "swap" property. We develop Deep Direct Likelihood Knockoffs (DDLK), which directly minimizes the KL divergence implied by the knockoff swap property. DDLK consists of two stages: it first maximizes the explicit likelihood of the features, then minimizes the KL divergence between the joint distribution of features and knockoffs and any swap between them. To ensure that the generated knockoffs are valid under any possible swap, DDLK uses the Gumbel-Softmax trick to optimize the knockoff generator under the worst-case swap. We find DDLK has higher power than baselines while controlling the false discovery rate on a variety of synthetic and real benchmarks including a task involving a large dataset from one of the epicenters of COVID-19.
Bayesian Tensor Filtering: Smooth, Locally-Adaptive Factorization of Functional Matrices
Jun 10, 2019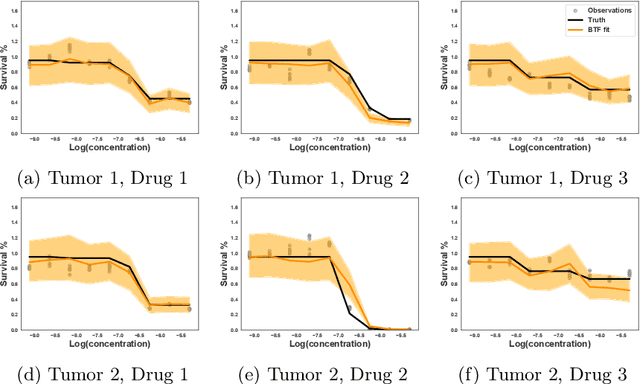

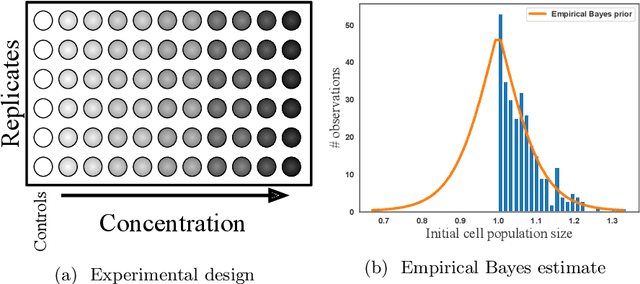
Abstract:We consider the problem of functional matrix factorization, finding low-dimensional structure in a matrix where every entry is a noisy function evaluated at a set of discrete points. Such problems arise frequently in drug discovery, where biological samples form the rows, candidate drugs form the columns, and entries contain the dose-response curve of a sample treated at different concentrations of a drug. We propose Bayesian Tensor Filtering (BTF), a hierarchical Bayesian model of matrices of functions. BTF captures the smoothness in each individual function while also being locally adaptive to sharp discontinuities. The BTF model is agnostic to the likelihood of the underlying observations, making it flexible enough to handle many different kinds of data. We derive efficient Gibbs samplers for three classes of likelihoods: (i) Gaussian, for which updates are fully conjugate; (ii) Binomial and related likelihoods, for which updates are conditionally conjugate through P{\'o}lya--Gamma augmentation; and (iii) Black-box likelihoods, for which updates are non-conjugate but admit an analytic truncated elliptical slice sampling routine. We compare BTF against a state-of-the-art method for dynamic Poisson matrix factorization, showing BTF better reconstructs held out data in synthetic experiments. Finally, we build a dose-response model around BTF and show on real data from a multi-sample, multi-drug cancer study that BTF outperforms the current standard approach in biology. Code for BTF is available at https://github.com/tansey/functionalmf.
Interpreting Black Box Models with Statistical Guarantees
Mar 29, 2019
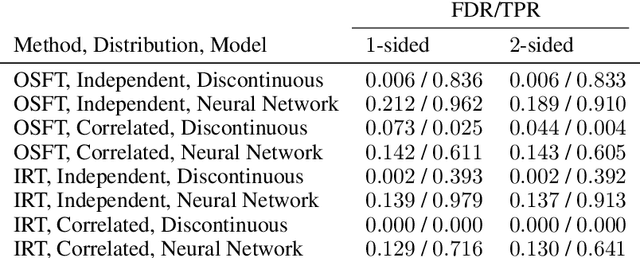
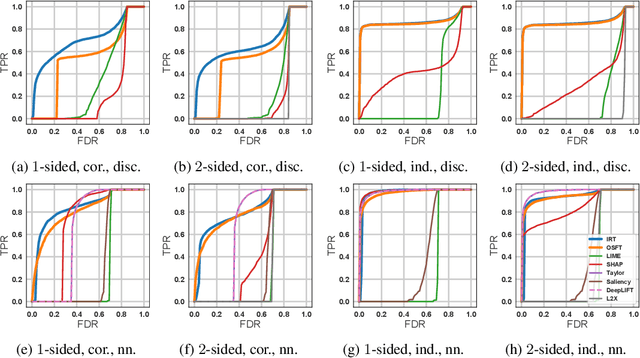

Abstract:While many methods for interpreting machine learning models have been proposed, they are frequently ad hoc, difficult to evaluate, and come with no statistical guarantees on the error rate. This is especially problematic in scientific domains, where interpretations must be accurate and reliable. In this paper, we cast black box model interpretation as a hypothesis testing problem. The task is to discover "important" features by testing whether the model prediction is significantly different from what would be expected if the features were replaced with randomly-sampled counterfactuals. We derive a multiple hypothesis testing framework for finding important features that enables control over the false discovery rate. We propose two testing methods, as well as analogs of one-sided and two-sided tests. In simulation, the methods have high power and compare favorably against existing interpretability methods. When applied to vision and language models, the framework selects features that intuitively explain model predictions.
Black Box FDR
Jun 08, 2018

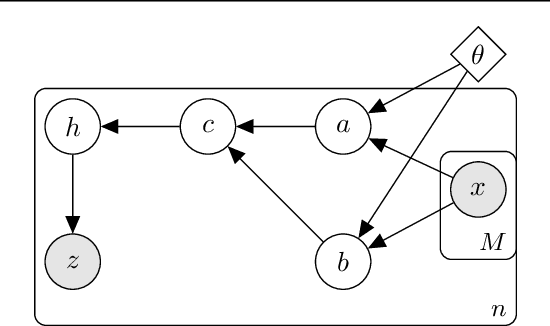
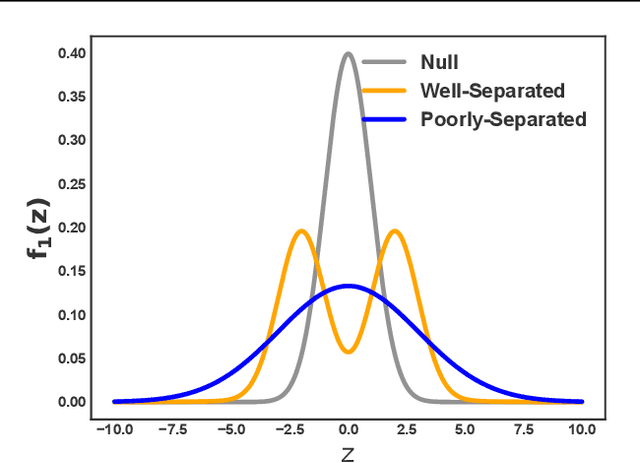
Abstract:Analyzing large-scale, multi-experiment studies requires scientists to test each experimental outcome for statistical significance and then assess the results as a whole. We present Black Box FDR (BB-FDR), an empirical-Bayes method for analyzing multi-experiment studies when many covariates are gathered per experiment. BB-FDR learns a series of black box predictive models to boost power and control the false discovery rate (FDR) at two stages of study analysis. In Stage 1, it uses a deep neural network prior to report which experiments yielded significant outcomes. In Stage 2, a separate black box model of each covariate is used to select features that have significant predictive power across all experiments. In benchmarks, BB-FDR outperforms competing state-of-the-art methods in both stages of analysis. We apply BB-FDR to two real studies on cancer drug efficacy. For both studies, BB-FDR increases the proportion of significant outcomes discovered and selects variables that reveal key genomic drivers of drug sensitivity and resistance in cancer.
Interpretable Low-Dimensional Regression via Data-Adaptive Smoothing
Aug 06, 2017

Abstract:We consider the problem of estimating a regression function in the common situation where the number of features is small, where interpretability of the model is a high priority, and where simple linear or additive models fail to provide adequate performance. To address this problem, we present Maximum Variance Total Variation denoising (MVTV), an approach that is conceptually related both to CART and to the more recent CRISP algorithm, a state-of-the-art alternative method for interpretable nonlinear regression. MVTV divides the feature space into blocks of constant value and fits the value of all blocks jointly via a convex optimization routine. Our method is fully data-adaptive, in that it incorporates highly robust routines for tuning all hyperparameters automatically. We compare our approach against CART and CRISP via both a complexity-accuracy tradeoff metric and a human study, demonstrating that that MVTV is a more powerful and interpretable method.
Deep Nonparametric Estimation of Discrete Conditional Distributions via Smoothed Dyadic Partitioning
Feb 28, 2017



Abstract:We present an approach to deep estimation of discrete conditional probability distributions. Such models have several applications, including generative modeling of audio, image, and video data. Our approach combines two main techniques: dyadic partitioning and graph-based smoothing of the discrete space. By recursively decomposing each dimension into a series of binary splits and smoothing over the resulting distribution using graph-based trend filtering, we impose a strict structure to the model and achieve much higher sample efficiency. We demonstrate the advantages of our model through a series of benchmarks on both synthetic and real-world datasets, in some cases reducing the error by nearly half in comparison to other popular methods in the literature. All of our models are implemented in Tensorflow and publicly available at https://github.com/tansey/sdp .
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge