Christopher Tosh
Optimal rates for density and mode estimation with expand-and-sparsify representations
Feb 05, 2026Abstract:Expand-and-sparsify representations are a class of theoretical models that capture sparse representation phenomena observed in the sensory systems of many animals. At a high level, these representations map an input $x \in \mathbb{R}^d$ to a much higher dimension $m \gg d$ via random linear projections before zeroing out all but the $k \ll m$ largest entries. The result is a $k$-sparse vector in $\{0,1\}^m$. We study the suitability of this representation for two fundamental statistical problems: density estimation and mode estimation. For density estimation, we show that a simple linear function of the expand-and-sparsify representation produces an estimator with minimax-optimal $\ell_{\infty}$ convergence rates. In mode estimation, we provide simple algorithms on top of our density estimator that recover single or multiple modes at optimal rates up to logarithmic factors under mild conditions.
Addressing the Cold-Start Problem for Personalized Combination Drug Screening
Sep 09, 2025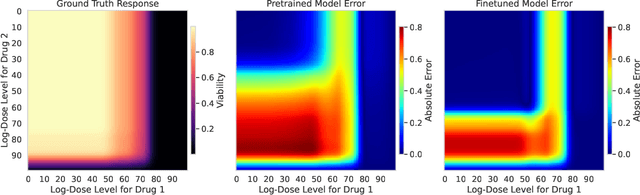
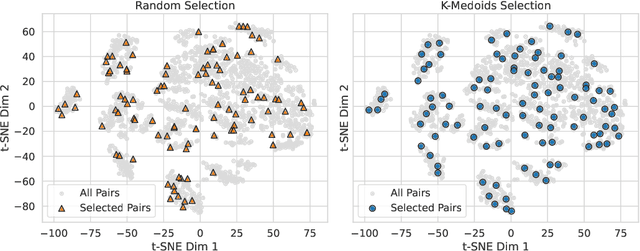
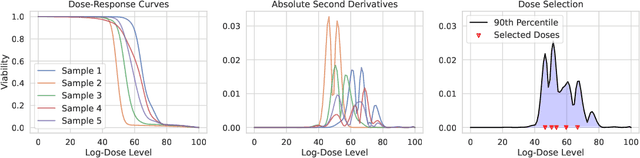
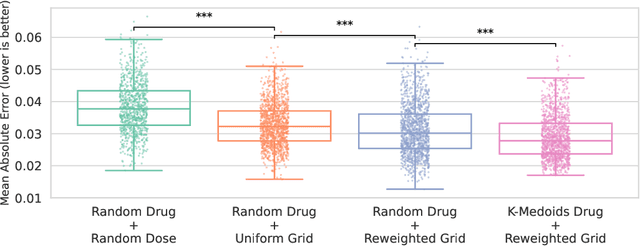
Abstract:Personalizing combination therapies in oncology requires navigating an immense space of possible drug and dose combinations, a task that remains largely infeasible through exhaustive experimentation. Recent developments in patient-derived models have enabled high-throughput ex vivo screening, but the number of feasible experiments is limited. Further, a tight therapeutic window makes gathering molecular profiling information (e.g. RNA-seq) impractical as a means of guiding drug response prediction. This leads to a challenging cold-start problem: how do we select the most informative combinations to test early, when no prior information about the patient is available? We propose a strategy that leverages a pretrained deep learning model built on historical drug response data. The model provides both embeddings for drug combinations and dose-level importance scores, enabling a principled selection of initial experiments. We combine clustering of drug embeddings to ensure functional diversity with a dose-weighting mechanism that prioritizes doses based on their historical informativeness. Retrospective simulations on large-scale drug combination datasets show that our method substantially improves initial screening efficiency compared to baselines, offering a viable path for more effective early-phase decision-making in personalized combination drug screens.
Treatment response as a latent variable
Feb 12, 2025Abstract:Scientists often need to analyze the samples in a study that responded to treatment in order to refine their hypotheses and find potential causal drivers of response. Natural variation in outcomes makes teasing apart responders from non-responders a statistical inference problem. To handle latent responses, we introduce the causal two-groups (C2G) model, a causal extension of the classical two-groups model. The C2G model posits that treated samples may or may not experience an effect, according to some prior probability. We propose two empirical Bayes procedures for the causal two-groups model, one under semi-parametric conditions and another under fully nonparametric conditions. The semi-parametric model assumes additive treatment effects and is identifiable from observed data. The nonparametric model is unidentifiable, but we show it can still be used to test for response in each treated sample. We show empirically and theoretically that both methods for selecting responders control the false discovery rate at the target level with near-optimal power. We also propose two novel estimands of interest and provide a strategy for deriving estimand intervals in the unidentifiable nonparametric model. On a cancer immunotherapy dataset, the nonparametric C2G model recovers clinically-validated predictive biomarkers of both positive and negative outcomes. Code is available at https://github.com/tansey-lab/causal2groups.
Simple and near-optimal algorithms for hidden stratification and multi-group learning
Dec 22, 2021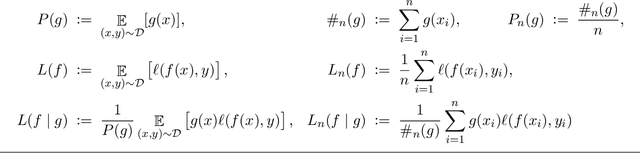
Abstract:Multi-group agnostic learning is a formal learning criterion that is concerned with the conditional risks of predictors within subgroups of a population. The criterion addresses recent practical concerns such as subgroup fairness and hidden stratification. This paper studies the structure of solutions to the multi-group learning problem, and provides simple and near-optimal algorithms for the learning problem.
Bayesian decision-making under misspecified priors with applications to meta-learning
Jul 03, 2021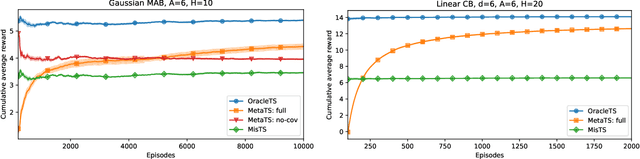
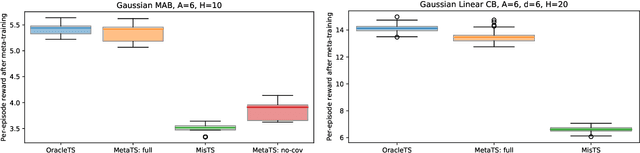
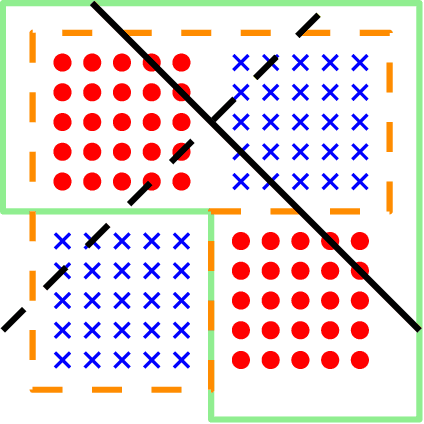
Abstract:Thompson sampling and other Bayesian sequential decision-making algorithms are among the most popular approaches to tackle explore/exploit trade-offs in (contextual) bandits. The choice of prior in these algorithms offers flexibility to encode domain knowledge but can also lead to poor performance when misspecified. In this paper, we demonstrate that performance degrades gracefully with misspecification. We prove that the expected reward accrued by Thompson sampling (TS) with a misspecified prior differs by at most $\tilde{\mathcal{O}}(H^2 \epsilon)$ from TS with a well specified prior, where $\epsilon$ is the total-variation distance between priors and $H$ is the learning horizon. Our bound does not require the prior to have any parametric form. For priors with bounded support, our bound is independent of the cardinality or structure of the action space, and we show that it is tight up to universal constants in the worst case. Building on our sensitivity analysis, we establish generic PAC guarantees for algorithms in the recently studied Bayesian meta-learning setting and derive corollaries for various families of priors. Our results generalize along two axes: (1) they apply to a broader family of Bayesian decision-making algorithms, including a Monte-Carlo implementation of the knowledge gradient algorithm (KG), and (2) they apply to Bayesian POMDPs, the most general Bayesian decision-making setting, encompassing contextual bandits as a special case. Through numerical simulations, we illustrate how prior misspecification and the deployment of one-step look-ahead (as in KG) can impact the convergence of meta-learning in multi-armed and contextual bandits with structured and correlated priors.
Contrastive learning, multi-view redundancy, and linear models
Aug 24, 2020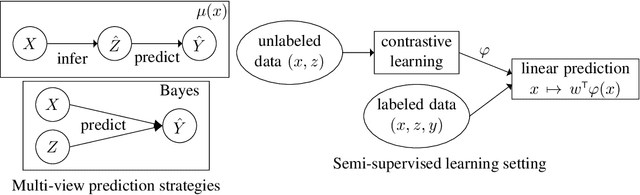
Abstract:Self-supervised learning is an empirically successful approach to unsupervised learning based on creating artificial supervised learning problems. A popular self-supervised approach to representation learning is contrastive learning, which leverages naturally occurring pairs of similar and dissimilar data points, or multiple views of the same data. This work provides a theoretical analysis of contrastive learning in the multi-view setting, where two views of each datum are available. The main result is that linear functions of the learned representations are nearly optimal on downstream prediction tasks whenever the two views provide redundant information about the label.
Expressivity of expand-and-sparsify representations
Jun 05, 2020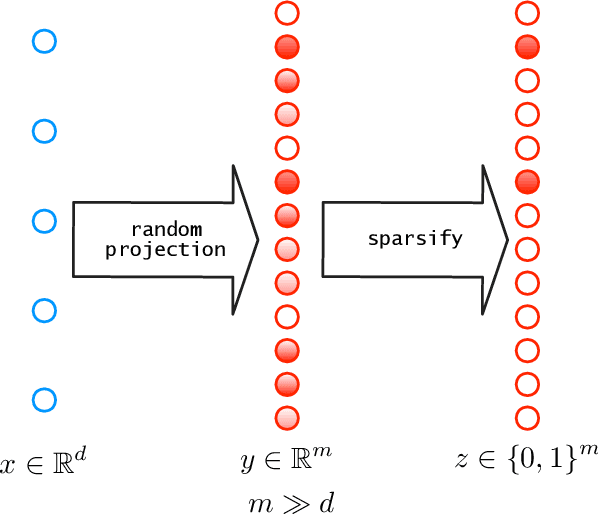
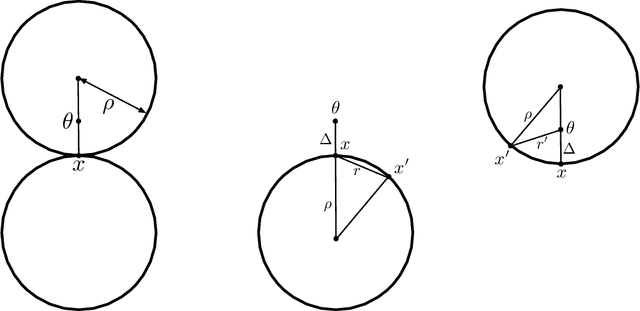
Abstract:A simple sparse coding mechanism appears in the sensory systems of several organisms: to a coarse approximation, an input $x \in \R^d$ is mapped to much higher dimension $m \gg d$ by a random linear transformation, and is then sparsified by a winner-take-all process in which only the positions of the top $k$ values are retained, yielding a $k$-sparse vector $z \in \{0,1\}^m$. We study the benefits of this representation for subsequent learning. We first show a universal approximation property, that arbitrary continuous functions of $x$ are well approximated by linear functions of $z$, provided $m$ is large enough. This can be interpreted as saying that $z$ unpacks the information in $x$ and makes it more readily accessible. The linear functions can be specified explicitly and are easy to learn, and we give bounds on how large $m$ needs to be as a function of the input dimension $d$ and the smoothness of the target function. Next, we consider whether the representation is adaptive to manifold structure in the input space. This is highly dependent on the specific method of sparsification: we show that adaptivity is not obtained under the winner-take-all mechanism, but does hold under a slight variant. Finally we consider mappings to the representation space that are random but are attuned to the data distribution, and we give favorable approximation bounds in this setting.
Contrastive estimation reveals topic posterior information to linear models
Mar 04, 2020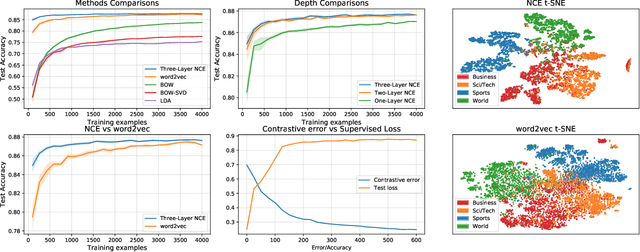
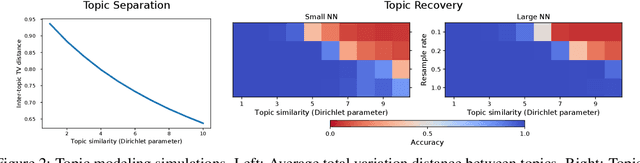
Abstract:Contrastive learning is an approach to representation learning that utilizes naturally occurring similar and dissimilar pairs of data points to find useful embeddings of data. In the context of document classification under topic modeling assumptions, we prove that contrastive learning is capable of recovering a representation of documents that reveals their underlying topic posterior information to linear models. We apply this procedure in a semi-supervised setup and demonstrate empirically that linear classifiers with these representations perform well in document classification tasks with very few training examples.
Interactive Topic Modeling with Anchor Words
Jun 18, 2019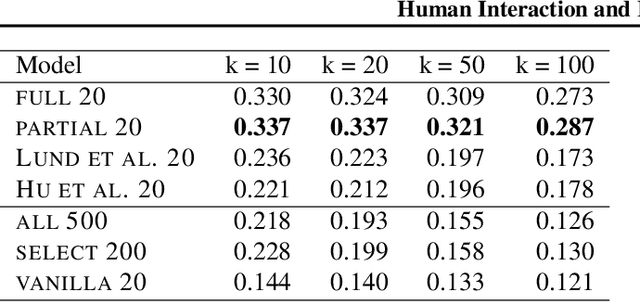
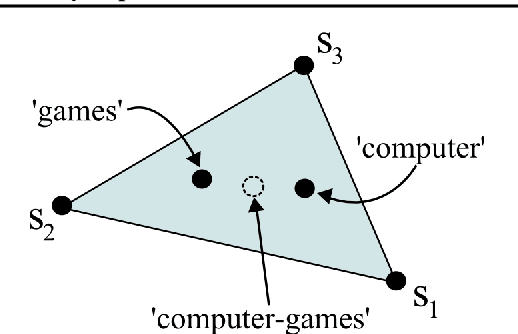


Abstract:The formalism of anchor words has enabled the development of fast topic modeling algorithms with provable guarantees. In this paper, we introduce a protocol that allows users to interact with anchor words to build customized and interpretable topic models. Experimental evidence validating the usefulness of our approach is also presented.
Bayesian Tensor Filtering: Smooth, Locally-Adaptive Factorization of Functional Matrices
Jun 10, 2019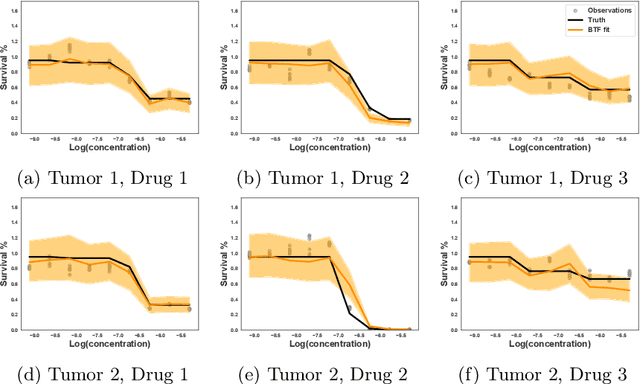

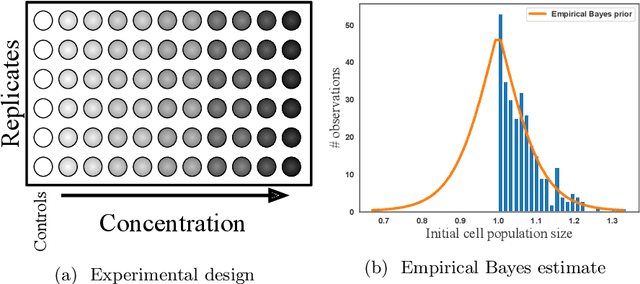
Abstract:We consider the problem of functional matrix factorization, finding low-dimensional structure in a matrix where every entry is a noisy function evaluated at a set of discrete points. Such problems arise frequently in drug discovery, where biological samples form the rows, candidate drugs form the columns, and entries contain the dose-response curve of a sample treated at different concentrations of a drug. We propose Bayesian Tensor Filtering (BTF), a hierarchical Bayesian model of matrices of functions. BTF captures the smoothness in each individual function while also being locally adaptive to sharp discontinuities. The BTF model is agnostic to the likelihood of the underlying observations, making it flexible enough to handle many different kinds of data. We derive efficient Gibbs samplers for three classes of likelihoods: (i) Gaussian, for which updates are fully conjugate; (ii) Binomial and related likelihoods, for which updates are conditionally conjugate through P{\'o}lya--Gamma augmentation; and (iii) Black-box likelihoods, for which updates are non-conjugate but admit an analytic truncated elliptical slice sampling routine. We compare BTF against a state-of-the-art method for dynamic Poisson matrix factorization, showing BTF better reconstructs held out data in synthetic experiments. Finally, we build a dose-response model around BTF and show on real data from a multi-sample, multi-drug cancer study that BTF outperforms the current standard approach in biology. Code for BTF is available at https://github.com/tansey/functionalmf.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge