Expressivity of expand-and-sparsify representations
Paper and Code
Jun 05, 2020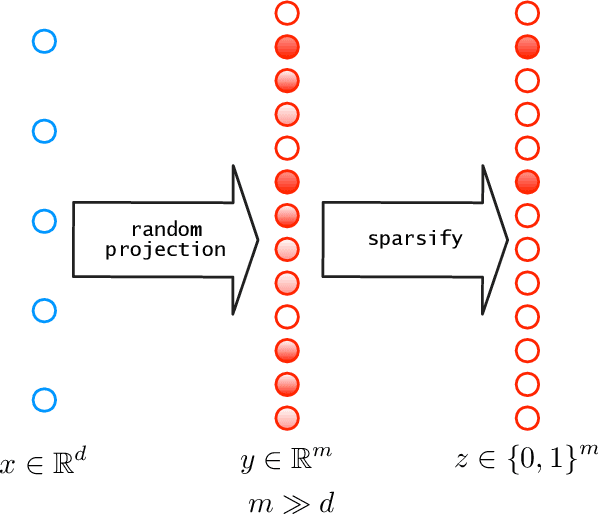
A simple sparse coding mechanism appears in the sensory systems of several organisms: to a coarse approximation, an input $x \in \R^d$ is mapped to much higher dimension $m \gg d$ by a random linear transformation, and is then sparsified by a winner-take-all process in which only the positions of the top $k$ values are retained, yielding a $k$-sparse vector $z \in \{0,1\}^m$. We study the benefits of this representation for subsequent learning. We first show a universal approximation property, that arbitrary continuous functions of $x$ are well approximated by linear functions of $z$, provided $m$ is large enough. This can be interpreted as saying that $z$ unpacks the information in $x$ and makes it more readily accessible. The linear functions can be specified explicitly and are easy to learn, and we give bounds on how large $m$ needs to be as a function of the input dimension $d$ and the smoothness of the target function. Next, we consider whether the representation is adaptive to manifold structure in the input space. This is highly dependent on the specific method of sparsification: we show that adaptivity is not obtained under the winner-take-all mechanism, but does hold under a slight variant. Finally we consider mappings to the representation space that are random but are attuned to the data distribution, and we give favorable approximation bounds in this setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge