Learnability with Partial Labels and Adaptive Nearest Neighbors

Prior work on partial labels learning (PLL) has shown that learning is possible even when each instance is associated with a bag of labels, rather than a single accurate but costly label. However, the necessary conditions for learning with partial labels remain unclear, and existing PLL methods are effective only in specific scenarios. In this work, we mathematically characterize the settings in which PLL is feasible. In addition, we present PL A-$k$NN, an adaptive nearest-neighbors algorithm for PLL that is effective in general scenarios and enjoys strong performance guarantees. Experimental results corroborate that PL A-$k$NN can outperform state-of-the-art methods in general PLL scenarios.

Low-Precision Streaming PCA

Low-precision streaming PCA estimates the top principal component in a streaming setting under limited precision. We establish an information-theoretic lower bound on the quantization resolution required to achieve a target accuracy for the leading eigenvector. We study Oja's algorithm for streaming PCA under linear and nonlinear stochastic quantization. The quantized variants use unbiased stochastic quantization of the weight vector and the updates. Under mild moment and spectral-gap assumptions on the data distribution, we show that a batched version achieves the lower bound up to logarithmic factors under both schemes. This leads to a nearly dimension-free quantization error in the nonlinear quantization setting. Empirical evaluations on synthetic streams validate our theoretical findings and demonstrate that our low-precision methods closely track the performance of standard Oja's algorithm.

Reliable Programmatic Weak Supervision with Confidence Intervals for Label Probabilities

The accurate labeling of datasets is often both costly and time-consuming. Given an unlabeled dataset, programmatic weak supervision obtains probabilistic predictions for the labels by leveraging multiple weak labeling functions (LFs) that provide rough guesses for labels. Weak LFs commonly provide guesses with assorted types and unknown interdependences that can result in unreliable predictions. Furthermore, existing techniques for programmatic weak supervision cannot provide assessments for the reliability of the probabilistic predictions for labels. This paper presents a methodology for programmatic weak supervision that can provide confidence intervals for label probabilities and obtain more reliable predictions. In particular, the methods proposed use uncertainty sets of distributions that encapsulate the information provided by LFs with unrestricted behavior and typology. Experiments on multiple benchmark datasets show the improvement of the presented methods over the state-of-the-art and the practicality of the confidence intervals presented.

Graph neural networks extrapolate out-of-distribution for shortest paths

Neural networks (NNs), despite their success and wide adoption, still struggle to extrapolate out-of-distribution (OOD), i.e., to inputs that are not well-represented by their training dataset. Addressing the OOD generalization gap is crucial when models are deployed in environments significantly different from the training set, such as applying Graph Neural Networks (GNNs) trained on small graphs to large, real-world graphs. One promising approach for achieving robust OOD generalization is the framework of neural algorithmic alignment, which incorporates ideas from classical algorithms by designing neural architectures that resemble specific algorithmic paradigms (e.g. dynamic programming). The hope is that trained models of this form would have superior OOD capabilities, in much the same way that classical algorithms work for all instances. We rigorously analyze the role of algorithmic alignment in achieving OOD generalization, focusing on graph neural networks (GNNs) applied to the canonical shortest path problem. We prove that GNNs, trained to minimize a sparsity-regularized loss over a small set of shortest path instances, exactly implement the Bellman-Ford (BF) algorithm for shortest paths. In fact, if a GNN minimizes this loss within an error of $\epsilon$, it implements the BF algorithm with an error of $O(\epsilon)$. Consequently, despite limited training data, these GNNs are guaranteed to extrapolate to arbitrary shortest-path problems, including instances of any size. Our empirical results support our theory by showing that NNs trained by gradient descent are able to minimize this loss and extrapolate in practice.

Learning Smooth Distance Functions via Queries

In this work, we investigate the problem of learning distance functions within the query-based learning framework, where a learner is able to pose triplet queries of the form: ``Is $x_i$ closer to $x_j$ or $x_k$?'' We establish formal guarantees on the query complexity required to learn smooth, but otherwise general, distance functions under two notions of approximation: $\omega$-additive approximation and $(1 + \omega)$-multiplicative approximation. For the additive approximation, we propose a global method whose query complexity is quadratic in the size of a finite cover of the sample space. For the (stronger) multiplicative approximation, we introduce a method that combines global and local approaches, utilizing multiple Mahalanobis distance functions to capture local geometry. This method has a query complexity that scales quadratically with both the size of the cover and the ambient space dimension of the sample space.

Online Consistency of the Nearest Neighbor Rule

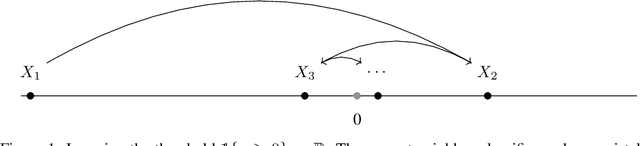
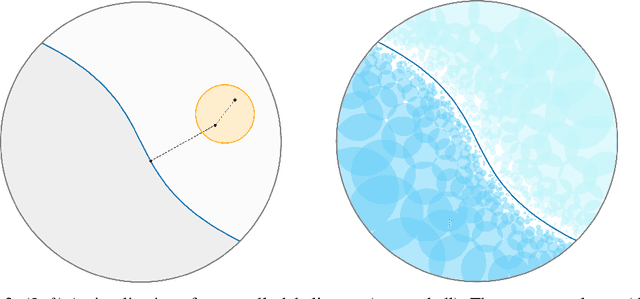
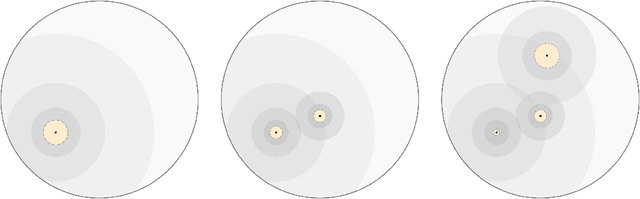
In the realizable online setting, a learner is tasked with making predictions for a stream of instances, where the correct answer is revealed after each prediction. A learning rule is online consistent if its mistake rate eventually vanishes. The nearest neighbor rule (Fix and Hodges, 1951) is a fundamental prediction strategy, but it is only known to be consistent under strong statistical or geometric assumptions: the instances come i.i.d. or the label classes are well-separated. We prove online consistency for all measurable functions in doubling metric spaces under the mild assumption that the instances are generated by a process that is uniformly absolutely continuous with respect to a finite, upper doubling measure.

Convergence Behavior of an Adversarial Weak Supervision Method

Labeling data via rules-of-thumb and minimal label supervision is central to Weak Supervision, a paradigm subsuming subareas of machine learning such as crowdsourced learning and semi-supervised ensemble learning. By using this labeled data to train modern machine learning methods, the cost of acquiring large amounts of hand labeled data can be ameliorated. Approaches to combining the rules-of-thumb falls into two camps, reflecting different ideologies of statistical estimation. The most common approach, exemplified by the Dawid-Skene model, is based on probabilistic modeling. The other, developed in the work of Balsubramani-Freund and others, is adversarial and game-theoretic. We provide a variety of statistical results for the adversarial approach under log-loss: we characterize the form of the solution, relate it to logistic regression, demonstrate consistency, and give rates of convergence. On the other hand, we find that probabilistic approaches for the same model class can fail to be consistent. Experimental results are provided to corroborate the theoretical results.

New bounds on the cohesion of complete-link and other linkage methods for agglomeration clustering

Linkage methods are among the most popular algorithms for hierarchical clustering. Despite their relevance the current knowledge regarding the quality of the clustering produced by these methods is limited. Here, we improve the currently available bounds on the maximum diameter of the clustering obtained by complete-link for metric spaces. One of our new bounds, in contrast to the existing ones, allows us to separate complete-link from single-link in terms of approximation for the diameter, which corroborates the common perception that the former is more suitable than the latter when the goal is producing compact clusters. We also show that our techniques can be employed to derive upper bounds on the cohesion of a class of linkage methods that includes the quite popular average-link.

Online nearest neighbor classification

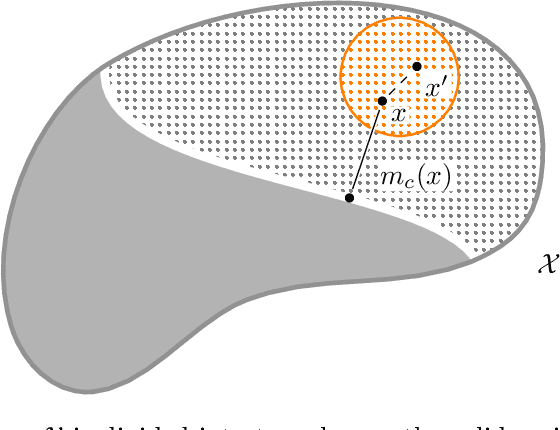
We study an instance of online non-parametric classification in the realizable setting. In particular, we consider the classical 1-nearest neighbor algorithm, and show that it achieves sublinear regret - that is, a vanishing mistake rate - against dominated or smoothed adversaries in the realizable setting.

Active learning using region-based sampling

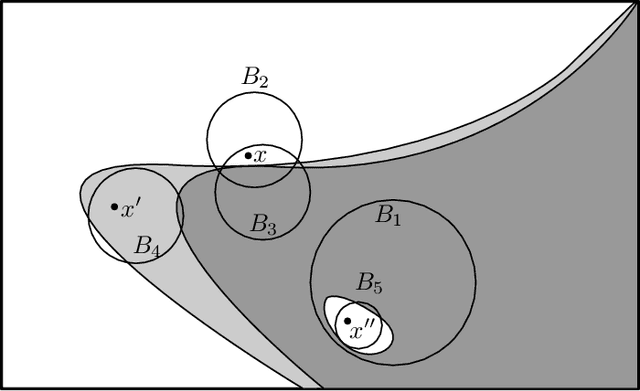
We present a general-purpose active learning scheme for data in metric spaces. The algorithm maintains a collection of neighborhoods of different sizes and uses label queries to identify those that have a strong bias towards one particular label; when two such neighborhoods intersect and have different labels, the region of overlap is treated as a ``known unknown'' and is a target of future active queries. We give label complexity bounds for this method that do not rely on assumptions about the data and we instantiate them in several cases of interest.