Convergence of online $k$-means

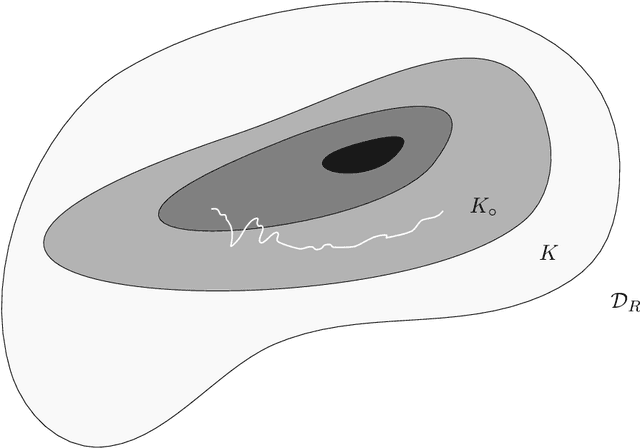
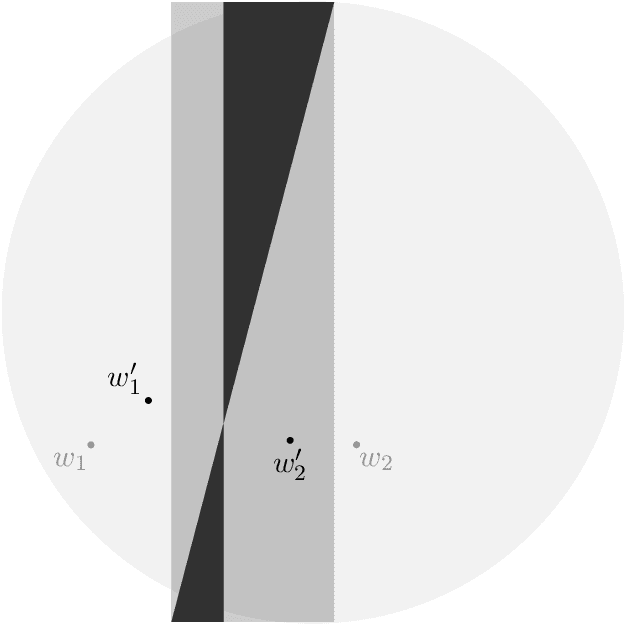
We prove asymptotic convergence for a general class of $k$-means algorithms performed over streaming data from a distribution: the centers asymptotically converge to the set of stationary points of the $k$-means cost function. To do so, we show that online $k$-means over a distribution can be interpreted as stochastic gradient descent with a stochastic learning rate schedule. Then, we prove convergence by extending techniques used in optimization literature to handle settings where center-specific learning rates may depend on the past trajectory of the centers.