Improved classical shadows from local symmetries in the Schur basis

We study the sample complexity of the classical shadows task: what is the fewest number of copies of an unknown state you need to measure to predict expected values with respect to some class of observables? Large joint measurements are likely required in order to minimize sample complexity, but previous joint measurement protocols only work when the unknown state is pure. We present the first joint measurement protocol for classical shadows whose sample complexity scales with the rank of the unknown state. In particular we prove $\mathcal O(\sqrt{rB}/\epsilon^2)$ samples suffice, where $r$ is the rank of the state, $B$ is a bound on the squared Frobenius norm of the observables, and $\epsilon$ is the target accuracy. In the low-rank regime, this is a nearly quadratic advantage over traditional approaches that use single-copy measurements. We present several intermediate results that may be of independent interest: a solution to a new formulation of classical shadows that captures functions of non-identical input states; a generalization of a ``nice'' Schur basis used for optimal qubit purification and quantum majority vote; and a measurement strategy that allows us to use local symmetries in the Schur basis to avoid intractable Weingarten calculations in the analysis.

Learning Hidden Markov Models Using Conditional Samples

This paper is concerned with the computational complexity of learning the Hidden Markov Model (HMM). Although HMMs are some of the most widely used tools in sequential and time series modeling, they are cryptographically hard to learn in the standard setting where one has access to i.i.d. samples of observation sequences. In this paper, we depart from this setup and consider an interactive access model, in which the algorithm can query for samples from the conditional distributions of the HMMs. We show that interactive access to the HMM enables computationally efficient learning algorithms, thereby bypassing cryptographic hardness. Specifically, we obtain efficient algorithms for learning HMMs in two settings: (a) An easier setting where we have query access to the exact conditional probabilities. Here our algorithm runs in polynomial time and makes polynomially many queries to approximate any HMM in total variation distance. (b) A harder setting where we can only obtain samples from the conditional distributions. Here the performance of the algorithm depends on a new parameter, called the fidelity of the HMM. We show that this captures cryptographically hard instances and previously known positive results. We also show that these results extend to a broader class of distributions with latent low rank structure. Our algorithms can be viewed as generalizations and robustifications of Angluin's $L^*$ algorithm for learning deterministic finite automata from membership queries.

Exponential Hardness of Reinforcement Learning with Linear Function Approximation

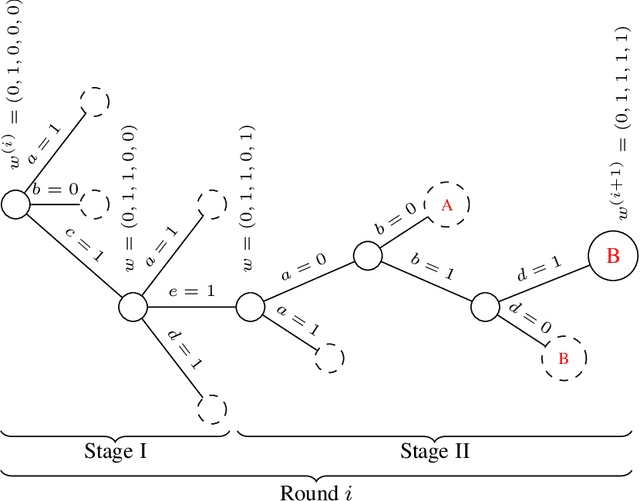
A fundamental question in reinforcement learning theory is: suppose the optimal value functions are linear in given features, can we learn them efficiently? This problem's counterpart in supervised learning, linear regression, can be solved both statistically and computationally efficiently. Therefore, it was quite surprising when a recent work \cite{kane2022computational} showed a computational-statistical gap for linear reinforcement learning: even though there are polynomial sample-complexity algorithms, unless NP = RP, there are no polynomial time algorithms for this setting. In this work, we build on their result to show a computational lower bound, which is exponential in feature dimension and horizon, for linear reinforcement learning under the Randomized Exponential Time Hypothesis. To prove this we build a round-based game where in each round the learner is searching for an unknown vector in a unit hypercube. The rewards in this game are chosen such that if the learner achieves large reward, then the learner's actions can be used to simulate solving a variant of 3-SAT, where (a) each variable shows up in a bounded number of clauses (b) if an instance has no solutions then it also has no solutions that satisfy more than (1-$\epsilon$)-fraction of clauses. We use standard reductions to show this 3-SAT variant is approximately as hard as 3-SAT. Finally, we also show a lower bound optimized for horizon dependence that almost matches the best known upper bound of $\exp(\sqrt{H})$.

Do PAC-Learners Learn the Marginal Distribution?

We study a foundational variant of Valiant and Vapnik and Chervonenkis' Probably Approximately Correct (PAC)-Learning in which the adversary is restricted to a known family of marginal distributions $\mathscr{P}$. In particular, we study how the PAC-learnability of a triple $(\mathscr{P},X,H)$ relates to the learners ability to infer \emph{distributional} information about the adversary's choice of $D \in \mathscr{P}$. To this end, we introduce the `unsupervised' notion of \emph{TV-Learning}, which, given a class $(\mathscr{P},X,H)$, asks the learner to approximate $D$ from unlabeled samples with respect to a natural class-conditional total variation metric. In the classical distribution-free setting, we show that TV-learning is \emph{equivalent} to PAC-Learning: in other words, any learner must infer near-maximal information about $D$. On the other hand, we show this characterization breaks down for general $\mathscr{P}$, where PAC-Learning is strictly sandwiched between two approximate variants we call `Strong' and `Weak' TV-learning, roughly corresponding to unsupervised learners that estimate most relevant distances in $D$ with respect to $H$, but differ in whether the learner \emph{knows} the set of well-estimated events. Finally, we observe that TV-learning is in fact equivalent to the classical notion of \emph{uniform estimation}, and thereby give a strong refutation of the uniform convergence paradigm in supervised learning.

Convergence of online $k$-means

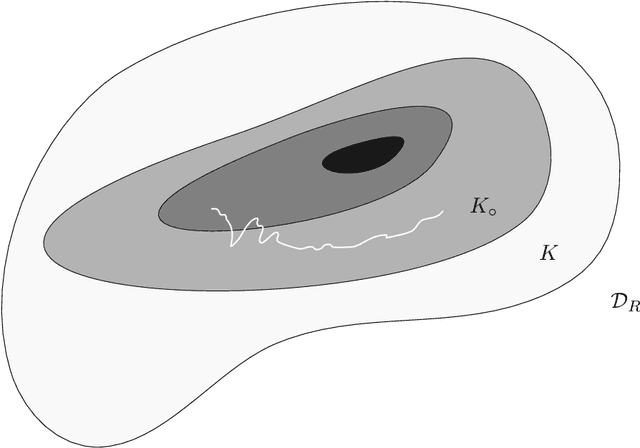
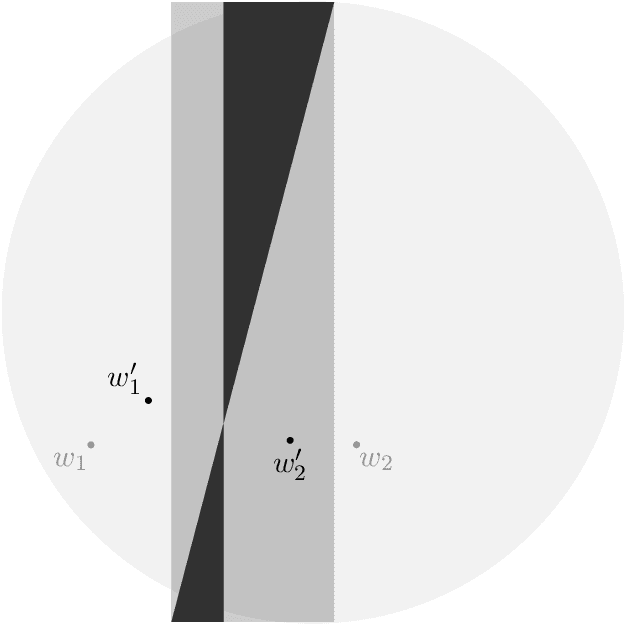
We prove asymptotic convergence for a general class of $k$-means algorithms performed over streaming data from a distribution: the centers asymptotically converge to the set of stationary points of the $k$-means cost function. To do so, we show that online $k$-means over a distribution can be interpreted as stochastic gradient descent with a stochastic learning rate schedule. Then, we prove convergence by extending techniques used in optimization literature to handle settings where center-specific learning rates may depend on the past trajectory of the centers.

Computational-Statistical Gaps in Reinforcement Learning

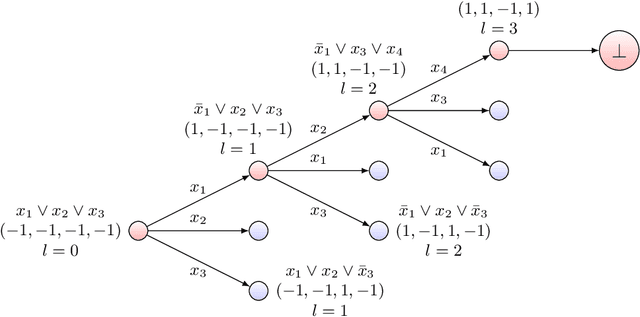
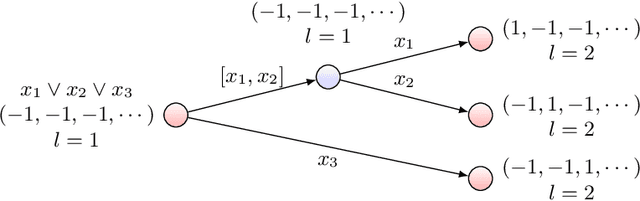
Reinforcement learning with function approximation has recently achieved tremendous results in applications with large state spaces. This empirical success has motivated a growing body of theoretical work proposing necessary and sufficient conditions under which efficient reinforcement learning is possible. From this line of work, a remarkably simple minimal sufficient condition has emerged for sample efficient reinforcement learning: MDPs with optimal value function $V^*$ and $Q^*$ linear in some known low-dimensional features. In this setting, recent works have designed sample efficient algorithms which require a number of samples polynomial in the feature dimension and independent of the size of state space. They however leave finding computationally efficient algorithms as future work and this is considered a major open problem in the community. In this work, we make progress on this open problem by presenting the first computational lower bound for RL with linear function approximation: unless NP=RP, no randomized polynomial time algorithm exists for deterministic transition MDPs with a constant number of actions and linear optimal value functions. To prove this, we show a reduction from Unique-Sat, where we convert a CNF formula into an MDP with deterministic transitions, constant number of actions and low dimensional linear optimal value functions. This result also exhibits the first computational-statistical gap in reinforcement learning with linear function approximation, as the underlying statistical problem is information-theoretically solvable with a polynomial number of queries, but no computationally efficient algorithm exists unless NP=RP. Finally, we also prove a quasi-polynomial time lower bound under the Randomized Exponential Time Hypothesis.

Learning what to remember

We consider a lifelong learning scenario in which a learner faces a neverending and arbitrary stream of facts and has to decide which ones to retain in its limited memory. We introduce a mathematical model based on the online learning framework, in which the learner measures itself against a collection of experts that are also memory-constrained and that reflect different policies for what to remember. Interspersed with the stream of facts are occasional questions, and on each of these the learner incurs a loss if it has not remembered the corresponding fact. Its goal is to do almost as well as the best expert in hindsight, while using roughly the same amount of memory. We identify difficulties with using the multiplicative weights update algorithm in this memory-constrained scenario, and design an alternative scheme whose regret guarantees are close to the best possible.

Realizable Learning is All You Need

The equivalence of realizable and agnostic learnability is a fundamental phenomenon in learning theory. With variants ranging from classical settings like PAC learning and regression to recent trends such as adversarially robust and private learning, it's surprising that we still lack a unified theory; traditional proofs of the equivalence tend to be disparate, and rely on strong model-specific assumptions like uniform convergence and sample compression. In this work, we give the first model-independent framework explaining the equivalence of realizable and agnostic learnability: a three-line blackbox reduction that simplifies, unifies, and extends our understanding across a wide variety of settings. This includes models with no known characterization of learnability such as learning with arbitrary distributional assumptions or general loss, as well as a host of other popular settings such as robust learning, partial learning, fair learning, and the statistical query model. More generally, we argue that the equivalence of realizable and agnostic learning is actually a special case of a broader phenomenon we call property generalization: any desirable property of a learning algorithm (e.g.\ noise tolerance, privacy, stability) that can be satisfied over finite hypothesis classes extends (possibly in some variation) to any learnable hypothesis class.

Bilinear Classes: A Structural Framework for Provable Generalization in RL

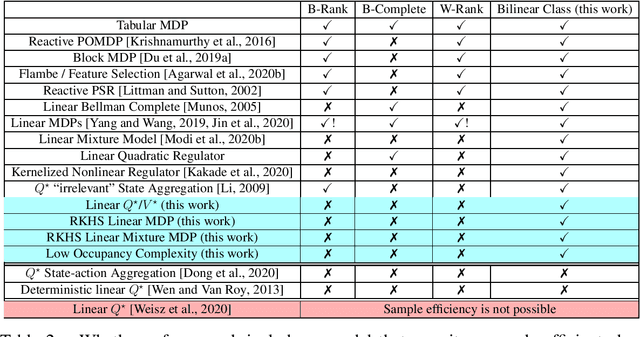
This work introduces Bilinear Classes, a new structural framework, which permit generalization in reinforcement learning in a wide variety of settings through the use of function approximation. The framework incorporates nearly all existing models in which a polynomial sample complexity is achievable, and, notably, also includes new models, such as the Linear $Q^*/V^*$ model in which both the optimal $Q$-function and the optimal $V$-function are linear in some known feature space. Our main result provides an RL algorithm which has polynomial sample complexity for Bilinear Classes; notably, this sample complexity is stated in terms of a reduction to the generalization error of an underlying supervised learning sub-problem. These bounds nearly match the best known sample complexity bounds for existing models. Furthermore, this framework also extends to the infinite dimensional (RKHS) setting: for the the Linear $Q^*/V^*$ model, linear MDPs, and linear mixture MDPs, we provide sample complexities that have no explicit dependence on the explicit feature dimension (which could be infinite), but instead depends only on information theoretic quantities.

Point Location and Active Learning: Learning Halfspaces Almost Optimally

Given a finite set $X \subset \mathbb{R}^d$ and a binary linear classifier $c: \mathbb{R}^d \to \{0,1\}$, how many queries of the form $c(x)$ are required to learn the label of every point in $X$? Known as \textit{point location}, this problem has inspired over 35 years of research in the pursuit of an optimal algorithm. Building on the prior work of Kane, Lovett, and Moran (ICALP 2018), we provide the first nearly optimal solution, a randomized linear decision tree of depth $\tilde{O}(d\log(|X|))$, improving on the previous best of $\tilde{O}(d^2\log(|X|))$ from Ezra and Sharir (Discrete and Computational Geometry, 2019). As a corollary, we also provide the first nearly optimal algorithm for actively learning halfspaces in the membership query model. En route to these results, we prove a novel characterization of Barthe's Theorem (Inventiones Mathematicae, 1998) of independent interest. In particular, we show that $X$ may be transformed into approximate isotropic position if and only if there exists no $k$-dimensional subspace with more than a $k/d$-fraction of $X$, and provide a similar characterization for exact isotropic position.