Online Consistency of the Nearest Neighbor Rule

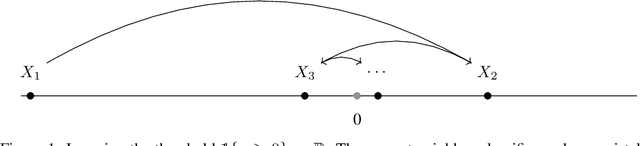
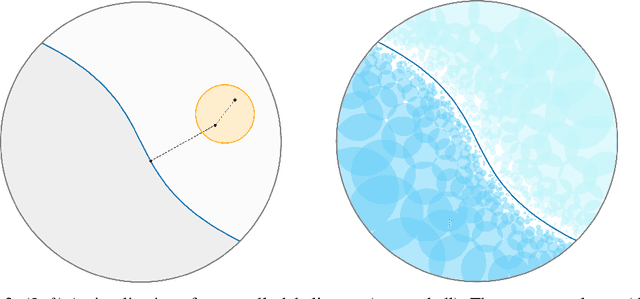
In the realizable online setting, a learner is tasked with making predictions for a stream of instances, where the correct answer is revealed after each prediction. A learning rule is online consistent if its mistake rate eventually vanishes. The nearest neighbor rule (Fix and Hodges, 1951) is a fundamental prediction strategy, but it is only known to be consistent under strong statistical or geometric assumptions: the instances come i.i.d. or the label classes are well-separated. We prove online consistency for all measurable functions in doubling metric spaces under the mild assumption that the instances are generated by a process that is uniformly absolutely continuous with respect to a finite, upper doubling measure.

Metric Learning from Limited Pairwise Preference Comparisons

We study metric learning from preference comparisons under the ideal point model, in which a user prefers an item over another if it is closer to their latent ideal item. These items are embedded into $\mathbb{R}^d$ equipped with an unknown Mahalanobis distance shared across users. While recent work shows that it is possible to simultaneously recover the metric and ideal items given $\mathcal{O}(d)$ pairwise comparisons per user, in practice we often have a limited budget of $o(d)$ comparisons. We study whether the metric can still be recovered, even though it is known that learning individual ideal items is now no longer possible. We show that in general, $o(d)$ comparisons reveals no information about the metric, even with infinitely many users. However, when comparisons are made over items that exhibit low-dimensional structure, each user can contribute to learning the metric restricted to a low-dimensional subspace so that the metric can be jointly identified. We present a divide-and-conquer approach that achieves this, and provide theoretical recovery guarantees and empirical validation.

Optimization on Pareto sets: On a theory of multi-objective optimization

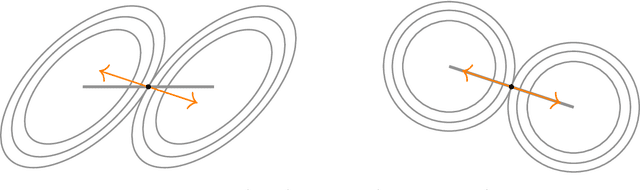
In multi-objective optimization, a single decision vector must balance the trade-offs between many objectives. Solutions achieving an optimal trade-off are said to be Pareto optimal: these are decision vectors for which improving any one objective must come at a cost to another. But as the set of Pareto optimal vectors can be very large, we further consider a more practically significant Pareto-constrained optimization problem, where the goal is to optimize a preference function constrained to the Pareto set. We investigate local methods for solving this constrained optimization problem, which poses significant challenges because the constraint set is (i) implicitly defined, and (ii) generally non-convex and non-smooth, even when the objectives are. We define notions of optimality and stationarity, and provide an algorithm with a last-iterate convergence rate of $O(K^{-1/2})$ to stationarity when the objectives are strongly convex and Lipschitz smooth.

Online nearest neighbor classification

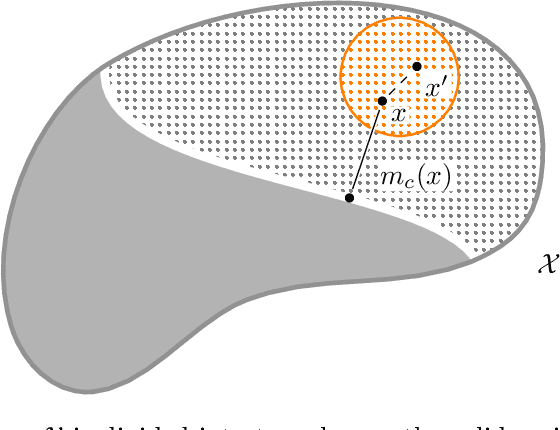
We study an instance of online non-parametric classification in the realizable setting. In particular, we consider the classical 1-nearest neighbor algorithm, and show that it achieves sublinear regret - that is, a vanishing mistake rate - against dominated or smoothed adversaries in the realizable setting.

Convergence of online $k$-means

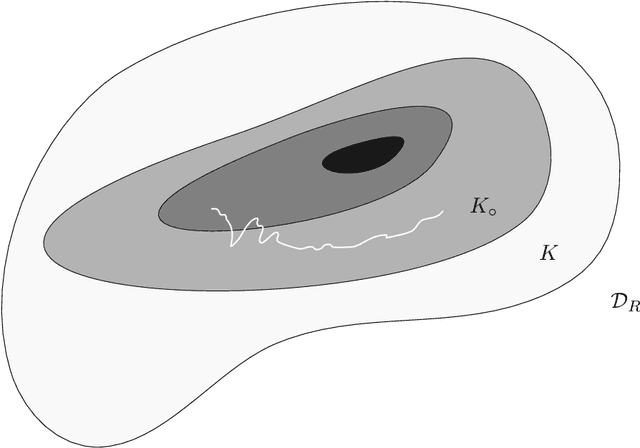
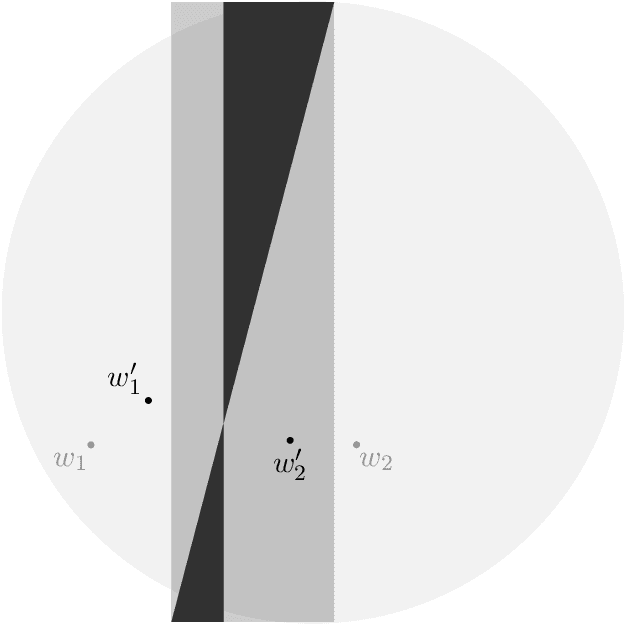
We prove asymptotic convergence for a general class of $k$-means algorithms performed over streaming data from a distribution: the centers asymptotically converge to the set of stationary points of the $k$-means cost function. To do so, we show that online $k$-means over a distribution can be interpreted as stochastic gradient descent with a stochastic learning rate schedule. Then, we prove convergence by extending techniques used in optimization literature to handle settings where center-specific learning rates may depend on the past trajectory of the centers.