LaDiR: Latent Diffusion Enhances LLMs for Text Reasoning

Large Language Models (LLMs) demonstrate their reasoning ability through chain-of-thought (CoT) generation. However, LLM's autoregressive decoding may limit the ability to revisit and refine earlier tokens in a holistic manner, which can also lead to inefficient exploration for diverse solutions. In this paper, we propose LaDiR (Latent Diffusion Reasoner), a novel reasoning framework that unifies the expressiveness of continuous latent representation with the iterative refinement capabilities of latent diffusion models for an existing LLM. We first construct a structured latent reasoning space using a Variational Autoencoder (VAE) that encodes text reasoning steps into blocks of thought tokens, preserving semantic information and interpretability while offering compact but expressive representations. Subsequently, we utilize a latent diffusion model that learns to denoise a block of latent thought tokens with a blockwise bidirectional attention mask, enabling longer horizon and iterative refinement with adaptive test-time compute. This design allows efficient parallel generation of diverse reasoning trajectories, allowing the model to plan and revise the reasoning process holistically. We conduct evaluations on a suite of mathematical reasoning and planning benchmarks. Empirical results show that LaDiR consistently improves accuracy, diversity, and interpretability over existing autoregressive, diffusion-based, and latent reasoning methods, revealing a new paradigm for text reasoning with latent diffusion.

Nearly Dimension-Independent Convergence of Mean-Field Black-Box Variational Inference

We prove that, given a mean-field location-scale variational family, black-box variational inference (BBVI) with the reparametrization gradient converges at an almost dimension-independent rate. Specifically, for strongly log-concave and log-smooth targets, the number of iterations for BBVI with a sub-Gaussian family to achieve an objective $\epsilon$-close to the global optimum is $\mathrm{O}(\log d)$, which improves over the $\mathrm{O}(d)$ dependence of full-rank location-scale families. For heavy-tailed families, we provide a weaker $\mathrm{O}(d^{2/k})$ dimension dependence, where $k$ is the number of finite moments. Additionally, if the Hessian of the target log-density is constant, the complexity is free of any explicit dimension dependence. We also prove that our bound on the gradient variance, which is key to our result, cannot be improved using only spectral bounds on the Hessian of the target log-density.

Purifying Approximate Differential Privacy with Randomized Post-processing

We propose a framework to convert $(\varepsilon, \delta)$-approximate Differential Privacy (DP) mechanisms into $(\varepsilon, 0)$-pure DP mechanisms, a process we call ``purification''. This algorithmic technique leverages randomized post-processing with calibrated noise to eliminate the $\delta$ parameter while preserving utility. By combining the tighter utility bounds and computational efficiency of approximate DP mechanisms with the stronger guarantees of pure DP, our approach achieves the best of both worlds. We illustrate the applicability of this framework in various settings, including Differentially Private Empirical Risk Minimization (DP-ERM), data-dependent DP mechanisms such as Propose-Test-Release (PTR), and query release tasks. To the best of our knowledge, this is the first work to provide a systematic method for transforming approximate DP into pure DP while maintaining competitive accuracy and computational efficiency.

Learning to Steer Learners in Games

We consider the problem of learning to exploit learning algorithms through repeated interactions in games. Specifically, we focus on the case of repeated two player, finite-action games, in which an optimizer aims to steer a no-regret learner to a Stackelberg equilibrium without knowledge of its payoffs. We first show that this is impossible if the optimizer only knows that the learner is using an algorithm from the general class of no-regret algorithms. This suggests that the optimizer requires more information about the learner's objectives or algorithm to successfully exploit them. Building on this intuition, we reduce the problem for the optimizer to that of recovering the learner's payoff structure. We demonstrate the effectiveness of this approach if the learner's algorithm is drawn from a smaller class by analyzing two examples: one where the learner uses an ascent algorithm, and another where the learner uses stochastic mirror ascent with known regularizer and step sizes.

Discovering Latent Structural Causal Models from Spatio-Temporal Data

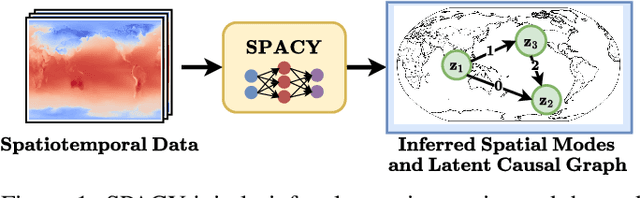
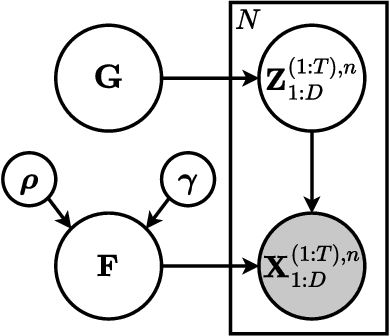
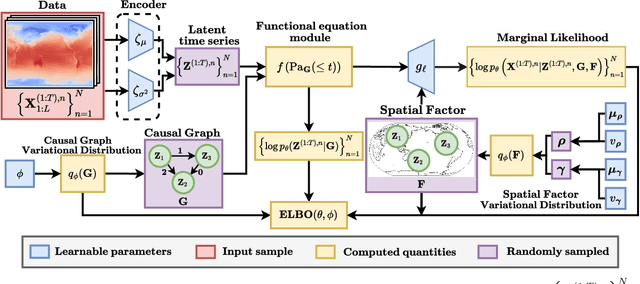
Many important phenomena in scientific fields such as climate, neuroscience, and epidemiology are naturally represented as spatiotemporal gridded data with complex interactions. For example, in climate science, researchers aim to uncover how large-scale events, such as the North Atlantic Oscillation (NAO) and the Antarctic Oscillation (AAO), influence other global processes. Inferring causal relationships from these data is a challenging problem compounded by the high dimensionality of such data and the correlations between spatially proximate points. We present SPACY (SPAtiotemporal Causal discoverY), a novel framework based on variational inference, designed to explicitly model latent time-series and their causal relationships from spatially confined modes in the data. Our method uses an end-to-end training process that maximizes an evidence-lower bound (ELBO) for the data likelihood. Theoretically, we show that, under some conditions, the latent variables are identifiable up to transformation by an invertible matrix. Empirically, we show that SPACY outperforms state-of-the-art baselines on synthetic data, remains scalable for large grids, and identifies key known phenomena from real-world climate data.

Functional-level Uncertainty Quantification for Calibrated Fine-tuning on LLMs

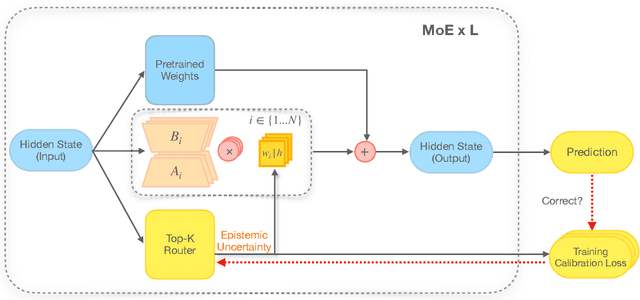
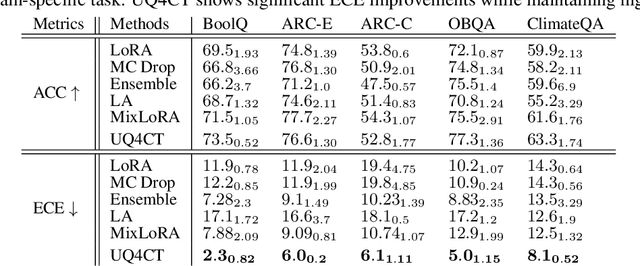
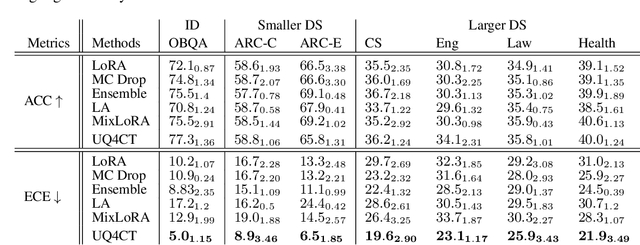
From common-sense reasoning to domain-specific tasks, parameter-efficient fine tuning (PEFT) methods for large language models (LLMs) have showcased significant performance improvements on downstream tasks. However, fine-tuned LLMs often struggle with overconfidence in uncertain predictions, particularly due to sparse training data. This overconfidence reflects poor epistemic uncertainty calibration, which arises from limitations in the model's ability to generalize with limited data. Existing PEFT uncertainty quantification methods for LLMs focus on the post fine-tuning stage and thus have limited capability in calibrating epistemic uncertainty. To address these limitations, we propose Functional-Level Uncertainty Quantification for Calibrated Fine-Tuning (UQ4CT), which captures and calibrates functional-level epistemic uncertainty during the fine-tuning stage via a mixture-of-expert framework. We show that UQ4CT reduces Expected Calibration Error (ECE) by more than $25\%$ while maintaining high accuracy across $5$ benchmarks. Furthermore, UQ4CT maintains superior ECE performance with high accuracy under distribution shift, showcasing improved generalizability.

A Skewness-Based Criterion for Addressing Heteroscedastic Noise in Causal Discovery

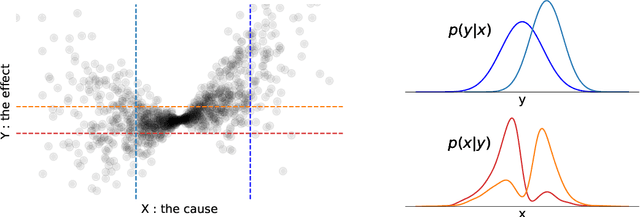
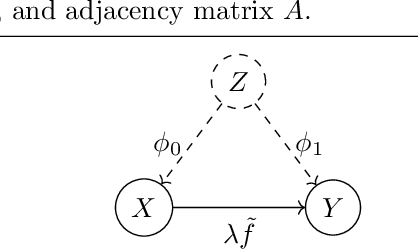
Real-world data often violates the equal-variance assumption (homoscedasticity), making it essential to account for heteroscedastic noise in causal discovery. In this work, we explore heteroscedastic symmetric noise models (HSNMs), where the effect $Y$ is modeled as $Y = f(X) + \sigma(X)N$, with $X$ as the cause and $N$ as independent noise following a symmetric distribution. We introduce a novel criterion for identifying HSNMs based on the skewness of the score (i.e., the gradient of the log density) of the data distribution. This criterion establishes a computationally tractable measurement that is zero in the causal direction but nonzero in the anticausal direction, enabling the causal direction discovery. We extend this skewness-based criterion to the multivariate setting and propose SkewScore, an algorithm that handles heteroscedastic noise without requiring the extraction of exogenous noise. We also conduct a case study on the robustness of SkewScore in a bivariate model with a latent confounder, providing theoretical insights into its performance. Empirical studies further validate the effectiveness of the proposed method.

Log-concave Sampling over a Convex Body with a Barrier: a Robust and Unified Dikin Walk

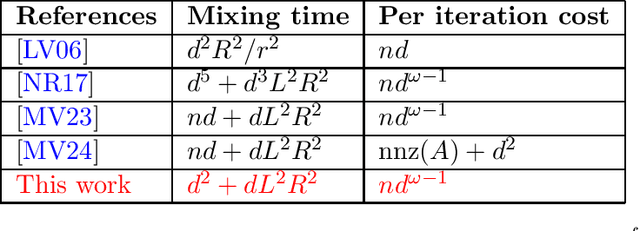
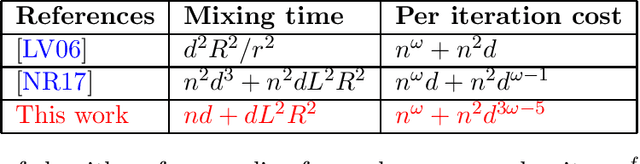
We consider the problem of sampling from a $d$-dimensional log-concave distribution $\pi(\theta) \propto \exp(-f(\theta))$ for $L$-Lipschitz $f$, constrained to a convex body with an efficiently computable self-concordant barrier function, contained in a ball of radius $R$ with a $w$-warm start. We propose a \emph{robust} sampling framework that computes spectral approximations to the Hessian of the barrier functions in each iteration. We prove that for polytopes that are described by $n$ hyperplanes, sampling with the Lee-Sidford barrier function mixes within $\widetilde O((d^2+dL^2R^2)\log(w/\delta))$ steps with a per step cost of $\widetilde O(nd^{\omega-1})$, where $\omega\approx 2.37$ is the fast matrix multiplication exponent. Compared to the prior work of Mangoubi and Vishnoi, our approach gives faster mixing time as we are able to design a generalized soft-threshold Dikin walk beyond log-barrier. We further extend our result to show how to sample from a $d$-dimensional spectrahedron, the constrained set of a semidefinite program, specified by the set $\{x\in \mathbb{R}^d: \sum_{i=1}^d x_i A_i \succeq C \}$ where $A_1,\ldots,A_d, C$ are $n\times n$ real symmetric matrices. We design a walk that mixes in $\widetilde O((nd+dL^2R^2)\log(w/\delta))$ steps with a per iteration cost of $\widetilde O(n^\omega+n^2d^{3\omega-5})$. We improve the mixing time bound of prior best Dikin walk due to Narayanan and Rakhlin that mixes in $\widetilde O((n^2d^3+n^2dL^2R^2)\log(w/\delta))$ steps.

Diff-BBO: Diffusion-Based Inverse Modeling for Black-Box Optimization

Black-box optimization (BBO) aims to optimize an objective function by iteratively querying a black-box oracle. This process demands sample-efficient optimization due to the high computational cost of function evaluations. While prior studies focus on forward approaches to learn surrogates for the unknown objective function, they struggle with high-dimensional inputs where valid inputs form a small subspace (e.g., valid protein sequences), which is common in real-world tasks. Recently, diffusion models have demonstrated impressive capability in learning the high-dimensional data manifold. They have shown promising performance in black-box optimization tasks but only in offline settings. In this work, we propose diffusion-based inverse modeling for black-box optimization (Diff-BBO), the first inverse approach leveraging diffusion models for online BBO problem. Diff-BBO distinguishes itself from forward approaches through the design of acquisition function. Instead of proposing candidates in the design space, Diff-BBO employs a novel acquisition function Uncertainty-aware Exploration (UaE) to propose objective function values, which leverages the uncertainty of a conditional diffusion model to generate samples in the design space. Theoretically, we prove that using UaE leads to optimal optimization outcomes. Empirically, we redesign experiments on the Design-Bench benchmark for online settings and show that Diff-BBO achieves state-of-the-art performance.

Demystifying SGD with Doubly Stochastic Gradients

Optimization objectives in the form of a sum of intractable expectations are rising in importance (e.g., diffusion models, variational autoencoders, and many more), a setting also known as "finite sum with infinite data." For these problems, a popular strategy is to employ SGD with doubly stochastic gradients (doubly SGD): the expectations are estimated using the gradient estimator of each component, while the sum is estimated by subsampling over these estimators. Despite its popularity, little is known about the convergence properties of doubly SGD, except under strong assumptions such as bounded variance. In this work, we establish the convergence of doubly SGD with independent minibatching and random reshuffling under general conditions, which encompasses dependent component gradient estimators. In particular, for dependent estimators, our analysis allows fined-grained analysis of the effect correlations. As a result, under a per-iteration computational budget of $b \times m$, where $b$ is the minibatch size and $m$ is the number of Monte Carlo samples, our analysis suggests where one should invest most of the budget in general. Furthermore, we prove that random reshuffling (RR) improves the complexity dependence on the subsampling noise.