Log-concave Sampling over a Convex Body with a Barrier: a Robust and Unified Dikin Walk

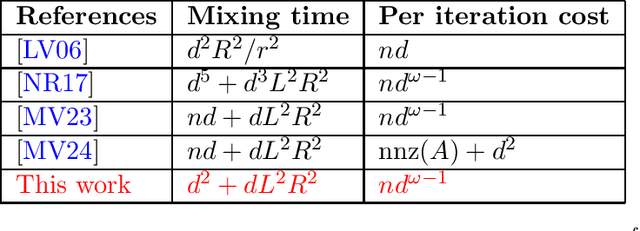
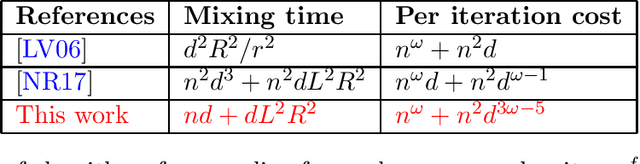
We consider the problem of sampling from a $d$-dimensional log-concave distribution $\pi(\theta) \propto \exp(-f(\theta))$ for $L$-Lipschitz $f$, constrained to a convex body with an efficiently computable self-concordant barrier function, contained in a ball of radius $R$ with a $w$-warm start. We propose a \emph{robust} sampling framework that computes spectral approximations to the Hessian of the barrier functions in each iteration. We prove that for polytopes that are described by $n$ hyperplanes, sampling with the Lee-Sidford barrier function mixes within $\widetilde O((d^2+dL^2R^2)\log(w/\delta))$ steps with a per step cost of $\widetilde O(nd^{\omega-1})$, where $\omega\approx 2.37$ is the fast matrix multiplication exponent. Compared to the prior work of Mangoubi and Vishnoi, our approach gives faster mixing time as we are able to design a generalized soft-threshold Dikin walk beyond log-barrier. We further extend our result to show how to sample from a $d$-dimensional spectrahedron, the constrained set of a semidefinite program, specified by the set $\{x\in \mathbb{R}^d: \sum_{i=1}^d x_i A_i \succeq C \}$ where $A_1,\ldots,A_d, C$ are $n\times n$ real symmetric matrices. We design a walk that mixes in $\widetilde O((nd+dL^2R^2)\log(w/\delta))$ steps with a per iteration cost of $\widetilde O(n^\omega+n^2d^{3\omega-5})$. We improve the mixing time bound of prior best Dikin walk due to Narayanan and Rakhlin that mixes in $\widetilde O((n^2d^3+n^2dL^2R^2)\log(w/\delta))$ steps.

Binary Hypothesis Testing for Softmax Models and Leverage Score Models

Softmax distributions are widely used in machine learning, including Large Language Models (LLMs) where the attention unit uses softmax distributions. We abstract the attention unit as the softmax model, where given a vector input, the model produces an output drawn from the softmax distribution (which depends on the vector input). We consider the fundamental problem of binary hypothesis testing in the setting of softmax models. That is, given an unknown softmax model, which is known to be one of the two given softmax models, how many queries are needed to determine which one is the truth? We show that the sample complexity is asymptotically $O(\epsilon^{-2})$ where $\epsilon$ is a certain distance between the parameters of the models. Furthermore, we draw analogy between the softmax model and the leverage score model, an important tool for algorithm design in linear algebra and graph theory. The leverage score model, on a high level, is a model which, given vector input, produces an output drawn from a distribution dependent on the input. We obtain similar results for the binary hypothesis testing problem for leverage score models.

Generalized Rainbow Differential Privacy

We study a new framework for designing differentially private (DP) mechanisms via randomized graph colorings, called rainbow differential privacy. In this framework, datasets are nodes in a graph, and two neighboring datasets are connected by an edge. Each dataset in the graph has a preferential ordering for the possible outputs of the mechanism, and these orderings are called rainbows. Different rainbows partition the graph of connected datasets into different regions. We show that if a DP mechanism at the boundary of such regions is fixed and it behaves identically for all same-rainbow boundary datasets, then a unique optimal $(\epsilon,\delta)$-DP mechanism exists (as long as the boundary condition is valid) and can be expressed in closed-form. Our proof technique is based on an interesting relationship between dominance ordering and DP, which applies to any finite number of colors and for $(\epsilon,\delta)$-DP, improving upon previous results that only apply to at most three colors and for $\epsilon$-DP. We justify the homogeneous boundary condition assumption by giving an example with non-homogeneous boundary condition, for which there exists no optimal DP mechanism.

A Nearly-Linear Time Algorithm for Structured Support Vector Machines

Quadratic programming is a fundamental problem in the field of convex optimization. Many practical tasks can be formulated as quadratic programming, for example, the support vector machine (SVM). Linear SVM is one of the most popular tools over the last three decades in machine learning before deep learning method dominating. In general, a quadratic program has input size $\Theta(n^2)$ (where $n$ is the number of variables), thus takes $\Omega(n^2)$ time to solve. Nevertheless, quadratic programs coming from SVMs has input size $O(n)$, allowing the possibility of designing nearly-linear time algorithms. Two important classes of SVMs are programs admitting low-rank kernel factorizations and low-treewidth programs. Low-treewidth convex optimization has gained increasing interest in the past few years (e.g.~linear programming [Dong, Lee and Ye 2021] and semidefinite programming [Gu and Song 2022]). Therefore, an important open question is whether there exist nearly-linear time algorithms for quadratic programs with these nice structures. In this work, we provide the first nearly-linear time algorithm for solving quadratic programming with low-rank factorization or low-treewidth, and a small number of linear constraints. Our results imply nearly-linear time algorithms for low-treewidth or low-rank SVMs.

Low Rank Matrix Completion via Robust Alternating Minimization in Nearly Linear Time

Given a matrix $M\in \mathbb{R}^{m\times n}$, the low rank matrix completion problem asks us to find a rank-$k$ approximation of $M$ as $UV^\top$ for $U\in \mathbb{R}^{m\times k}$ and $V\in \mathbb{R}^{n\times k}$ by only observing a few entries masked by a binary matrix $P_{\Omega}\in \{0, 1 \}^{m\times n}$. As a particular instance of the weighted low rank approximation problem, solving low rank matrix completion is known to be computationally hard even to find an approximate solution [RSW16]. However, due to its practical importance, many heuristics have been proposed for this problem. In the seminal work of Jain, Netrapalli, and Sanghavi [JNS13], they show that the alternating minimization framework provides provable guarantees for low rank matrix completion problem whenever $M$ admits an incoherent low rank factorization. Unfortunately, their algorithm requires solving two exact multiple response regressions per iteration and their analysis is non-robust as they exploit the structure of the exact solution. In this paper, we take a major step towards a more efficient and robust alternating minimization framework for low rank matrix completion. Our main result is a robust alternating minimization algorithm that can tolerate moderate errors even though the regressions are solved approximately. Consequently, we also significantly improve the running time of [JNS13] from $\widetilde{O}(mnk^2 )$ to $\widetilde{O}(mnk )$ which is nearly linear in the problem size, as verifying the low rank approximation takes $O(mnk)$ time. Our core algorithmic building block is a high accuracy regression solver that solves the regression in nearly linear time per iteration.