Comparing privacy notions for protection against reconstruction attacks in machine learning

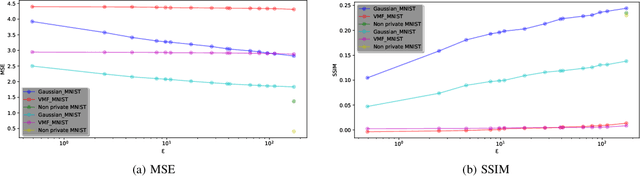
Within the machine learning community, reconstruction attacks are a principal concern and have been identified even in federated learning (FL), which was designed with privacy preservation in mind. In response to these threats, the privacy community recommends the use of differential privacy (DP) in the stochastic gradient descent algorithm, termed DP-SGD. However, the proliferation of variants of DP in recent years\textemdash such as metric privacy\textemdash has made it challenging to conduct a fair comparison between different mechanisms due to the different meanings of the privacy parameters $\epsilon$ and $\delta$ across different variants. Thus, interpreting the practical implications of $\epsilon$ and $\delta$ in the FL context and amongst variants of DP remains ambiguous. In this paper, we lay a foundational framework for comparing mechanisms with differing notions of privacy guarantees, namely $(\epsilon,\delta)$-DP and metric privacy. We provide two foundational means of comparison: firstly, via the well-established $(\epsilon,\delta)$-DP guarantees, made possible through the R\'enyi differential privacy framework; and secondly, via Bayes' capacity, which we identify as an appropriate measure for reconstruction threats.

Bayes' capacity as a measure for reconstruction attacks in federated learning

Within the machine learning community, reconstruction attacks are a principal attack of concern and have been identified even in federated learning, which was designed with privacy preservation in mind. In federated learning, it has been shown that an adversary with knowledge of the machine learning architecture is able to infer the exact value of a training element given an observation of the weight updates performed during stochastic gradient descent. In response to these threats, the privacy community recommends the use of differential privacy in the stochastic gradient descent algorithm, termed DP-SGD. However, DP has not yet been formally established as an effective countermeasure against reconstruction attacks. In this paper, we formalise the reconstruction threat model using the information-theoretic framework of quantitative information flow. We show that the Bayes' capacity, related to the Sibson mutual information of order infinity, represents a tight upper bound on the leakage of the DP-SGD algorithm to an adversary interested in performing a reconstruction attack. We provide empirical results demonstrating the effectiveness of this measure for comparing mechanisms against reconstruction threats.

Generalized Rainbow Differential Privacy

We study a new framework for designing differentially private (DP) mechanisms via randomized graph colorings, called rainbow differential privacy. In this framework, datasets are nodes in a graph, and two neighboring datasets are connected by an edge. Each dataset in the graph has a preferential ordering for the possible outputs of the mechanism, and these orderings are called rainbows. Different rainbows partition the graph of connected datasets into different regions. We show that if a DP mechanism at the boundary of such regions is fixed and it behaves identically for all same-rainbow boundary datasets, then a unique optimal $(\epsilon,\delta)$-DP mechanism exists (as long as the boundary condition is valid) and can be expressed in closed-form. Our proof technique is based on an interesting relationship between dominance ordering and DP, which applies to any finite number of colors and for $(\epsilon,\delta)$-DP, improving upon previous results that only apply to at most three colors and for $\epsilon$-DP. We justify the homogeneous boundary condition assumption by giving an example with non-homogeneous boundary condition, for which there exists no optimal DP mechanism.

Age of Information in Downlink Systems: Broadcast or Distributed Transmission?

We analytically decide whether the broadcast transmission scheme or the distributed transmission scheme achieves the optimal age of information (AoI) performance of a multiuser system where a base station (BS) generates and transmits status updates to multiple user equipments (UEs). In the broadcast transmission scheme, the status update for all UEs is jointly encoded into a packet for transmission, while in the distributed transmission scheme, the status update for each UE is encoded individually and transmitted by following the round robin policy. For both transmission schemes, we examine three packet management strategies, namely the non-preemption strategy, the preemption in buffer strategy, and the preemption in serving strategy. We first derive new closed-form expressions for the average AoI achieved by two transmission schemes with three packet management strategies. Based on them, we compare the AoI performance of two transmission schemes in two systems, namely, the remote control system and the dynamic system. Aided by simulation results, we verify our analysis and investigate the impact of system parameters on the average AoI. For example, the distributed transmission scheme is more appropriate for the system with a large number UEs. Otherwise, the broadcast transmission scheme is more appropriate.

Rainbow Differential Privacy

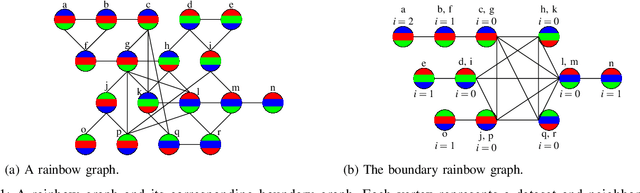
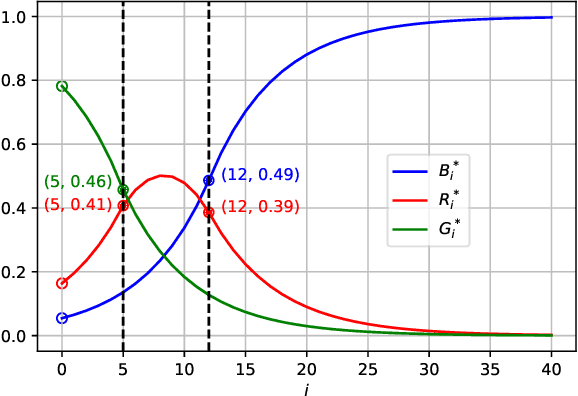
We extend a previous framework for designing differentially private (DP) mechanisms via randomized graph colorings that was restricted to binary functions, corresponding to colorings in a graph, to multi-valued functions. As before, datasets are nodes in the graph and any two neighboring datasets are connected by an edge. In our setting, we assume each dataset has a preferential ordering for the possible outputs of the mechanism, which we refer to as a rainbow. Different rainbows partition the graph of datasets into different regions. We show that when the DP mechanism is pre-specified at the boundary of such regions, at most one optimal mechanism can exist. Moreover, if the mechanism is to behave identically for all same-rainbow boundary datasets, the problem can be greatly simplified and solved by means of a morphism to a line graph. We then show closed form expressions for the line graph in the case of ternary functions. Treatment of ternary queries in this paper displays enough richness to be extended to higher-dimensional query spaces with preferential query ordering, but the optimality proof does not seem to follow directly from the ternary proof.

The Age of Information of Short-Packet Communications: Joint or Distributed Encoding?

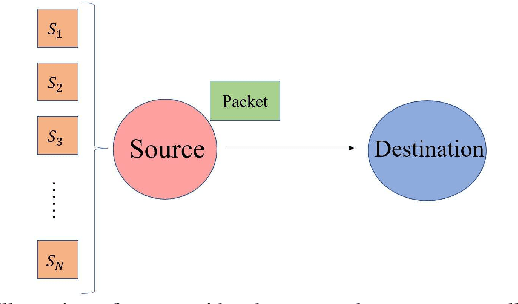
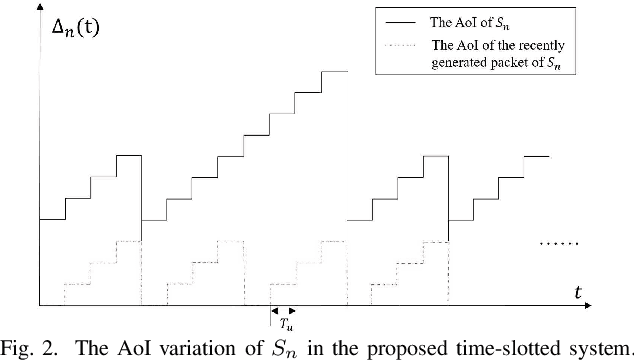
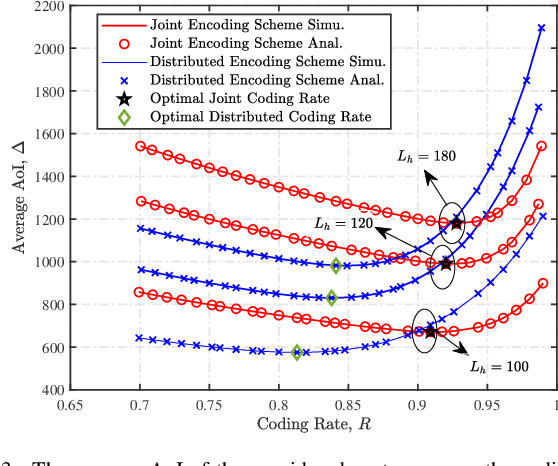
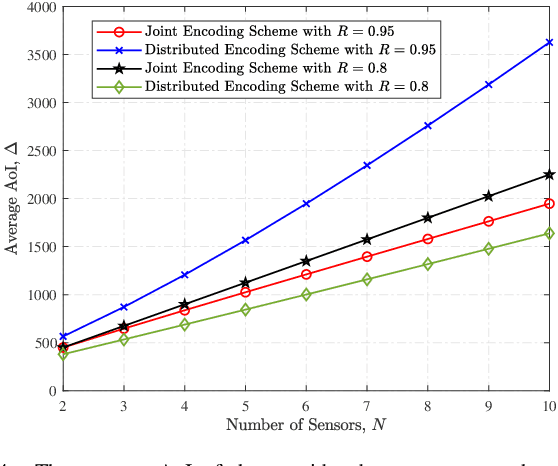
In this paper, we analyze the impact of different encoding schemes on the age of information (AoI) performance in a point-to-point system, where a source generates packets based on the status updates collected from multiple sensors and transmits the packets to a destination. In this system, we consider two encoding schemes, namely, the joint encoding scheme and the distributed encoding scheme. In the joint encoding scheme, the status updates from all the sensors are jointly encoded into a packet for transmission. In the distributed encoding scheme, the status update from each sensor is encoded individually and the sensors' packets are transmitted following the round robin policy. To ensure the freshness of packets, the zero-wait policy is adopted in both schemes, where a new packet is immediately generated once the source finishes the transmission of the current packet. We derive closed-form expressions for the average AoI achieved by these two encoding schemes and compare their performances. Simulation results show that the distributed encoding scheme is more appropriate for systems with a relatively large number of sensors, compared with the joint encoding scheme.

On Monotonicity of the Optimal Transmission Policy in Cross-layer Adaptive m-QAM Modulation

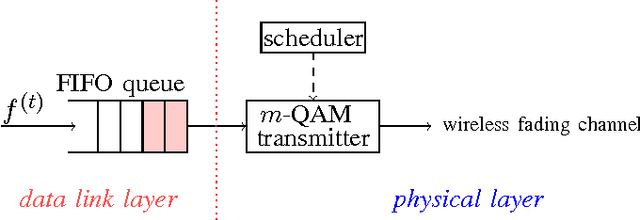
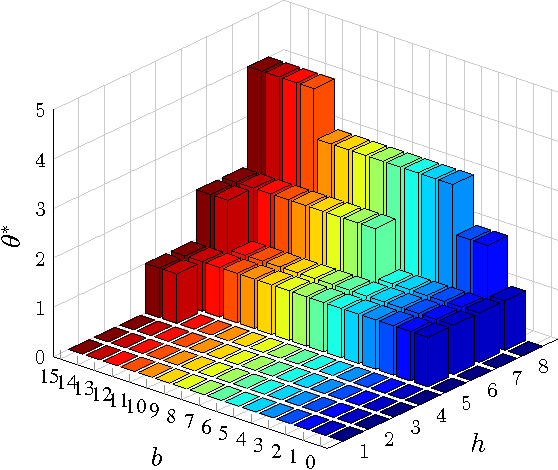
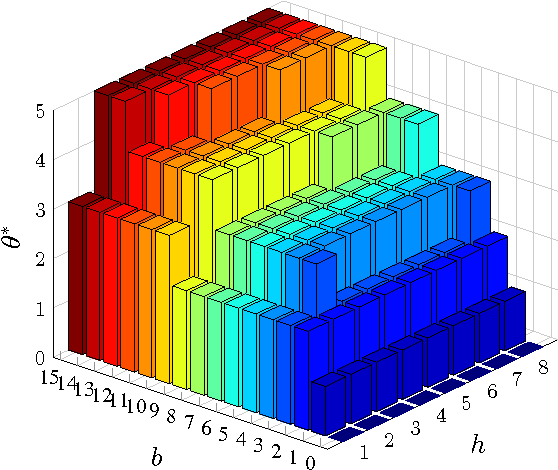
This paper considers a cross-layer adaptive modulation system that is modeled as a Markov decision process (MDP). We study how to utilize the monotonicity of the optimal transmission policy to relieve the computational complexity of dynamic programming (DP). In this system, a scheduler controls the bit rate of the m-quadrature amplitude modulation (m-QAM) in order to minimize the long-term losses incurred by the queue overflow in the data link layer and the transmission power consumption in the physical layer. The work is done in two steps. Firstly, we observe the L-natural-convexity and submodularity of DP to prove that the optimal policy is always nondecreasing in queue occupancy/state and derive the sufficient condition for it to be nondecreasing in both queue and channel states. We also show that, due to the L-natural-convexity of DP, the variation of the optimal policy in queue state is restricted by a bounded marginal effect: The increment of the optimal policy between adjacent queue states is no greater than one. Secondly, we use the monotonicity results to present two low complexity algorithms: monotonic policy iteration (MPI) based on L-natural-convexity and discrete simultaneous perturbation stochastic approximation (DSPSA). We run experiments to show that the time complexity of MPI based on L-natural-convexity is much lower than that of DP and the conventional MPI that is based on submodularity and DSPSA is able to adaptively track the optimal policy when the system parameters change.

Structured Optimal Transmission Control in Network-coded Two-way Relay Channels

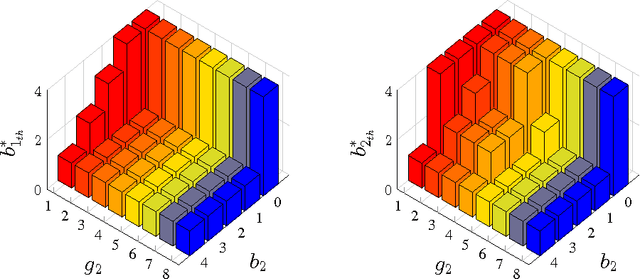
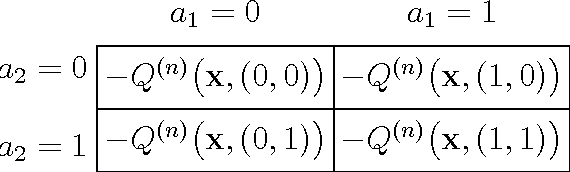
This paper considers a transmission control problem in network-coded two-way relay channels (NC-TWRC), where the relay buffers random symbol arrivals from two users, and the channels are assumed to be fading. The problem is modeled by a discounted infinite horizon Markov decision process (MDP). The objective is to find a transmission control policy that minimizes the symbol delay, buffer overflow and transmission power consumption and error rate simultaneously and in the long run. By using the concepts of submodularity, multimodularity and L-natural convexity, we study the structure of the optimal policy searched by dynamic programming (DP) algorithm. We show that the optimal transmission policy is nondecreasing in queue occupancies or/and channel states under certain conditions such as the chosen values of parameters in the MDP model, channel modeling method, modulation scheme and the preservation of stochastic dominance in the transitions of system states. The results derived in this paper can be used to relieve the high complexity of DP and facilitate real-time control.