Rainbow Differential Privacy

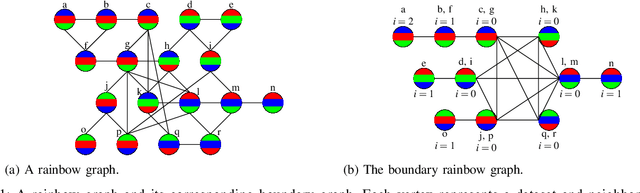
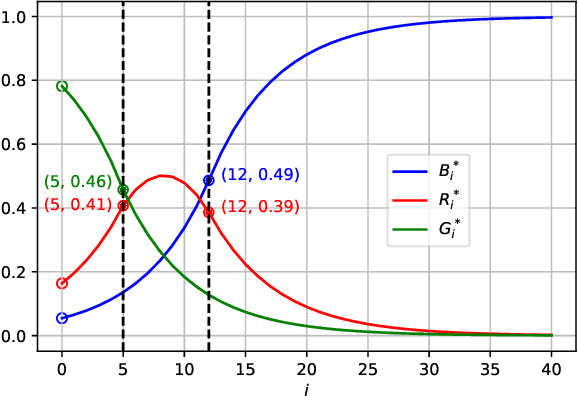
We extend a previous framework for designing differentially private (DP) mechanisms via randomized graph colorings that was restricted to binary functions, corresponding to colorings in a graph, to multi-valued functions. As before, datasets are nodes in the graph and any two neighboring datasets are connected by an edge. In our setting, we assume each dataset has a preferential ordering for the possible outputs of the mechanism, which we refer to as a rainbow. Different rainbows partition the graph of datasets into different regions. We show that when the DP mechanism is pre-specified at the boundary of such regions, at most one optimal mechanism can exist. Moreover, if the mechanism is to behave identically for all same-rainbow boundary datasets, the problem can be greatly simplified and solved by means of a morphism to a line graph. We then show closed form expressions for the line graph in the case of ternary functions. Treatment of ternary queries in this paper displays enough richness to be extended to higher-dimensional query spaces with preferential query ordering, but the optimality proof does not seem to follow directly from the ternary proof.