Structured Optimal Transmission Control in Network-coded Two-way Relay Channels
Paper and Code
Oct 29, 2013
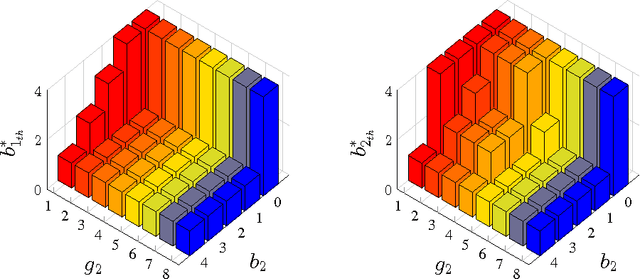

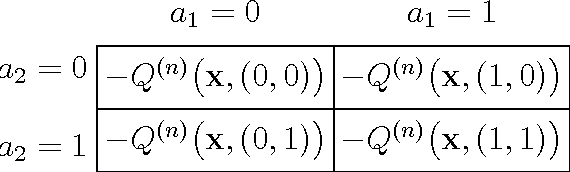
This paper considers a transmission control problem in network-coded two-way relay channels (NC-TWRC), where the relay buffers random symbol arrivals from two users, and the channels are assumed to be fading. The problem is modeled by a discounted infinite horizon Markov decision process (MDP). The objective is to find a transmission control policy that minimizes the symbol delay, buffer overflow and transmission power consumption and error rate simultaneously and in the long run. By using the concepts of submodularity, multimodularity and L-natural convexity, we study the structure of the optimal policy searched by dynamic programming (DP) algorithm. We show that the optimal transmission policy is nondecreasing in queue occupancies or/and channel states under certain conditions such as the chosen values of parameters in the MDP model, channel modeling method, modulation scheme and the preservation of stochastic dominance in the transitions of system states. The results derived in this paper can be used to relieve the high complexity of DP and facilitate real-time control.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge