An Optimal Dimensionality Multi-shell Sampling Scheme with Accurate and Efficient Transforms for Diffusion MRI

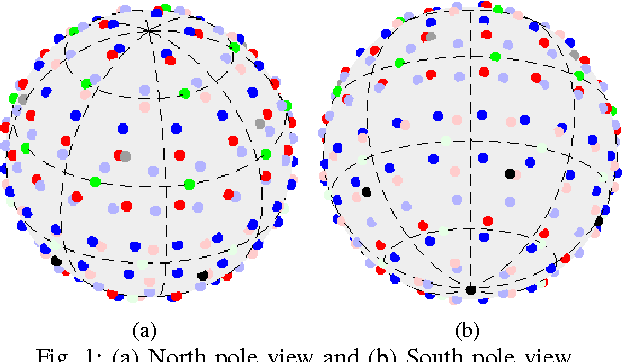
This paper proposes a multi-shell sampling scheme and corresponding transforms for the accurate reconstruction of the diffusion signal in diffusion MRI by expansion in the spherical polar Fourier (SPF) basis. The sampling scheme uses an optimal number of samples, equal to the degrees of freedom of the band-limited diffusion signal in the SPF domain, and allows for computationally efficient reconstruction. We use synthetic data sets to demonstrate that the proposed scheme allows for greater reconstruction accuracy of the diffusion signal than the multi-shell sampling schemes obtained using the generalised electrostatic energy minimisation (gEEM) method used in the Human Connectome Project. We also demonstrate that the proposed sampling scheme allows for increased angular discrimination and improved rotational invariance of reconstruction accuracy than the gEEM schemes.

On Monotonicity of the Optimal Transmission Policy in Cross-layer Adaptive m-QAM Modulation

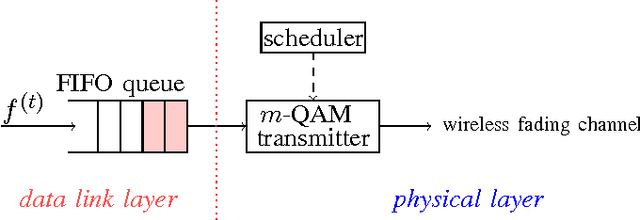
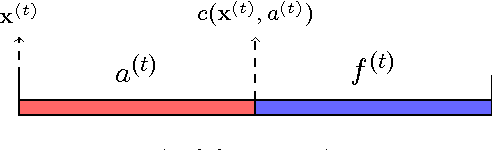
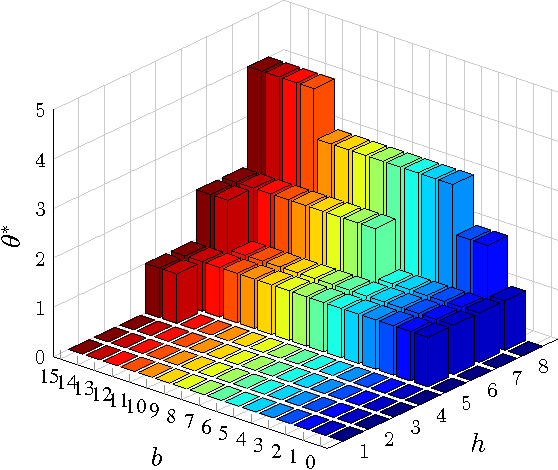
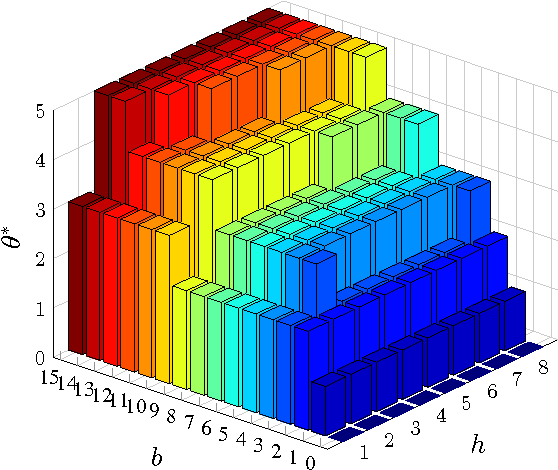
This paper considers a cross-layer adaptive modulation system that is modeled as a Markov decision process (MDP). We study how to utilize the monotonicity of the optimal transmission policy to relieve the computational complexity of dynamic programming (DP). In this system, a scheduler controls the bit rate of the m-quadrature amplitude modulation (m-QAM) in order to minimize the long-term losses incurred by the queue overflow in the data link layer and the transmission power consumption in the physical layer. The work is done in two steps. Firstly, we observe the L-natural-convexity and submodularity of DP to prove that the optimal policy is always nondecreasing in queue occupancy/state and derive the sufficient condition for it to be nondecreasing in both queue and channel states. We also show that, due to the L-natural-convexity of DP, the variation of the optimal policy in queue state is restricted by a bounded marginal effect: The increment of the optimal policy between adjacent queue states is no greater than one. Secondly, we use the monotonicity results to present two low complexity algorithms: monotonic policy iteration (MPI) based on L-natural-convexity and discrete simultaneous perturbation stochastic approximation (DSPSA). We run experiments to show that the time complexity of MPI based on L-natural-convexity is much lower than that of DP and the conventional MPI that is based on submodularity and DSPSA is able to adaptively track the optimal policy when the system parameters change.

Structured Optimal Transmission Control in Network-coded Two-way Relay Channels

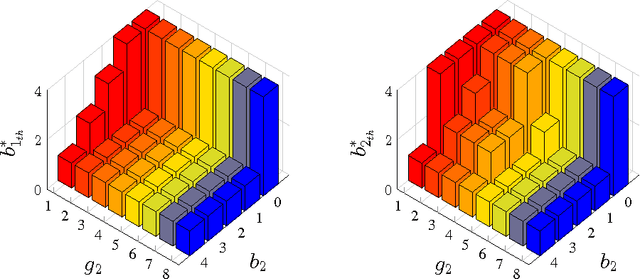
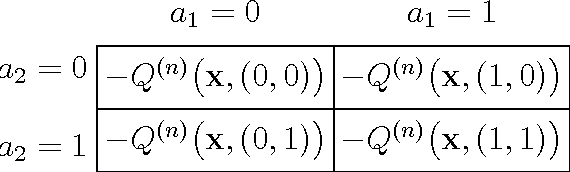
This paper considers a transmission control problem in network-coded two-way relay channels (NC-TWRC), where the relay buffers random symbol arrivals from two users, and the channels are assumed to be fading. The problem is modeled by a discounted infinite horizon Markov decision process (MDP). The objective is to find a transmission control policy that minimizes the symbol delay, buffer overflow and transmission power consumption and error rate simultaneously and in the long run. By using the concepts of submodularity, multimodularity and L-natural convexity, we study the structure of the optimal policy searched by dynamic programming (DP) algorithm. We show that the optimal transmission policy is nondecreasing in queue occupancies or/and channel states under certain conditions such as the chosen values of parameters in the MDP model, channel modeling method, modulation scheme and the preservation of stochastic dominance in the transitions of system states. The results derived in this paper can be used to relieve the high complexity of DP and facilitate real-time control.