LoFi: Scalable Local Image Reconstruction with Implicit Neural Representation

Neural fields or implicit neural representations (INRs) have attracted significant attention in machine learning and signal processing due to their efficient continuous representation of images and 3D volumes. In this work, we build on INRs and introduce a coordinate-based local processing framework for solving imaging inverse problems, termed LoFi (Local Field). Unlike conventional methods for image reconstruction, LoFi processes local information at each coordinate \textit{separately} by multi-layer perceptrons (MLPs), recovering the object at that specific coordinate. Similar to INRs, LoFi can recover images at any continuous coordinate, enabling image reconstruction at multiple resolutions. With comparable or better performance than standard CNNs for image reconstruction, LoFi achieves excellent generalization to out-of-distribution data and memory usage almost independent of image resolution. Remarkably, training on $1024 \times 1024$ images requires just 3GB of memory -- over 20 times less than the memory typically needed by standard CNNs. Additionally, LoFi's local design allows it to train on extremely small datasets with less than 10 samples, without overfitting or the need for regularization or early stopping. Finally, we use LoFi as a denoising prior in a plug-and-play framework for solving general inverse problems to benefit from its continuous image representation and strong generalization. Although trained on low-resolution images, LoFi can be used as a low-dimensional prior to solve inverse problems at any resolution. We validate our framework across a variety of imaging modalities, from low-dose computed tomography to radio interferometric imaging.

Accelerated Bayesian parameter estimation and model selection for gravitational waves with normalizing flows

We present an accelerated pipeline, based on high-performance computing techniques and normalizing flows, for joint Bayesian parameter estimation and model selection and demonstrate its efficiency in gravitational wave astrophysics. We integrate the Jim inference toolkit, a normalizing flow-enhanced Markov chain Monte Carlo (MCMC) sampler, with the learned harmonic mean estimator. Our Bayesian evidence estimates run on $1$ GPU are consistent with traditional nested sampling techniques run on $16$ CPU cores, while reducing the computation time by factors of $5\times$ and $15\times$ for $4$-dimensional and $11$-dimensional gravitational wave inference problems, respectively. Our code is available in well-tested and thoroughly documented open-source packages, ensuring accessibility and reproducibility for the wider research community.

Simulation-based inference with scattering representations: scattering is all you need

We demonstrate the first successful use of scattering representations without further compression for simulation-based inference (SBI) with images (i.e. field-level), illustrated with a cosmological case study. Scattering representations provide a highly effective representational space for subsequent learning tasks, although the higher dimensional compressed space introduces challenges. We overcome these through spatial averaging, coupled with more expressive density estimators. Compared to alternative methods, such an approach does not require additional simulations for either training or computing derivatives, is interpretable, and resilient to covariate shift. As expected, we show that a scattering only approach extracts more information than traditional second order summary statistics.

The future of cosmological likelihood-based inference: accelerated high-dimensional parameter estimation and model comparison

We advocate for a new paradigm of cosmological likelihood-based inference, leveraging recent developments in machine learning and its underlying technology, to accelerate Bayesian inference in high-dimensional settings. Specifically, we combine (i) emulation, where a machine learning model is trained to mimic cosmological observables, e.g. CosmoPower-JAX; (ii) differentiable and probabilistic programming, e.g. JAX and NumPyro, respectively; (iii) scalable Markov chain Monte Carlo (MCMC) sampling techniques that exploit gradients, e.g. Hamiltonian Monte Carlo; and (iv) decoupled and scalable Bayesian model selection techniques that compute the Bayesian evidence purely from posterior samples, e.g. the learned harmonic mean implemented in harmonic. This paradigm allows us to carry out a complete Bayesian analysis, including both parameter estimation and model selection, in a fraction of the time of traditional approaches. First, we demonstrate the application of this paradigm on a simulated cosmic shear analysis for a Stage IV survey in 37- and 39-dimensional parameter spaces, comparing $\Lambda$CDM and a dynamical dark energy model ($w_0w_a$CDM). We recover posterior contours and evidence estimates that are in excellent agreement with those computed by the traditional nested sampling approach while reducing the computational cost from 8 months on 48 CPU cores to 2 days on 12 GPUs. Second, we consider a joint analysis between three simulated next-generation surveys, each performing a 3x2pt analysis, resulting in 157- and 159-dimensional parameter spaces. Standard nested sampling techniques are simply not feasible in this high-dimensional setting, requiring a projected 12 years of compute time on 48 CPU cores; on the other hand, the proposed approach only requires 8 days of compute time on 24 GPUs. All packages used in our analyses are publicly available.

Learned radio interferometric imaging for varying visibility coverage

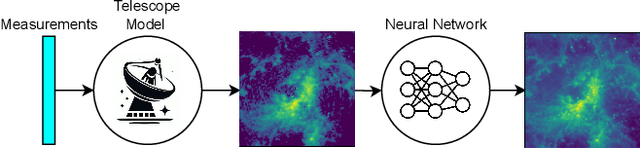
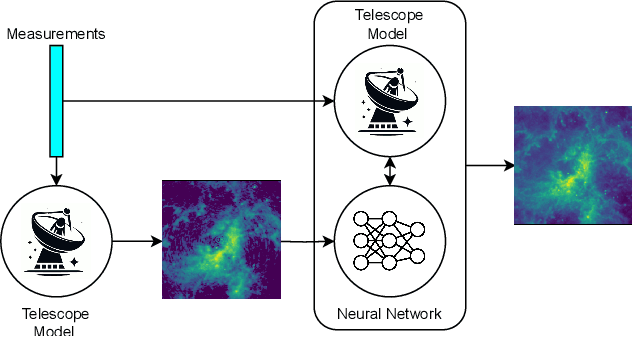
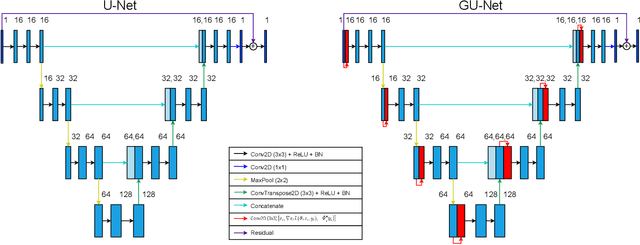
With the next generation of interferometric telescopes, such as the Square Kilometre Array (SKA), the need for highly computationally efficient reconstruction techniques is particularly acute. The challenge in designing learned, data-driven reconstruction techniques for radio interferometry is that they need to be agnostic to the varying visibility coverages of the telescope, since these are different for each observation. Because of this, learned post-processing or learned unrolled iterative reconstruction methods must typically be retrained for each specific observation, amounting to a large computational overhead. In this work we develop learned post-processing and unrolled iterative methods for varying visibility coverages, proposing training strategies to make these methods agnostic to variations in visibility coverage with minimal to no fine-tuning. Learned post-processing techniques are heavily dependent on the prior information encoded in training data and generalise poorly to other visibility coverages. In contrast, unrolled iterative methods, which include the telescope measurement operator inside the network, achieve state-of-the-art reconstruction quality and computation time, generalising well to other coverages and require little to no fine-tuning. Furthermore, they generalise well to realistic radio observations and are able to reconstruct the high dynamic range of these images.

Differentiable and accelerated wavelet transforms on the sphere and ball

Directional wavelet dictionaries are hierarchical representations which efficiently capture and segment information across scale, location and orientation. Such representations demonstrate a particular affinity to physical signals, which often exhibit highly anisotropic, localised multiscale structure. Many physically important signals are observed over spherical domains, such as the celestial sky in cosmology. Leveraging recent advances in computational harmonic analysis, we design new highly distributable and automatically differentiable directional wavelet transforms on the $2$-dimensional sphere $\mathbb{S}^2$ and $3$-dimensional ball $\mathbb{B}^3 = \mathbb{R}^+ \times \mathbb{S}^2$ (the space formed by augmenting the sphere with the radial half-line). We observe up to a $300$-fold and $21800$-fold acceleration for signals on the sphere and ball, respectively, compared to existing software, whilst maintaining 64-bit machine precision. Not only do these algorithms dramatically accelerate existing spherical wavelet transforms, the gradient information afforded by automatic differentiation unlocks many data-driven analysis techniques previously not possible for these spaces. We publicly release both S2WAV and S2BALL, open-sourced JAX libraries for our transforms that are automatically differentiable and readily deployable both on and over clusters of hardware accelerators (e.g. GPUs & TPUs).

Scalable Bayesian uncertainty quantification with data-driven priors for radio interferometric imaging

Next-generation radio interferometers like the Square Kilometer Array have the potential to unlock scientific discoveries thanks to their unprecedented angular resolution and sensitivity. One key to unlocking their potential resides in handling the deluge and complexity of incoming data. This challenge requires building radio interferometric imaging methods that can cope with the massive data sizes and provide high-quality image reconstructions with uncertainty quantification (UQ). This work proposes a method coined QuantifAI to address UQ in radio-interferometric imaging with data-driven (learned) priors for high-dimensional settings. Our model, rooted in the Bayesian framework, uses a physically motivated model for the likelihood. The model exploits a data-driven convex prior, which can encode complex information learned implicitly from simulations and guarantee the log-concavity of the posterior. We leverage probability concentration phenomena of high-dimensional log-concave posteriors that let us obtain information about the posterior, avoiding MCMC sampling techniques. We rely on convex optimisation methods to compute the MAP estimation, which is known to be faster and better scale with dimension than MCMC sampling strategies. Our method allows us to compute local credible intervals, i.e., Bayesian error bars, and perform hypothesis testing of structure on the reconstructed image. In addition, we propose a novel blazing-fast method to compute pixel-wise uncertainties at different scales. We demonstrate our method by reconstructing radio-interferometric images in a simulated setting and carrying out fast and scalable UQ, which we validate with MCMC sampling. Our method shows an improved image quality and more meaningful uncertainties than the benchmark method based on a sparsity-promoting prior. QuantifAI's source code: https://github.com/astro-informatics/QuantifAI.

Differentiable and accelerated spherical harmonic and Wigner transforms

Many areas of science and engineering encounter data defined on spherical manifolds. Modelling and analysis of spherical data often necessitates spherical harmonic transforms, at high degrees, and increasingly requires efficient computation of gradients for machine learning or other differentiable programming tasks. We develop novel algorithmic structures for accelerated and differentiable computation of generalised Fourier transforms on the sphere $\mathbb{S}^2$ and rotation group $\text{SO}(3)$, i.e. spherical harmonic and Wigner transforms, respectively. We present a recursive algorithm for the calculation of Wigner $d$-functions that is both stable to high harmonic degrees and extremely parallelisable. By tightly coupling this with separable spherical transforms, we obtain algorithms that exhibit an extremely parallelisable structure that is well-suited for the high throughput computing of modern hardware accelerators (e.g. GPUs). We also develop a hybrid automatic and manual differentiation approach so that gradients can be computed efficiently. Our algorithms are implemented within the JAX differentiable programming framework in the S2FFT software code. Numerous samplings of the sphere are supported, including equiangular and HEALPix sampling. Computational errors are at the order of machine precision for spherical samplings that admit a sampling theorem. When benchmarked against alternative C codes we observe up to a 400-fold acceleration. Furthermore, when distributing over multiple GPUs we achieve very close to optimal linear scaling with increasing number of GPUs due to the highly parallelised and balanced nature of our algorithms. Provided access to sufficiently many GPUs our transforms thus exhibit an unprecedented effective linear time complexity.

Learned harmonic mean estimation of the marginal likelihood with normalizing flows

Computing the marginal likelihood (also called the Bayesian model evidence) is an important task in Bayesian model selection, providing a principled quantitative way to compare models. The learned harmonic mean estimator solves the exploding variance problem of the original harmonic mean estimation of the marginal likelihood. The learned harmonic mean estimator learns an importance sampling target distribution that approximates the optimal distribution. While the approximation need not be highly accurate, it is critical that the probability mass of the learned distribution is contained within the posterior in order to avoid the exploding variance problem. In previous work a bespoke optimization problem is introduced when training models in order to ensure this property is satisfied. In the current article we introduce the use of normalizing flows to represent the importance sampling target distribution. A flow-based model is trained on samples from the posterior by maximum likelihood estimation. Then, the probability density of the flow is concentrated by lowering the variance of the base distribution, i.e. by lowering its "temperature", ensuring its probability mass is contained within the posterior. This approach avoids the need for a bespoke optimisation problem and careful fine tuning of parameters, resulting in a more robust method. Moreover, the use of normalizing flows has the potential to scale to high dimensional settings. We present preliminary experiments demonstrating the effectiveness of the use of flows for the learned harmonic mean estimator. The harmonic code implementing the learned harmonic mean, which is publicly available, has been updated to now support normalizing flows.

Proximal nested sampling with data-driven priors for physical scientists

Proximal nested sampling was introduced recently to open up Bayesian model selection for high-dimensional problems such as computational imaging. The framework is suitable for models with a log-convex likelihood, which are ubiquitous in the imaging sciences. The purpose of this article is two-fold. First, we review proximal nested sampling in a pedagogical manner in an attempt to elucidate the framework for physical scientists. Second, we show how proximal nested sampling can be extended in an empirical Bayes setting to support data-driven priors, such as deep neural networks learned from training data.