LoFi: Scalable Local Image Reconstruction with Implicit Neural Representation

Neural fields or implicit neural representations (INRs) have attracted significant attention in machine learning and signal processing due to their efficient continuous representation of images and 3D volumes. In this work, we build on INRs and introduce a coordinate-based local processing framework for solving imaging inverse problems, termed LoFi (Local Field). Unlike conventional methods for image reconstruction, LoFi processes local information at each coordinate \textit{separately} by multi-layer perceptrons (MLPs), recovering the object at that specific coordinate. Similar to INRs, LoFi can recover images at any continuous coordinate, enabling image reconstruction at multiple resolutions. With comparable or better performance than standard CNNs for image reconstruction, LoFi achieves excellent generalization to out-of-distribution data and memory usage almost independent of image resolution. Remarkably, training on $1024 \times 1024$ images requires just 3GB of memory -- over 20 times less than the memory typically needed by standard CNNs. Additionally, LoFi's local design allows it to train on extremely small datasets with less than 10 samples, without overfitting or the need for regularization or early stopping. Finally, we use LoFi as a denoising prior in a plug-and-play framework for solving general inverse problems to benefit from its continuous image representation and strong generalization. Although trained on low-resolution images, LoFi can be used as a low-dimensional prior to solve inverse problems at any resolution. We validate our framework across a variety of imaging modalities, from low-dose computed tomography to radio interferometric imaging.

GLIMPSE: Generalized Local Imaging with MLPs

Deep learning is the current de facto state of the art in tomographic imaging. A common approach is to feed the result of a simple inversion, for example the backprojection, to a convolutional neural network (CNN) which then computes the reconstruction. Despite strong results on 'in-distribution' test data similar to the training data, backprojection from sparse-view data delocalizes singularities, so these approaches require a large receptive field to perform well. As a consequence, they overfit to certain global structures which leads to poor generalization on out-of-distribution (OOD) samples. Moreover, their memory complexity and training time scale unfavorably with image resolution, making them impractical for application at realistic clinical resolutions, especially in 3D: a standard U-Net requires a substantial 140GB of memory and 2600 seconds per epoch on a research-grade GPU when training on 1024x1024 images. In this paper, we introduce GLIMPSE, a local processing neural network for computed tomography which reconstructs a pixel value by feeding only the measurements associated with the neighborhood of the pixel to a simple MLP. While achieving comparable or better performance with successful CNNs like the U-Net on in-distribution test data, GLIMPSE significantly outperforms them on OOD samples while maintaining a memory footprint almost independent of image resolution; 5GB memory suffices to train on 1024x1024 images. Further, we built GLIMPSE to be fully differentiable, which enables feats such as recovery of accurate projection angles if they are out of calibration.

Deep Injective Prior for Inverse Scattering

In electromagnetic inverse scattering, we aim to reconstruct object permittivity from scattered waves. Deep learning is a promising alternative to traditional iterative solvers, but it has been used mostly in a supervised framework to regress the permittivity patterns from scattered fields or back-projections. While such methods are fast at test-time and achieve good results for specific data distributions, they are sensitive to the distribution drift of the scattered fields, common in practice. If the distribution of the scattered fields changes due to changes in frequency, the number of transmitters and receivers, or any other real-world factor, an end-to-end neural network must be re-trained or fine-tuned on a new dataset. In this paper, we propose a new data-driven framework for inverse scattering based on deep generative models. We model the target permittivities by a low-dimensional manifold which acts as a regularizer and learned from data. Unlike supervised methods which require both scattered fields and target signals, we only need the target permittivities for training; it can then be used with any experimental setup. We show that the proposed framework significantly outperforms the traditional iterative methods especially for strong scatterers while having comparable reconstruction quality to state-of-the-art deep learning methods like U-Net.

FunkNN: Neural Interpolation for Functional Generation

Can we build continuous generative models which generalize across scales, can be evaluated at any coordinate, admit calculation of exact derivatives, and are conceptually simple? Existing MLP-based architectures generate worse samples than the grid-based generators with favorable convolutional inductive biases. Models that focus on generating images at different scales do better, but employ complex architectures not designed for continuous evaluation of images and derivatives. We take a signal-processing perspective and treat continuous image generation as interpolation from samples. Indeed, correctly sampled discrete images contain all information about the low spatial frequencies. The question is then how to extrapolate the spectrum in a data-driven way while meeting the above design criteria. Our answer is FunkNN -- a new convolutional network which learns how to reconstruct continuous images at arbitrary coordinates and can be applied to any image dataset. Combined with a discrete generative model it becomes a functional generator which can act as a prior in continuous ill-posed inverse problems. We show that FunkNN generates high-quality continuous images and exhibits strong out-of-distribution performance thanks to its patch-based design. We further showcase its performance in several stylized inverse problems with exact spatial derivatives.

Deep Variational Inverse Scattering

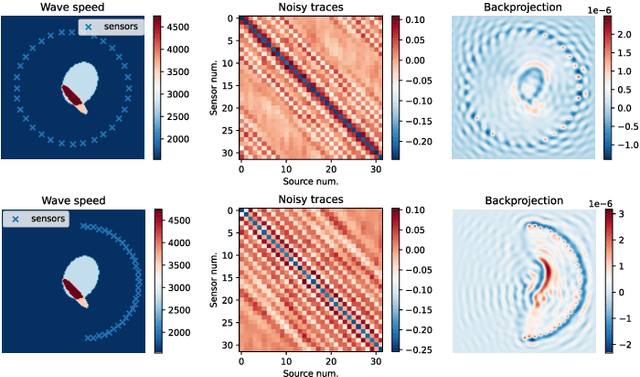
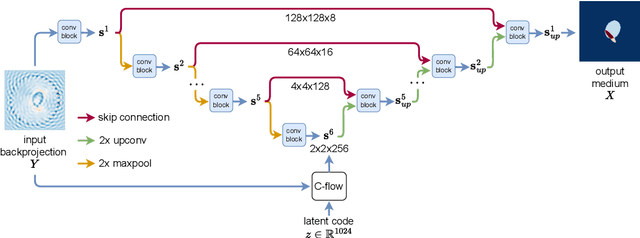
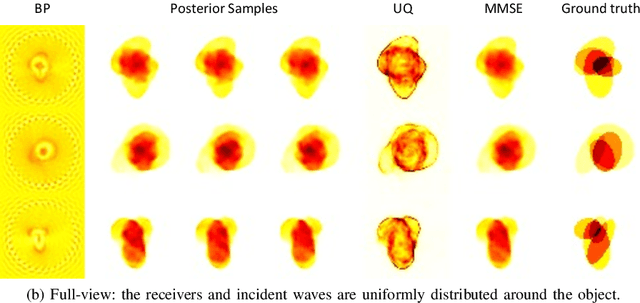
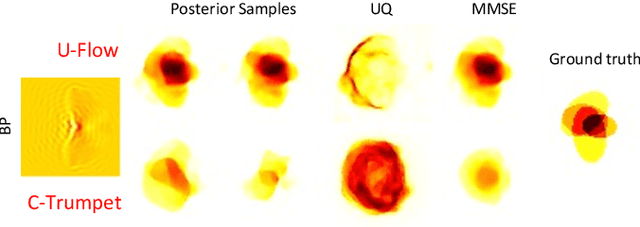
Inverse medium scattering solvers generally reconstruct a single solution without an associated measure of uncertainty. This is true both for the classical iterative solvers and for the emerging deep learning methods. But ill-posedness and noise can make this single estimate inaccurate or misleading. While deep networks such as conditional normalizing flows can be used to sample posteriors in inverse problems, they often yield low-quality samples and uncertainty estimates. In this paper, we propose U-Flow, a Bayesian U-Net based on conditional normalizing flows, which generates high-quality posterior samples and estimates physically-meaningful uncertainty. We show that the proposed model significantly outperforms the recent normalizing flows in terms of posterior sample quality while having comparable performance with the U-Net in point estimation.

Conditional Injective Flows for Bayesian Imaging

Most deep learning models for computational imaging regress a single reconstructed image. In practice, however, ill-posedness, nonlinearity, model mismatch, and noise often conspire to make such point estimates misleading or insufficient. The Bayesian approach models images and (noisy) measurements as jointly distributed random vectors and aims to approximate the posterior distribution of unknowns. Recent variational inference methods based on conditional normalizing flows are a promising alternative to traditional MCMC methods, but they come with drawbacks: excessive memory and compute demands for moderate to high resolution images and underwhelming performance on hard nonlinear problems. In this work, we propose C-Trumpets -- conditional injective flows specifically designed for imaging problems, which greatly diminish these challenges. Injectivity reduces memory footprint and training time while low-dimensional latent space together with architectural innovations like fixed-volume-change layers and skip-connection revnet layers, C-Trumpets outperform regular conditional flow models on a variety of imaging and image restoration tasks, including limited-view CT and nonlinear inverse scattering, with a lower compute and memory budget. C-Trumpets enable fast approximation of point estimates like MMSE or MAP as well as physically-meaningful uncertainty quantification.

Trumpets: Injective Flows for Inference and Inverse Problems

We propose injective generative models called Trumpets that generalize invertible normalizing flows. The proposed generators progressively increase dimension from a low-dimensional latent space. We demonstrate that Trumpets can be trained orders of magnitudes faster than standard flows while yielding samples of comparable or better quality. They retain many of the advantages of the standard flows such as training based on maximum likelihood and a fast, exact inverse of the generator. Since Trumpets are injective and have fast inverses, they can be effectively used for downstream Bayesian inference. To wit, we use Trumpet priors for maximum a posteriori estimation in the context of image reconstruction from compressive measurements, outperforming competitive baselines in terms of reconstruction quality and speed. We then propose an efficient method for posterior characterization and uncertainty quantification with Trumpets by taking advantage of the low-dimensional latent space.