RiNALMo: General-Purpose RNA Language Models Can Generalize Well on Structure Prediction Tasks

Ribonucleic acid (RNA) plays a variety of crucial roles in fundamental biological processes. Recently, RNA has become an interesting drug target, emphasizing the need to improve our understanding of its structures and functions. Over the years, sequencing technologies have produced an enormous amount of unlabeled RNA data, which hides important knowledge and potential. Motivated by the successes of protein language models, we introduce RiboNucleic Acid Language Model (RiNALMo) to help unveil the hidden code of RNA. RiNALMo is the largest RNA language model to date with $650$ million parameters pre-trained on $36$ million non-coding RNA sequences from several available databases. RiNALMo is able to extract hidden knowledge and capture the underlying structure information implicitly embedded within the RNA sequences. RiNALMo achieves state-of-the-art results on several downstream tasks. Notably, we show that its generalization capabilities can overcome the inability of other deep learning methods for secondary structure prediction to generalize on unseen RNA families. The code has been made publicly available on https://github.com/lbcb-sci/RiNALMo.

Estimating Uncertainty in PET Image Reconstruction via Deep Posterior Sampling

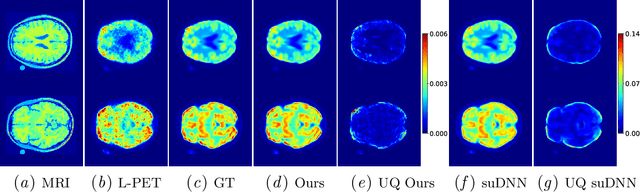
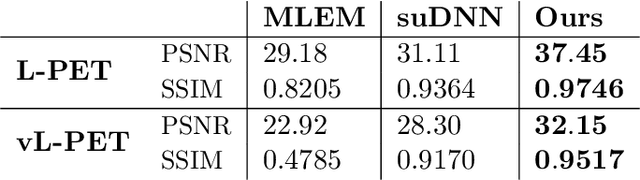
Positron emission tomography (PET) is an important functional medical imaging technique often used in the evaluation of certain brain disorders, whose reconstruction problem is ill-posed. The vast majority of reconstruction methods in PET imaging, both iterative and deep learning, return a single estimate without quantifying the associated uncertainty. Due to ill-posedness and noise, a single solution can be misleading or inaccurate. Thus, providing a measure of uncertainty in PET image reconstruction can help medical practitioners in making critical decisions. This paper proposes a deep learning-based method for uncertainty quantification in PET image reconstruction via posterior sampling. The method is based on training a conditional generative adversarial network whose generator approximates sampling from the posterior in Bayesian inversion. The generator is conditioned on reconstruction from a low-dose PET scan obtained by a conventional reconstruction method and a high-quality magnetic resonance image and learned to estimate a corresponding standard-dose PET scan reconstruction. We show that the proposed model generates high-quality posterior samples and yields physically-meaningful uncertainty estimates.

Deep Variational Inverse Scattering

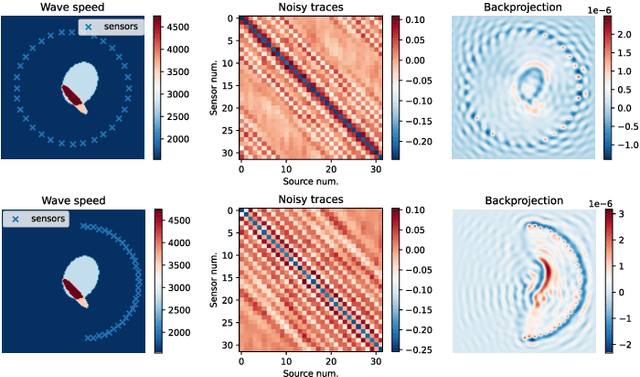
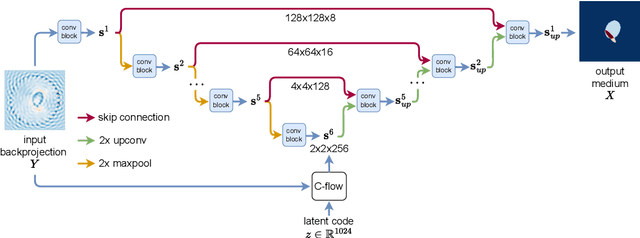
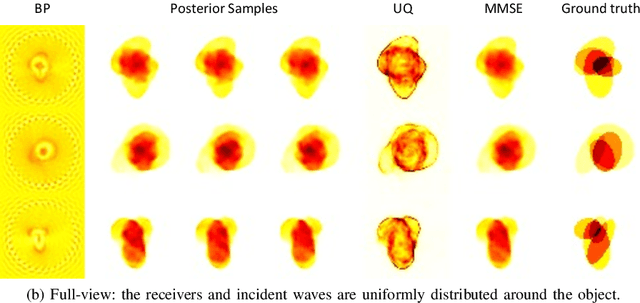
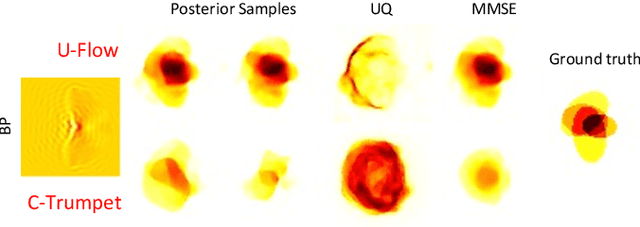
Inverse medium scattering solvers generally reconstruct a single solution without an associated measure of uncertainty. This is true both for the classical iterative solvers and for the emerging deep learning methods. But ill-posedness and noise can make this single estimate inaccurate or misleading. While deep networks such as conditional normalizing flows can be used to sample posteriors in inverse problems, they often yield low-quality samples and uncertainty estimates. In this paper, we propose U-Flow, a Bayesian U-Net based on conditional normalizing flows, which generates high-quality posterior samples and estimates physically-meaningful uncertainty. We show that the proposed model significantly outperforms the recent normalizing flows in terms of posterior sample quality while having comparable performance with the U-Net in point estimation.

Implicit Neural Representation for Mesh-Free Inverse Obstacle Scattering

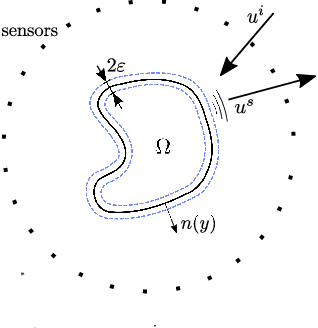
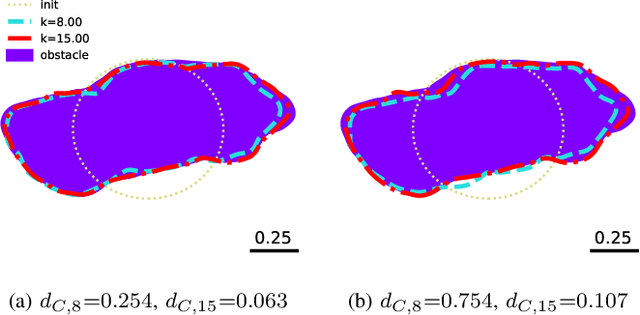
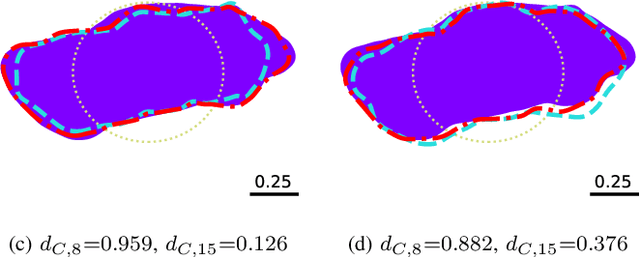
Implicit representation of shapes as level sets of multilayer perceptrons has recently flourished in different shape analysis, compression, and reconstruction tasks. In this paper, we introduce an implicit neural representation-based framework for solving the inverse obstacle scattering problem in a mesh-free fashion. We efficiently express the obstacle shape as the zero-level set of a signed distance function which is implicitly determined by a small number of network parameters. To solve the direct scattering problem, we implement the implicit boundary integral method. It uses projections of the grid points in the tubular neighborhood onto the boundary to compute the PDE solution instead of a grid-size-dependent extraction method of surface points such as Marching Cubes. The implicit representation conveniently handles the shape perturbation in the optimization process. To update the shape, we use PyTorch's automatic differentiation to backpropagate the loss function w.r.t. the network parameters, allowing us to avoid complex and error-prone manual derivation of the shape derivative. The proposed framework makes the inverse scattering problem more tractable with fewer parameters to optimize in comparison to the memory-inefficient grid-based approaches and outputs high-quality reconstruction results.

Single-Pixel Compressive Imaging in Shift-Invariant Spaces via Exact Wavelet Frames

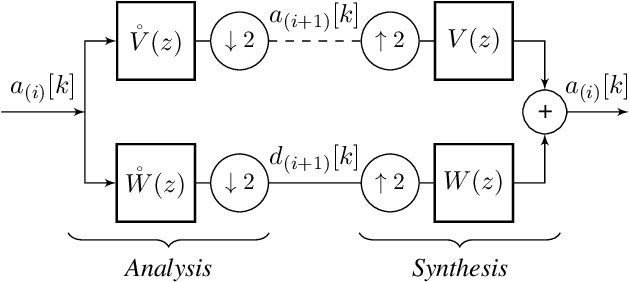
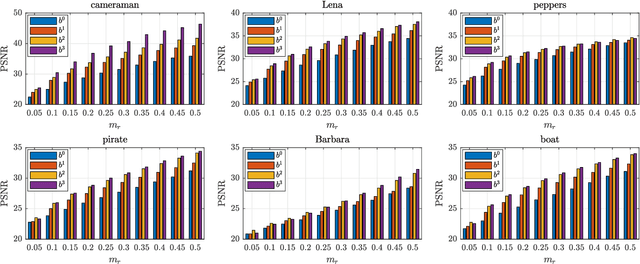
This paper introduces a novel framework for single-pixel imaging via compressive sensing (CS) in shift-invariant (SI) spaces by exploiting the sparsity property of a wavelet representation. We reinterpret the acquisition procedure of a single-pixel camera as filtering of the observed signal with continuous-domain functions that lie in an SI subspace spanned by the integer shifts of the box function. The signal is modeled by an arbitrary SI generator whose special case is the box function, which, as we show in the paper, is conventionally used in single-pixel imaging. We propose to use separable B-spline generators which are intuitively complemented by sparsity-inducing spline wavelets. The SI models of the acquisition and the underlying signal lead to an exact discretization of an inherently continuous-domain inverse problem to a finite-dimensional problem of CS type. By solving the CS optimization problem, a parametric representation of the signal is obtained. Such a representation offers many practical advantages in image processing applications. We propose an efficient matrix-free implementation of the framework and conduct it on the standard test images and real-world measurement data. Experimental results show that the proposed framework achieves a significant improvement of the reconstruction quality relative to the conventional CS setting.