Deep Variational Inverse Scattering
Paper and Code
Dec 09, 2022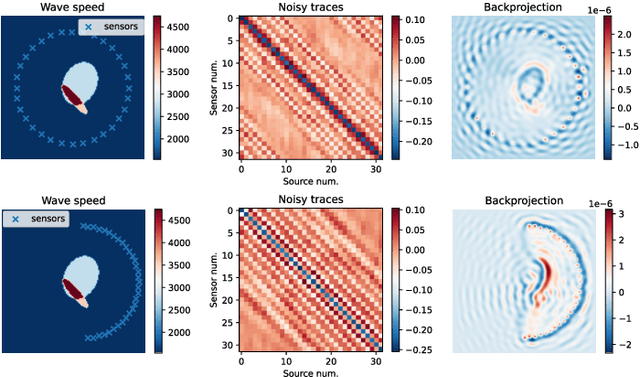
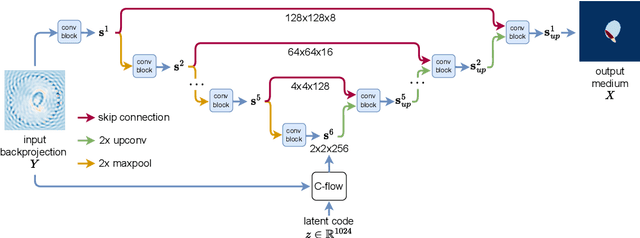
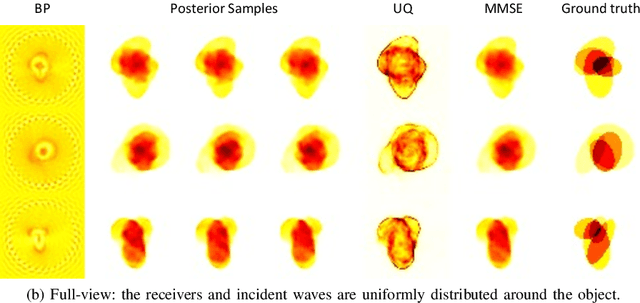
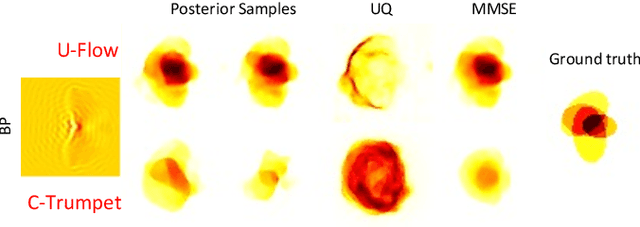
Inverse medium scattering solvers generally reconstruct a single solution without an associated measure of uncertainty. This is true both for the classical iterative solvers and for the emerging deep learning methods. But ill-posedness and noise can make this single estimate inaccurate or misleading. While deep networks such as conditional normalizing flows can be used to sample posteriors in inverse problems, they often yield low-quality samples and uncertainty estimates. In this paper, we propose U-Flow, a Bayesian U-Net based on conditional normalizing flows, which generates high-quality posterior samples and estimates physically-meaningful uncertainty. We show that the proposed model significantly outperforms the recent normalizing flows in terms of posterior sample quality while having comparable performance with the U-Net in point estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge