Single-Pixel Compressive Imaging in Shift-Invariant Spaces via Exact Wavelet Frames

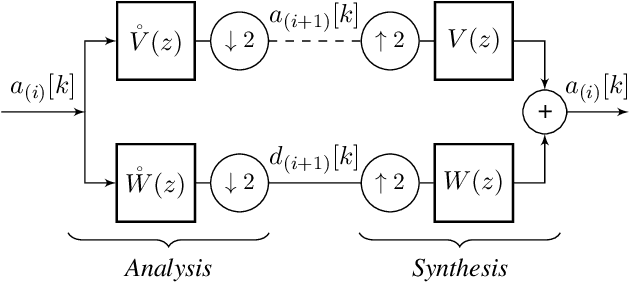
This paper introduces a novel framework for single-pixel imaging via compressive sensing (CS) in shift-invariant (SI) spaces by exploiting the sparsity property of a wavelet representation. We reinterpret the acquisition procedure of a single-pixel camera as filtering of the observed signal with continuous-domain functions that lie in an SI subspace spanned by the integer shifts of the box function. The signal is modeled by an arbitrary SI generator whose special case is the box function, which, as we show in the paper, is conventionally used in single-pixel imaging. We propose to use separable B-spline generators which are intuitively complemented by sparsity-inducing spline wavelets. The SI models of the acquisition and the underlying signal lead to an exact discretization of an inherently continuous-domain inverse problem to a finite-dimensional problem of CS type. By solving the CS optimization problem, a parametric representation of the signal is obtained. Such a representation offers many practical advantages in image processing applications. We propose an efficient matrix-free implementation of the framework and conduct it on the standard test images and real-world measurement data. Experimental results show that the proposed framework achieves a significant improvement of the reconstruction quality relative to the conventional CS setting.