Accurate 2D Reconstruction for PET Scanners based on the Analytical White Image Model

In this paper, we provide a precise mathematical model of crystal-to-crystal response which is used to generate the white image - a necessary compensation model needed to overcome the physical limitations of the PET scanner. We present a closed-form solution, as well as several accurate approximations, due to the complexity of the exact mathematical expressions. We prove, experimentally and analytically, that the difference between the best approximations and real crystal-to-crystal response is insignificant. The obtained responses are used to generate the white image compensation model. It can be written as a single closed-form expression making it easy to implement in known reconstruction methods. The maximum likelihood expectation maximization (MLEM) algorithm is modified and our white image model is integrated into it. The modified MLEM algorithm is not based on the system matrix, rather it is based on ray-driven projections and back-projections. The compensation model provides all necessary information about the system. Finally, we check our approach on synthetic and real data. For the real-world acquisition, we use the Raytest ClearPET camera for small animals and the NEMA NU 4-2008 phantom. The proposed approach overperforms competitive, non-compensated reconstruction methods.

Accurate PET Reconstruction from Reduced Set of Measurements based on GMM

In this paper, we provide a novel method for the estimation of unknown parameters of the Gaussian Mixture Model (GMM) in Positron Emission Tomography (PET). A vast majority of PET imaging methods are based on reconstruction model that is defined by values on some pixel/voxel grid. Instead, we propose a continuous parametric GMM model. Usually, Expectation-Maximization (EM) iterations are used to obtain the GMM model parameters from some set of point-wise measurements. The challenge of PET reconstruction is that the measurement is represented by the so called lines of response (LoR), instead of points. The goal is to estimate the unknown parameters of the Gaussian mixture directly from a relatively small set of LoR-s. Estimation of unknown parameters relies on two facts: the marginal distribution theorem of the multivariate normal distribution; and the properties of the marginal distribution of LoR-s. We propose an iterative algorithm that resembles the maximum-likelihood method to determine the unknown parameters. Results show that the estimated parameters follow the correct ones with a great accuracy. The result is promising, since the high-quality parametric reconstruction model can be obtained from lower dose measurements, and is directly suitable for further processing.

Estimating Uncertainty in PET Image Reconstruction via Deep Posterior Sampling

Positron emission tomography (PET) is an important functional medical imaging technique often used in the evaluation of certain brain disorders, whose reconstruction problem is ill-posed. The vast majority of reconstruction methods in PET imaging, both iterative and deep learning, return a single estimate without quantifying the associated uncertainty. Due to ill-posedness and noise, a single solution can be misleading or inaccurate. Thus, providing a measure of uncertainty in PET image reconstruction can help medical practitioners in making critical decisions. This paper proposes a deep learning-based method for uncertainty quantification in PET image reconstruction via posterior sampling. The method is based on training a conditional generative adversarial network whose generator approximates sampling from the posterior in Bayesian inversion. The generator is conditioned on reconstruction from a low-dose PET scan obtained by a conventional reconstruction method and a high-quality magnetic resonance image and learned to estimate a corresponding standard-dose PET scan reconstruction. We show that the proposed model generates high-quality posterior samples and yields physically-meaningful uncertainty estimates.

Single-Pixel Compressive Imaging in Shift-Invariant Spaces via Exact Wavelet Frames

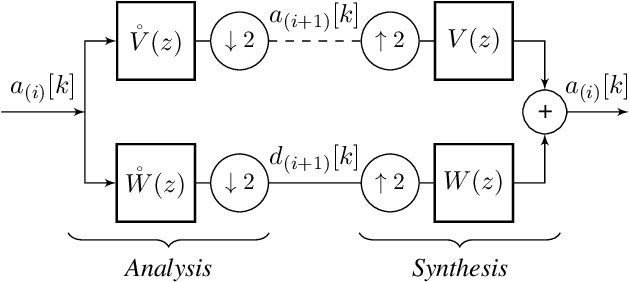
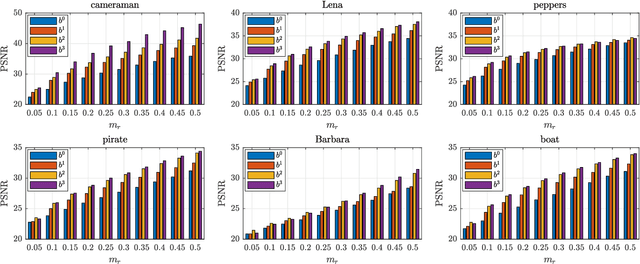
This paper introduces a novel framework for single-pixel imaging via compressive sensing (CS) in shift-invariant (SI) spaces by exploiting the sparsity property of a wavelet representation. We reinterpret the acquisition procedure of a single-pixel camera as filtering of the observed signal with continuous-domain functions that lie in an SI subspace spanned by the integer shifts of the box function. The signal is modeled by an arbitrary SI generator whose special case is the box function, which, as we show in the paper, is conventionally used in single-pixel imaging. We propose to use separable B-spline generators which are intuitively complemented by sparsity-inducing spline wavelets. The SI models of the acquisition and the underlying signal lead to an exact discretization of an inherently continuous-domain inverse problem to a finite-dimensional problem of CS type. By solving the CS optimization problem, a parametric representation of the signal is obtained. Such a representation offers many practical advantages in image processing applications. We propose an efficient matrix-free implementation of the framework and conduct it on the standard test images and real-world measurement data. Experimental results show that the proposed framework achieves a significant improvement of the reconstruction quality relative to the conventional CS setting.