Anadi Chaman
University of Illinois at Urbana-Champaign
FunkNN: Neural Interpolation for Functional Generation
Dec 20, 2022Abstract:Can we build continuous generative models which generalize across scales, can be evaluated at any coordinate, admit calculation of exact derivatives, and are conceptually simple? Existing MLP-based architectures generate worse samples than the grid-based generators with favorable convolutional inductive biases. Models that focus on generating images at different scales do better, but employ complex architectures not designed for continuous evaluation of images and derivatives. We take a signal-processing perspective and treat continuous image generation as interpolation from samples. Indeed, correctly sampled discrete images contain all information about the low spatial frequencies. The question is then how to extrapolate the spectrum in a data-driven way while meeting the above design criteria. Our answer is FunkNN -- a new convolutional network which learns how to reconstruct continuous images at arbitrary coordinates and can be applied to any image dataset. Combined with a discrete generative model it becomes a functional generator which can act as a prior in continuous ill-posed inverse problems. We show that FunkNN generates high-quality continuous images and exhibits strong out-of-distribution performance thanks to its patch-based design. We further showcase its performance in several stylized inverse problems with exact spatial derivatives.
Truly shift-equivariant convolutional neural networks with adaptive polyphase upsampling
May 09, 2021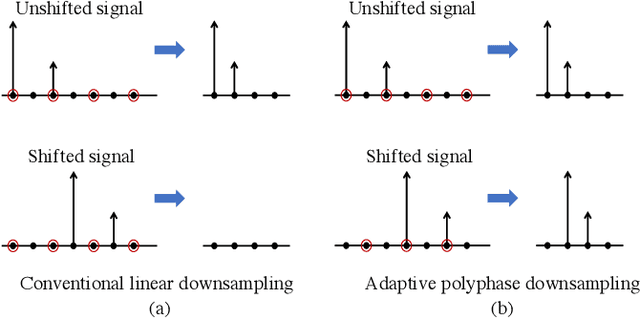
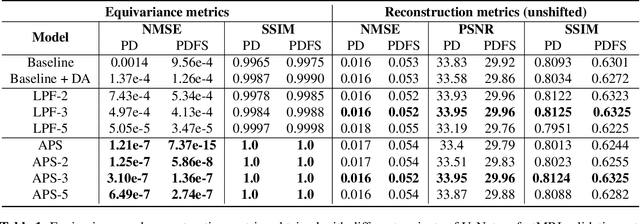
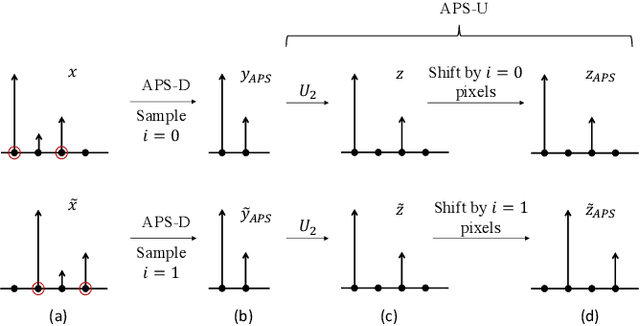

Abstract:Convolutional neural networks lack shift equivariance due to the presence of downsampling layers. In image classification, adaptive polyphase downsampling (APS-D) was recently proposed to make CNNs perfectly shift invariant. However, in networks used for image reconstruction tasks, it can not by itself restore shift equivariance. We address this problem by proposing adaptive polyphase upsampling (APS-U), a non-linear extension of conventional upsampling, which allows CNNs to exhibit perfect shift equivariance. With MRI and CT reconstruction experiments, we show that networks containing APS-D/U layers exhibit state of the art equivariance performance without sacrificing on image reconstruction quality. In addition, unlike prior methods like data augmentation and anti-aliasing, the gains in equivariance obtained from APS-D/U also extend to images outside the training distribution.
Truly shift-invariant convolutional neural networks
Dec 04, 2020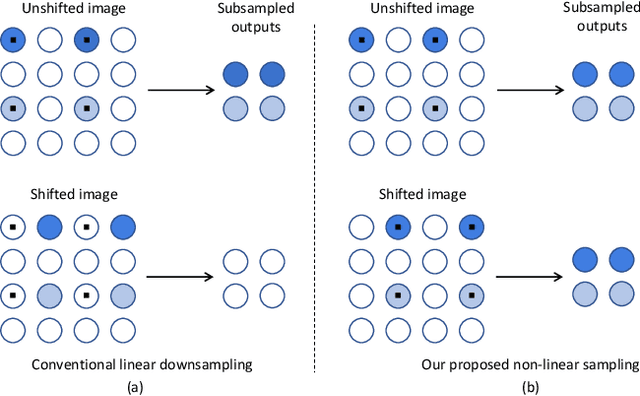
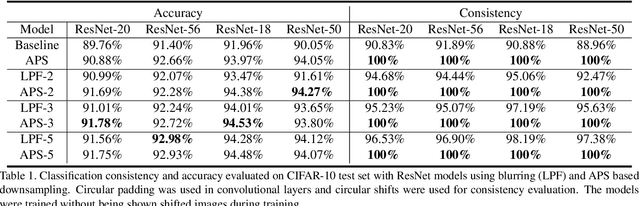
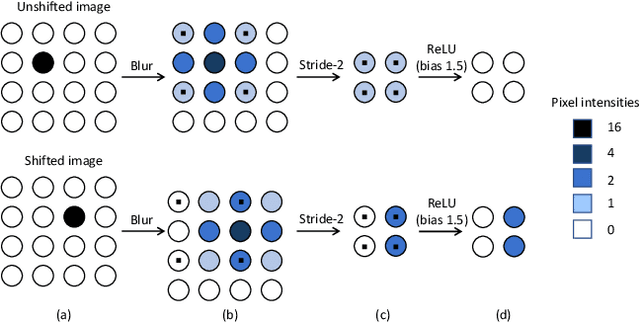
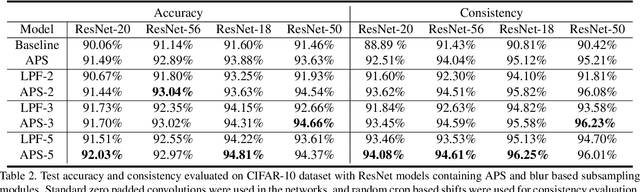
Abstract:Thanks to the use of convolution and pooling layers, convolutional neural networks were for a long time thought to be shift-invariant. However, recent works have shown that the output of a CNN can change significantly with small shifts in input: a problem caused by the presence of downsampling (stride) layers. The existing solutions rely either on data augmentation or on anti-aliasing, both of which have limitations and neither of which enables perfect shift invariance. Additionally, the gains obtained from these methods do not extend to image patterns not seen during training. To address these challenges, we propose adaptive polyphase sampling (APS), a simple sub-sampling scheme that allows convolutional neural networks to achieve 100% consistency in classification performance under shifts, without any loss in accuracy. With APS the networks exhibit perfect consistency to shifts even before training, making it the first approach that makes convolutional neural networks truly shift invariant.
Interpreting U-Nets via Task-Driven Multiscale Dictionary Learning
Nov 25, 2020
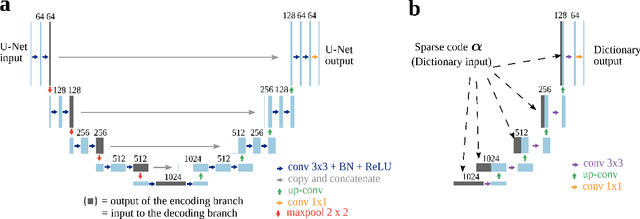


Abstract:U-Nets have been tremendously successful in many imaging inverse problems. In an effort to understand the source of this success, we show that one can reduce a U-Net to a tractable, well-understood sparsity-driven dictionary model while retaining its strong empirical performance. We achieve this by extracting a certain multiscale convolutional dictionary from the standard U-Net. This dictionary imitates the structure of the U-Net in its convolution, scale-separation, and skip connection aspects, while doing away with the nonlinear parts. We show that this model can be trained in a task-driven dictionary learning framework and yield comparable results to standard U-Nets on a number of relevant tasks, including CT and MRI reconstruction. These results suggest that the success of the U-Net may be explained mainly by its multiscale architecture and the induced sparse representation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge