A Comprehensive Analysis on the Learning Curve in Kernel Ridge Regression

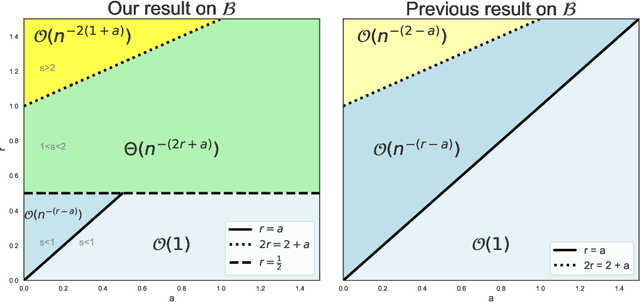
This paper conducts a comprehensive study of the learning curves of kernel ridge regression (KRR) under minimal assumptions. Our contributions are three-fold: 1) we analyze the role of key properties of the kernel, such as its spectral eigen-decay, the characteristics of the eigenfunctions, and the smoothness of the kernel; 2) we demonstrate the validity of the Gaussian Equivalent Property (GEP), which states that the generalization performance of KRR remains the same when the whitened features are replaced by standard Gaussian vectors, thereby shedding light on the success of previous analyzes under the Gaussian Design Assumption; 3) we derive novel bounds that improve over existing bounds across a broad range of setting such as (in)dependent feature vectors and various combinations of eigen-decay rates in the over/underparameterized regimes.

Characterizing Overfitting in Kernel Ridgeless Regression Through the Eigenspectrum

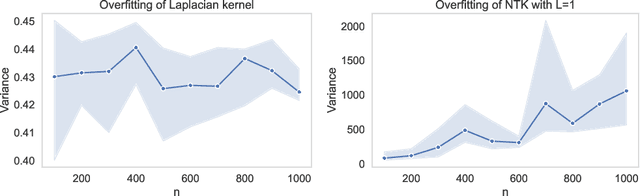
We derive new bounds for the condition number of kernel matrices, which we then use to enhance existing non-asymptotic test error bounds for kernel ridgeless regression in the over-parameterized regime for a fixed input dimension. For kernels with polynomial spectral decay, we recover the bound from previous work; for exponential decay, our bound is non-trivial and novel. Our conclusion on overfitting is two-fold: (i) kernel regressors whose eigenspectrum decays polynomially must generalize well, even in the presence of noisy labeled training data; these models exhibit so-called tempered overfitting; (ii) if the eigenspectrum of any kernel ridge regressor decays exponentially, then it generalizes poorly, i.e., it exhibits catastrophic overfitting. This adds to the available characterization of kernel ridge regressors exhibiting benign overfitting as the extremal case where the eigenspectrum of the kernel decays sub-polynomially. Our analysis combines new random matrix theory (RMT) techniques with recent tools in the kernel ridge regression (KRR) literature.

A Theoretical Analysis of the Test Error of Finite-Rank Kernel Ridge Regression

Existing statistical learning guarantees for general kernel regressors often yield loose bounds when used with finite-rank kernels. Yet, finite-rank kernels naturally appear in several machine learning problems, e.g.\ when fine-tuning a pre-trained deep neural network's last layer to adapt it to a novel task when performing transfer learning. We address this gap for finite-rank kernel ridge regression (KRR) by deriving sharp non-asymptotic upper and lower bounds for the KRR test error of any finite-rank KRR. Our bounds are tighter than previously derived bounds on finite-rank KRR, and unlike comparable results, they also remain valid for any regularization parameters.

Injectivity of ReLU networks: perspectives from statistical physics

When can the input of a ReLU neural network be inferred from its output? In other words, when is the network injective? We consider a single layer, $x \mapsto \mathrm{ReLU}(Wx)$, with a random Gaussian $m \times n$ matrix $W$, in a high-dimensional setting where $n, m \to \infty$. Recent work connects this problem to spherical integral geometry giving rise to a conjectured sharp injectivity threshold for $\alpha = \frac{m}{n}$ by studying the expected Euler characteristic of a certain random set. We adopt a different perspective and show that injectivity is equivalent to a property of the ground state of the spherical perceptron, an important spin glass model in statistical physics. By leveraging the (non-rigorous) replica symmetry-breaking theory, we derive analytical equations for the threshold whose solution is at odds with that from the Euler characteristic. Furthermore, we use Gordon's min--max theorem to prove that a replica-symmetric upper bound refutes the Euler characteristic prediction. Along the way we aim to give a tutorial-style introduction to key ideas from statistical physics in an effort to make the exposition accessible to a broad audience. Our analysis establishes a connection between spin glasses and integral geometry but leaves open the problem of explaining the discrepancies.

Interpreting U-Nets via Task-Driven Multiscale Dictionary Learning

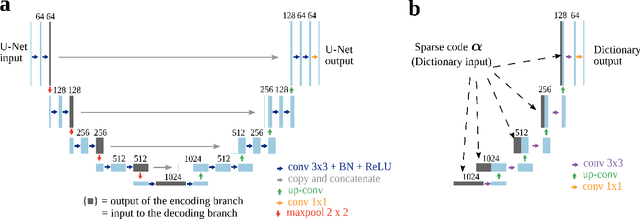
U-Nets have been tremendously successful in many imaging inverse problems. In an effort to understand the source of this success, we show that one can reduce a U-Net to a tractable, well-understood sparsity-driven dictionary model while retaining its strong empirical performance. We achieve this by extracting a certain multiscale convolutional dictionary from the standard U-Net. This dictionary imitates the structure of the U-Net in its convolution, scale-separation, and skip connection aspects, while doing away with the nonlinear parts. We show that this model can be trained in a task-driven dictionary learning framework and yield comparable results to standard U-Nets on a number of relevant tasks, including CT and MRI reconstruction. These results suggest that the success of the U-Net may be explained mainly by its multiscale architecture and the induced sparse representation.

On the Empirical Neural Tangent Kernel of Standard Finite-Width Convolutional Neural Network Architectures

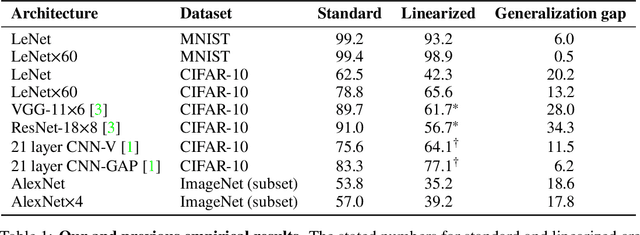
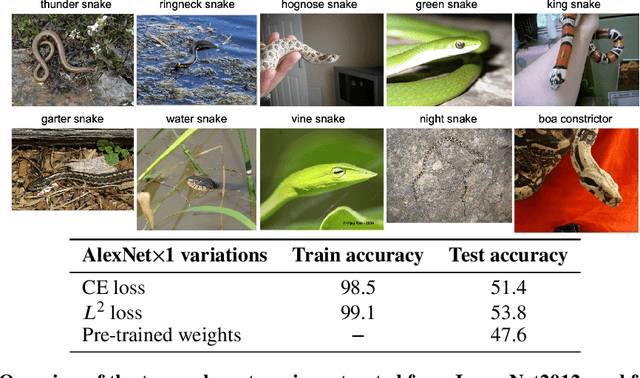
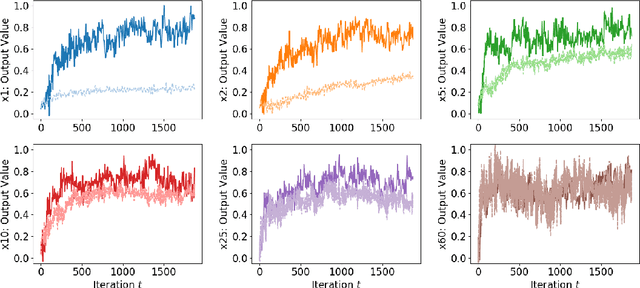
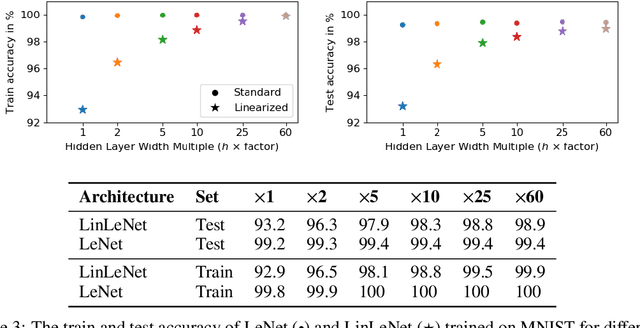
The Neural Tangent Kernel (NTK) is an important milestone in the ongoing effort to build a theory for deep learning. Its prediction that sufficiently wide neural networks behave as kernel methods, or equivalently as random feature models, has been confirmed empirically for certain wide architectures. It remains an open question how well NTK theory models standard neural network architectures of widths common in practice, trained on complex datasets such as ImageNet. We study this question empirically for two well-known convolutional neural network architectures, namely AlexNet and LeNet, and find that their behavior deviates significantly from their finite-width NTK counterparts. For wider versions of these networks, where the number of channels and widths of fully-connected layers are increased, the deviation decreases.