A Comprehensive Analysis on the Learning Curve in Kernel Ridge Regression

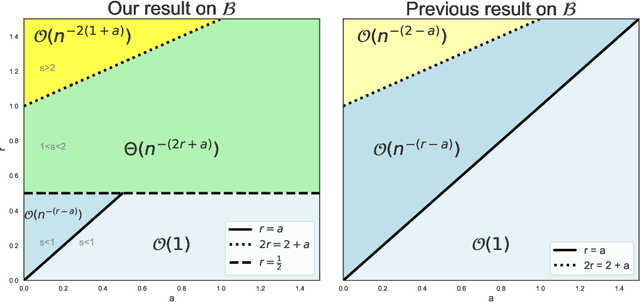
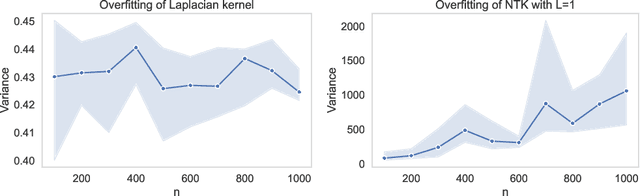
This paper conducts a comprehensive study of the learning curves of kernel ridge regression (KRR) under minimal assumptions. Our contributions are three-fold: 1) we analyze the role of key properties of the kernel, such as its spectral eigen-decay, the characteristics of the eigenfunctions, and the smoothness of the kernel; 2) we demonstrate the validity of the Gaussian Equivalent Property (GEP), which states that the generalization performance of KRR remains the same when the whitened features are replaced by standard Gaussian vectors, thereby shedding light on the success of previous analyzes under the Gaussian Design Assumption; 3) we derive novel bounds that improve over existing bounds across a broad range of setting such as (in)dependent feature vectors and various combinations of eigen-decay rates in the over/underparameterized regimes.

Characterizing Overfitting in Kernel Ridgeless Regression Through the Eigenspectrum

We derive new bounds for the condition number of kernel matrices, which we then use to enhance existing non-asymptotic test error bounds for kernel ridgeless regression in the over-parameterized regime for a fixed input dimension. For kernels with polynomial spectral decay, we recover the bound from previous work; for exponential decay, our bound is non-trivial and novel. Our conclusion on overfitting is two-fold: (i) kernel regressors whose eigenspectrum decays polynomially must generalize well, even in the presence of noisy labeled training data; these models exhibit so-called tempered overfitting; (ii) if the eigenspectrum of any kernel ridge regressor decays exponentially, then it generalizes poorly, i.e., it exhibits catastrophic overfitting. This adds to the available characterization of kernel ridge regressors exhibiting benign overfitting as the extremal case where the eigenspectrum of the kernel decays sub-polynomially. Our analysis combines new random matrix theory (RMT) techniques with recent tools in the kernel ridge regression (KRR) literature.

A Theoretical Analysis of the Test Error of Finite-Rank Kernel Ridge Regression

Existing statistical learning guarantees for general kernel regressors often yield loose bounds when used with finite-rank kernels. Yet, finite-rank kernels naturally appear in several machine learning problems, e.g.\ when fine-tuning a pre-trained deep neural network's last layer to adapt it to a novel task when performing transfer learning. We address this gap for finite-rank kernel ridge regression (KRR) by deriving sharp non-asymptotic upper and lower bounds for the KRR test error of any finite-rank KRR. Our bounds are tighter than previously derived bounds on finite-rank KRR, and unlike comparable results, they also remain valid for any regularization parameters.