LoRA Fine-Tuning Without GPUs: A CPU-Efficient Meta-Generation Framework for LLMs

Low-Rank Adapters (LoRAs) have transformed the fine-tuning of Large Language Models (LLMs) by enabling parameter-efficient updates. However, their widespread adoption remains limited by the reliance on GPU-based training. In this work, we propose a theoretically grounded approach to LoRA fine-tuning designed specifically for users with limited computational resources, particularly those restricted to standard laptop CPUs. Our method learns a meta-operator that maps any input dataset, represented as a probability distribution, to a set of LoRA weights by leveraging a large bank of pre-trained adapters for the Mistral-7B-Instruct-v0.2 model. Instead of performing new gradient-based updates, our pipeline constructs adapters via lightweight combinations of existing LoRAs directly on CPU. While the resulting adapters do not match the performance of GPU-trained counterparts, they consistently outperform the base Mistral model on downstream tasks, offering a practical and accessible alternative to traditional GPU-based fine-tuning.

Sharp Generalization Bounds for Foundation Models with Asymmetric Randomized Low-Rank Adapters

Low-Rank Adaptation (LoRA) has emerged as a widely adopted parameter-efficient fine-tuning (PEFT) technique for foundation models. Recent work has highlighted an inherent asymmetry in the initialization of LoRA's low-rank factors, which has been present since its inception and was presumably derived experimentally. This paper focuses on providing a comprehensive theoretical characterization of asymmetric LoRA with frozen random factors. First, while existing research provides upper-bound generalization guarantees based on averages over multiple experiments, the behaviour of a single fine-tuning run with specific random factors remains an open question. We address this by investigating the concentration of the typical LoRA generalization gap around its mean. Our main upper bound reveals a sample complexity of $\tilde{\mathcal{O}}\left(\frac{\sqrt{r}}{\sqrt{N}}\right)$ with high probability for rank $r$ LoRAs trained on $N$ samples. Additionally, we also determine the fundamental limits in terms of sample efficiency, establishing a matching lower bound of $\mathcal{O}\left(\frac{1}{\sqrt{N}}\right)$. By more closely reflecting the practical scenario of a single fine-tuning run, our findings offer crucial insights into the reliability and practicality of asymmetric LoRA.

Fine-Tuning Next-Scale Visual Autoregressive Models with Group Relative Policy Optimization

Fine-tuning pre-trained generative models with Reinforcement Learning (RL) has emerged as an effective approach for aligning outputs more closely with nuanced human preferences. In this paper, we investigate the application of Group Relative Policy Optimization (GRPO) to fine-tune next-scale visual autoregressive (VAR) models. Our empirical results demonstrate that this approach enables alignment to intricate reward signals derived from aesthetic predictors and CLIP embeddings, significantly enhancing image quality and enabling precise control over the generation style. Interestingly, by leveraging CLIP, our method can help VAR models generalize beyond their initial ImageNet distribution: through RL-driven exploration, these models can generate images aligned with prompts referencing image styles that were absent during pre-training. In summary, we show that RL-based fine-tuning is both efficient and effective for VAR models, benefiting particularly from their fast inference speeds, which are advantageous for online sampling, an aspect that poses significant challenges for diffusion-based alternatives.

Towards Quantifying Long-Range Interactions in Graph Machine Learning: a Large Graph Dataset and a Measurement

Long-range dependencies are critical for effective graph representation learning, yet most existing datasets focus on small graphs tailored to inductive tasks, offering limited insight into long-range interactions. Current evaluations primarily compare models employing global attention (e.g., graph transformers) with those using local neighborhood aggregation (e.g., message-passing neural networks) without a direct measurement of long-range dependency. In this work, we introduce City-Networks, a novel large-scale transductive learning dataset derived from real-world city roads. This dataset features graphs with over $10^5$ nodes and significantly larger diameters than those in existing benchmarks, naturally embodying long-range information. We annotate the graphs using an eccentricity-based approach, ensuring that the classification task inherently requires information from distant nodes. Furthermore, we propose a model-agnostic measurement based on the Jacobians of neighbors from distant hops, offering a principled quantification of long-range dependencies. Finally, we provide theoretical justifications for both our dataset design and the proposed measurement - particularly by focusing on over-smoothing and influence score dilution - which establishes a robust foundation for further exploration of long-range interactions in graph neural networks.

Keep It Light! Simplifying Image Clustering Via Text-Free Adapters

Many competitive clustering pipelines have a multi-modal design, leveraging large language models (LLMs) or other text encoders, and text-image pairs, which are often unavailable in real-world downstream applications. Additionally, such frameworks are generally complicated to train and require substantial computational resources, making widespread adoption challenging. In this work, we show that in deep clustering, competitive performance with more complex state-of-the-art methods can be achieved using a text-free and highly simplified training pipeline. In particular, our approach, Simple Clustering via Pre-trained models (SCP), trains only a small cluster head while leveraging pre-trained vision model feature representations and positive data pairs. Experiments on benchmark datasets including CIFAR-10, CIFAR-20, CIFAR-100, STL-10, ImageNet-10, and ImageNet-Dogs, demonstrate that SCP achieves highly competitive performance. Furthermore, we provide a theoretical result explaining why, at least under ideal conditions, additional text-based embeddings may not be necessary to achieve strong clustering performance in vision.

Scalable Message Passing Neural Networks: No Need for Attention in Large Graph Representation Learning

We propose Scalable Message Passing Neural Networks (SMPNNs) and demonstrate that, by integrating standard convolutional message passing into a Pre-Layer Normalization Transformer-style block instead of attention, we can produce high-performing deep message-passing-based Graph Neural Networks (GNNs). This modification yields results competitive with the state-of-the-art in large graph transductive learning, particularly outperforming the best Graph Transformers in the literature, without requiring the otherwise computationally and memory-expensive attention mechanism. Our architecture not only scales to large graphs but also makes it possible to construct deep message-passing networks, unlike simple GNNs, which have traditionally been constrained to shallow architectures due to oversmoothing. Moreover, we provide a new theoretical analysis of oversmoothing based on universal approximation which we use to motivate SMPNNs. We show that in the context of graph convolutions, residual connections are necessary for maintaining the universal approximation properties of downstream learners and that removing them can lead to a loss of universality.

Neural Spacetimes for DAG Representation Learning

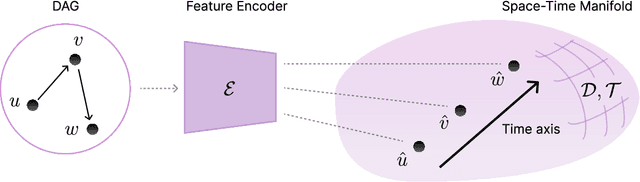
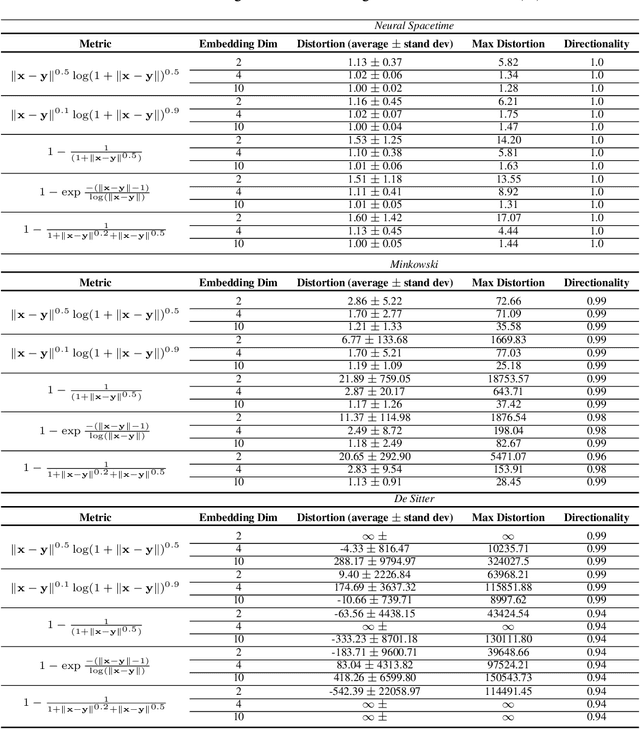
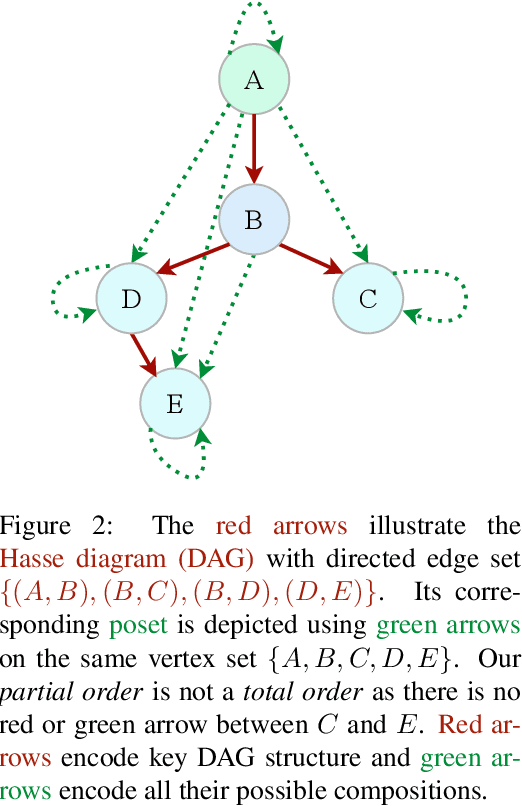
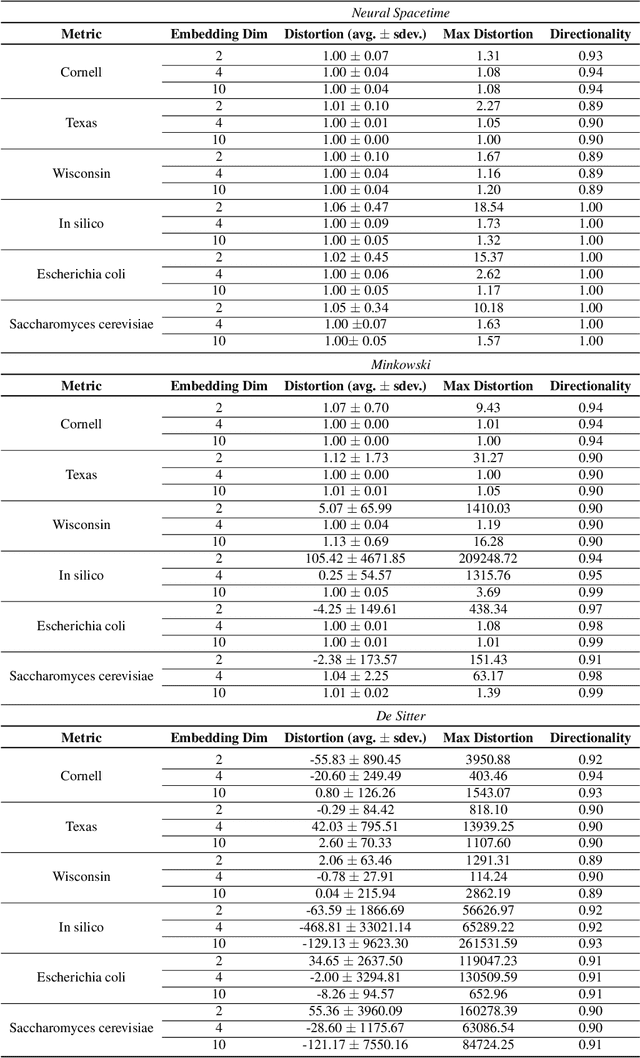
We propose a class of trainable deep learning-based geometries called Neural Spacetimes (NSTs), which can universally represent nodes in weighted directed acyclic graphs (DAGs) as events in a spacetime manifold. While most works in the literature focus on undirected graph representation learning or causality embedding separately, our differentiable geometry can encode both graph edge weights in its spatial dimensions and causality in the form of edge directionality in its temporal dimensions. We use a product manifold that combines a quasi-metric (for space) and a partial order (for time). NSTs are implemented as three neural networks trained in an end-to-end manner: an embedding network, which learns to optimize the location of nodes as events in the spacetime manifold, and two other networks that optimize the space and time geometries in parallel, which we call a neural (quasi-)metric and a neural partial order, respectively. The latter two networks leverage recent ideas at the intersection of fractal geometry and deep learning to shape the geometry of the representation space in a data-driven fashion, unlike other works in the literature that use fixed spacetime manifolds such as Minkowski space or De Sitter space to embed DAGs. Our main theoretical guarantee is a universal embedding theorem, showing that any $k$-point DAG can be embedded into an NST with $1+\mathcal{O}(\log(k))$ distortion while exactly preserving its causal structure. The total number of parameters defining the NST is sub-cubic in $k$ and linear in the width of the DAG. If the DAG has a planar Hasse diagram, this is improved to $\mathcal{O}(\log(k)) + 2)$ spatial and 2 temporal dimensions. We validate our framework computationally with synthetic weighted DAGs and real-world network embeddings; in both cases, the NSTs achieve lower embedding distortions than their counterparts using fixed spacetime geometries.

Metric Learning for Clifford Group Equivariant Neural Networks

Clifford Group Equivariant Neural Networks (CGENNs) leverage Clifford algebras and multivectors as an alternative approach to incorporating group equivariance to ensure symmetry constraints in neural representations. In principle, this formulation generalizes to orthogonal groups and preserves equivariance regardless of the metric signature. However, previous works have restricted internal network representations to Euclidean or Minkowski (pseudo-)metrics, handpicked depending on the problem at hand. In this work, we propose an alternative method that enables the metric to be learned in a data-driven fashion, allowing the CGENN network to learn more flexible representations. Specifically, we populate metric matrices fully, ensuring they are symmetric by construction, and leverage eigenvalue decomposition to integrate this additional learnable component into the original CGENN formulation in a principled manner. Additionally, we motivate our method using insights from category theory, which enables us to explain Clifford algebras as a categorical construction and guarantee the mathematical soundness of our approach. We validate our method in various tasks and showcase the advantages of learning more flexible latent metric representations. The code and data are available at https://github.com/rick-ali/Metric-Learning-for-CGENNs

Score Distillation via Reparametrized DDIM

While 2D diffusion models generate realistic, high-detail images, 3D shape generation methods like Score Distillation Sampling (SDS) built on these 2D diffusion models produce cartoon-like, over-smoothed shapes. To help explain this discrepancy, we show that the image guidance used in Score Distillation can be understood as the velocity field of a 2D denoising generative process, up to the choice of a noise term. In particular, after a change of variables, SDS resembles a high-variance version of Denoising Diffusion Implicit Models (DDIM) with a differently-sampled noise term: SDS introduces noise i.i.d. randomly at each step, while DDIM infers it from the previous noise predictions. This excessive variance can lead to over-smoothing and unrealistic outputs. We show that a better noise approximation can be recovered by inverting DDIM in each SDS update step. This modification makes SDS's generative process for 2D images almost identical to DDIM. In 3D, it removes over-smoothing, preserves higher-frequency detail, and brings the generation quality closer to that of 2D samplers. Experimentally, our method achieves better or similar 3D generation quality compared to other state-of-the-art Score Distillation methods, all without training additional neural networks or multi-view supervision, and providing useful insights into relationship between 2D and 3D asset generation with diffusion models.

Asymmetry in Low-Rank Adapters of Foundation Models

Parameter-efficient fine-tuning optimizes large, pre-trained foundation models by updating a subset of parameters; in this class, Low-Rank Adaptation (LoRA) is particularly effective. Inspired by an effort to investigate the different roles of LoRA matrices during fine-tuning, this paper characterizes and leverages unexpected asymmetry in the importance of low-rank adapter matrices. Specifically, when updating the parameter matrices of a neural network by adding a product $BA$, we observe that the $B$ and $A$ matrices have distinct functions: $A$ extracts features from the input, while $B$ uses these features to create the desired output. Based on this observation, we demonstrate that fine-tuning $B$ is inherently more effective than fine-tuning $A$, and that a random untrained $A$ should perform nearly as well as a fine-tuned one. Using an information-theoretic lens, we also bound the generalization of low-rank adapters, showing that the parameter savings of exclusively training $B$ improves the bound. We support our conclusions with experiments on RoBERTa, BART-Large, LLaMA-2, and ViTs.