Kristjan Greenewald
Private Continuous-Time Synthetic Trajectory Generation via Mean-Field Langevin Dynamics
Jun 13, 2025Abstract:We provide an algorithm to privately generate continuous-time data (e.g. marginals from stochastic differential equations), which has applications in highly sensitive domains involving time-series data such as healthcare. We leverage the connections between trajectory inference and continuous-time synthetic data generation, along with a computational method based on mean-field Langevin dynamics. As discretized mean-field Langevin dynamics and noisy particle gradient descent are equivalent, DP results for noisy SGD can be applied to our setting. We provide experiments that generate realistic trajectories on a synthesized variation of hand-drawn MNIST data while maintaining meaningful privacy guarantees. Crucially, our method has strong utility guarantees under the setting where each person contributes data for \emph{only one time point}, while prior methods require each person to contribute their \emph{entire temporal trajectory}--directly improving the privacy characteristics by construction.
Know What You Don't Know: Uncertainty Calibration of Process Reward Models
Jun 11, 2025Abstract:Process reward models (PRMs) play a central role in guiding inference-time scaling algorithms for large language models (LLMs). However, we observe that even state-of-the-art PRMs can be poorly calibrated and often overestimate success probabilities. To address this, we present a calibration approach, performed via quantile regression, that adjusts PRM outputs to better align with true success probabilities. Leveraging these calibrated success estimates and their associated confidence bounds, we introduce an \emph{instance-adaptive scaling} (IAS) framework that dynamically adjusts the inference budget based on the estimated likelihood that a partial reasoning trajectory will yield a correct final answer. Unlike conventional methods that allocate a fixed number of reasoning trajectories per query, this approach successfully adapts to each instance and reasoning step when using our calibrated PRMs. Experiments on mathematical reasoning benchmarks show that (i) our PRM calibration method successfully achieves small calibration error, outperforming the baseline methods, (ii) calibration is crucial for enabling effective adaptive scaling, and (iii) the proposed IAS strategy reduces inference costs while maintaining final answer accuracy, utilizing less compute on more confident problems as desired.
Revisiting Group Relative Policy Optimization: Insights into On-Policy and Off-Policy Training
May 28, 2025Abstract:We revisit Group Relative Policy Optimization (GRPO) in both on-policy and off-policy optimization regimes. Our motivation comes from recent work on off-policy Proximal Policy Optimization (PPO), which improves training stability, sampling efficiency, and memory usage. In addition, a recent analysis of GRPO suggests that estimating the advantage function with off-policy samples could be beneficial. Building on these observations, we adapt GRPO to the off-policy setting. We show that both on-policy and off-policy GRPO objectives yield an improvement in the reward. This result motivates the use of clipped surrogate objectives in the off-policy version of GRPO. We then compare the empirical performance of reinforcement learning with verifiable rewards in post-training using both GRPO variants. Our results show that off-policy GRPO either significantly outperforms or performs on par with its on-policy counterpart.
Activated LoRA: Fine-tuned LLMs for Intrinsics
Apr 16, 2025Abstract:Low-Rank Adaptation (LoRA) has emerged as a highly efficient framework for finetuning the weights of large foundation models, and has become the go-to method for data-driven customization of LLMs. Despite the promise of highly customized behaviors and capabilities, switching between relevant LoRAs in a multiturn setting is highly inefficient, as the key-value (KV) cache of the entire turn history must be recomputed with the LoRA weights before generation can begin. To address this problem, we propose Activated LoRA (aLoRA), which modifies the LoRA framework to only adapt weights for the tokens in the sequence \emph{after} the aLoRA is invoked. This change crucially allows aLoRA to accept the base model's KV cache of the input string, meaning that aLoRA can be instantly activated whenever needed in a chain without recomputing the cache. This enables building what we call \emph{intrinsics}, i.e. highly specialized models invoked to perform well-defined operations on portions of an input chain or conversation that otherwise uses the base model by default. We use aLoRA to train a set of intrinsics models, demonstrating competitive accuracy with standard LoRA while achieving significant inference benefits.
A Library of LLM Intrinsics for Retrieval-Augmented Generation
Apr 16, 2025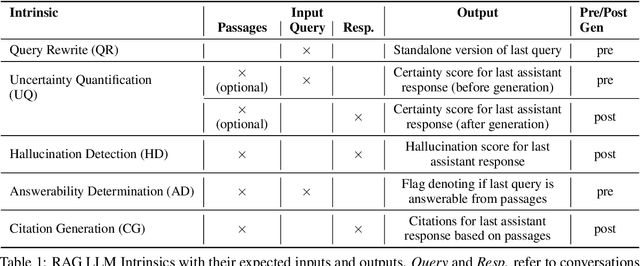
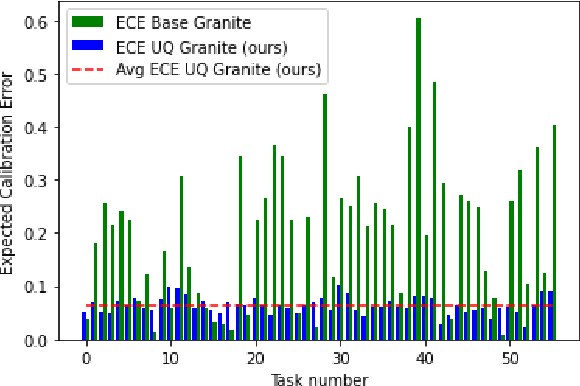

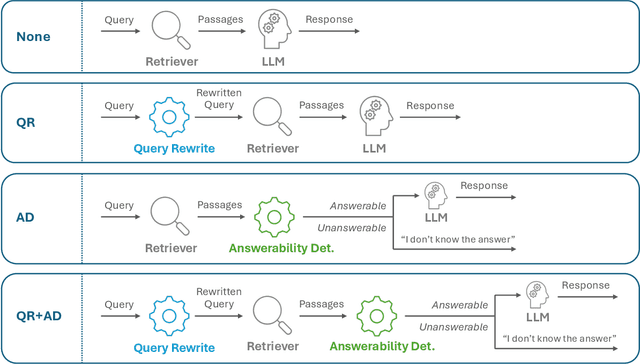
Abstract:In the developer community for large language models (LLMs), there is not yet a clean pattern analogous to a software library, to support very large scale collaboration. Even for the commonplace use case of Retrieval-Augmented Generation (RAG), it is not currently possible to write a RAG application against a well-defined set of APIs that are agreed upon by different LLM providers. Inspired by the idea of compiler intrinsics, we propose some elements of such a concept through introducing a library of LLM Intrinsics for RAG. An LLM intrinsic is defined as a capability that can be invoked through a well-defined API that is reasonably stable and independent of how the LLM intrinsic itself is implemented. The intrinsics in our library are released as LoRA adapters on HuggingFace, and through a software interface with clear structured input/output characteristics on top of vLLM as an inference platform, accompanied in both places with documentation and code. This article describes the intended usage, training details, and evaluations for each intrinsic, as well as compositions of multiple intrinsics.
Verify when Uncertain: Beyond Self-Consistency in Black Box Hallucination Detection
Feb 20, 2025Abstract:Large Language Models (LLMs) suffer from hallucination problems, which hinder their reliability in sensitive applications. In the black-box setting, several self-consistency-based techniques have been proposed for hallucination detection. We empirically study these techniques and show that they achieve performance close to that of a supervised (still black-box) oracle, suggesting little room for improvement within this paradigm. To address this limitation, we explore cross-model consistency checking between the target model and an additional verifier LLM. With this extra information, we observe improved oracle performance compared to purely self-consistency-based methods. We then propose a budget-friendly, two-stage detection algorithm that calls the verifier model only for a subset of cases. It dynamically switches between self-consistency and cross-consistency based on an uncertainty interval of the self-consistency classifier. We provide a geometric interpretation of consistency-based hallucination detection methods through the lens of kernel mean embeddings, offering deeper theoretical insights. Extensive experiments show that this approach maintains high detection performance while significantly reducing computational cost.
Privacy without Noisy Gradients: Slicing Mechanism for Generative Model Training
Oct 25, 2024



Abstract:Training generative models with differential privacy (DP) typically involves injecting noise into gradient updates or adapting the discriminator's training procedure. As a result, such approaches often struggle with hyper-parameter tuning and convergence. We consider the slicing privacy mechanism that injects noise into random low-dimensional projections of the private data, and provide strong privacy guarantees for it. These noisy projections are used for training generative models. To enable optimizing generative models using this DP approach, we introduce the smoothed-sliced $f$-divergence and show it enjoys statistical consistency. Moreover, we present a kernel-based estimator for this divergence, circumventing the need for adversarial training. Extensive numerical experiments demonstrate that our approach can generate synthetic data of higher quality compared with baselines. Beyond performance improvement, our method, by sidestepping the need for noisy gradients, offers data scientists the flexibility to adjust generator architecture and hyper-parameters, run the optimization over any number of epochs, and even restart the optimization process -- all without incurring additional privacy costs.
Domain Adaptable Prescriptive AI Agent for Enterprise
Jul 29, 2024



Abstract:Despite advancements in causal inference and prescriptive AI, its adoption in enterprise settings remains hindered primarily due to its technical complexity. Many users lack the necessary knowledge and appropriate tools to effectively leverage these technologies. This work at the MIT-IBM Watson AI Lab focuses on developing the proof-of-concept agent, PrecAIse, a domain-adaptable conversational agent equipped with a suite of causal and prescriptive tools to help enterprise users make better business decisions. The objective is to make advanced, novel causal inference and prescriptive tools widely accessible through natural language interactions. The presented Natural Language User Interface (NLUI) enables users with limited expertise in machine learning and data science to harness prescriptive analytics in their decision-making processes without requiring intensive computing resources. We present an agent capable of function calling, maintaining faithful, interactive, and dynamic conversations, and supporting new domains.
Gradient Flows and Riemannian Structure in the Gromov-Wasserstein Geometry
Jul 16, 2024



Abstract:The Wasserstein space of probability measures is known for its intricate Riemannian structure, which underpins the Wasserstein geometry and enables gradient flow algorithms. However, the Wasserstein geometry may not be suitable for certain tasks or data modalities. Motivated by scenarios where the global structure of the data needs to be preserved, this work initiates the study of gradient flows and Riemannian structure in the Gromov-Wasserstein (GW) geometry, which is particularly suited for such purposes. We focus on the inner product GW (IGW) distance between distributions on $\mathbb{R}^d$. Given a functional $\mathsf{F}:\mathcal{P}_2(\mathbb{R}^d)\to\mathbb{R}$ to optimize, we present an implicit IGW minimizing movement scheme that generates a sequence of distributions $\{\rho_i\}_{i=0}^n$, which are close in IGW and aligned in the 2-Wasserstein sense. Taking the time step to zero, we prove that the discrete solution converges to an IGW generalized minimizing movement (GMM) $(\rho_t)_t$ that follows the continuity equation with a velocity field $v_t\in L^2(\rho_t;\mathbb{R}^d)$, specified by a global transformation of the Wasserstein gradient of $\mathsf{F}$. The transformation is given by a mobility operator that modifies the Wasserstein gradient to encode not only local information, but also global structure. Our gradient flow analysis leads us to identify the Riemannian structure that gives rise to the intrinsic IGW geometry, using which we establish a Benamou-Brenier-like formula for IGW. We conclude with a formal derivation, akin to the Otto calculus, of the IGW gradient as the inverse mobility acting on the Wasserstein gradient. Numerical experiments validating our theory and demonstrating the global nature of IGW interpolations are provided.
Compress then Serve: Serving Thousands of LoRA Adapters with Little Overhead
Jun 17, 2024



Abstract:Fine-tuning large language models (LLMs) with low-rank adapters (LoRAs) has become common practice, often yielding numerous copies of the same LLM differing only in their LoRA updates. This paradigm presents challenges for systems that serve real-time responses to queries that each involve a different LoRA. Prior works optimize the design of such systems but still require continuous loading and offloading of LoRAs, as it is infeasible to store thousands of LoRAs in GPU memory. To mitigate this issue, we investigate the efficacy of compression when serving LoRA adapters. We consider compressing adapters individually via SVD and propose a method for joint compression of LoRAs into a shared basis paired with LoRA-specific scaling matrices. Our experiments with up to 500 LoRAs demonstrate that compressed LoRAs preserve performance while offering major throughput gains in realistic serving scenarios with over a thousand LoRAs, maintaining 75% of the throughput of serving a single LoRA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge