Gradient Flows and Riemannian Structure in the Gromov-Wasserstein Geometry

The Wasserstein space of probability measures is known for its intricate Riemannian structure, which underpins the Wasserstein geometry and enables gradient flow algorithms. However, the Wasserstein geometry may not be suitable for certain tasks or data modalities. Motivated by scenarios where the global structure of the data needs to be preserved, this work initiates the study of gradient flows and Riemannian structure in the Gromov-Wasserstein (GW) geometry, which is particularly suited for such purposes. We focus on the inner product GW (IGW) distance between distributions on $\mathbb{R}^d$. Given a functional $\mathsf{F}:\mathcal{P}_2(\mathbb{R}^d)\to\mathbb{R}$ to optimize, we present an implicit IGW minimizing movement scheme that generates a sequence of distributions $\{\rho_i\}_{i=0}^n$, which are close in IGW and aligned in the 2-Wasserstein sense. Taking the time step to zero, we prove that the discrete solution converges to an IGW generalized minimizing movement (GMM) $(\rho_t)_t$ that follows the continuity equation with a velocity field $v_t\in L^2(\rho_t;\mathbb{R}^d)$, specified by a global transformation of the Wasserstein gradient of $\mathsf{F}$. The transformation is given by a mobility operator that modifies the Wasserstein gradient to encode not only local information, but also global structure. Our gradient flow analysis leads us to identify the Riemannian structure that gives rise to the intrinsic IGW geometry, using which we establish a Benamou-Brenier-like formula for IGW. We conclude with a formal derivation, akin to the Otto calculus, of the IGW gradient as the inverse mobility acting on the Wasserstein gradient. Numerical experiments validating our theory and demonstrating the global nature of IGW interpolations are provided.

Nyström Kernel Stein Discrepancy

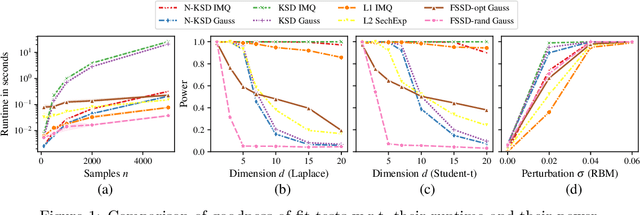
Kernel methods underpin many of the most successful approaches in data science and statistics, and they allow representing probability measures as elements of a reproducing kernel Hilbert space without loss of information. Recently, the kernel Stein discrepancy (KSD), which combines Stein's method with kernel techniques, gained considerable attention. Through the Stein operator, KSD allows the construction of powerful goodness-of-fit tests where it is sufficient to know the target distribution up to a multiplicative constant. However, the typical U- and V-statistic-based KSD estimators suffer from a quadratic runtime complexity, which hinders their application in large-scale settings. In this work, we propose a Nystr\"om-based KSD acceleration -- with runtime $\mathcal O\!\left(mn+m^3\right)$ for $n$ samples and $m\ll n$ Nystr\"om points -- , show its $\sqrt{n}$-consistency under the null with a classical sub-Gaussian assumption, and demonstrate its applicability for goodness-of-fit testing on a suite of benchmarks.

Spectral Regularized Kernel Goodness-of-Fit Tests

Maximum mean discrepancy (MMD) has enjoyed a lot of success in many machine learning and statistical applications, including non-parametric hypothesis testing, because of its ability to handle non-Euclidean data. Recently, it has been demonstrated in Balasubramanian et al.(2021) that the goodness-of-fit test based on MMD is not minimax optimal while a Tikhonov regularized version of it is, for an appropriate choice of the regularization parameter. However, the results in Balasubramanian et al. (2021) are obtained under the restrictive assumptions of the mean element being zero, and the uniform boundedness condition on the eigenfunctions of the integral operator. Moreover, the test proposed in Balasubramanian et al. (2021) is not practical as it is not computable for many kernels. In this paper, we address these shortcomings and extend the results to general spectral regularizers that include Tikhonov regularization.

Kernel $ε$-Greedy for Contextual Bandits

We consider a kernelized version of the $\epsilon$-greedy strategy for contextual bandits. More precisely, in a setting with finitely many arms, we consider that the mean reward functions lie in a reproducing kernel Hilbert space (RKHS). We propose an online weighted kernel ridge regression estimator for the reward functions. Under some conditions on the exploration probability sequence, $\{\epsilon_t\}_t$, and choice of the regularization parameter, $\{\lambda_t\}_t$, we show that the proposed estimator is consistent. We also show that for any choice of kernel and the corresponding RKHS, we achieve a sub-linear regret rate depending on the intrinsic dimensionality of the RKHS. Furthermore, we achieve the optimal regret rate of $\sqrt{T}$ under a margin condition for finite-dimensional RKHS.

Spectral Regularized Kernel Two-Sample Tests

Over the last decade, an approach that has gained a lot of popularity to tackle non-parametric testing problems on general (i.e., non-Euclidean) domains is based on the notion of reproducing kernel Hilbert space (RKHS) embedding of probability distributions. The main goal of our work is to understand the optimality of two-sample tests constructed based on this approach. First, we show that the popular MMD (maximum mean discrepancy) two-sample test is not optimal in terms of the separation boundary measured in Hellinger distance. Second, we propose a modification to the MMD test based on spectral regularization by taking into account the covariance information (which is not captured by the MMD test) and prove the proposed test to be minimax optimal with a smaller separation boundary than that achieved by the MMD test. Third, we propose an adaptive version of the above test which involves a data-driven strategy to choose the regularization parameter and show the adaptive test to be almost minimax optimal up to a logarithmic factor. Moreover, our results hold for the permutation variant of the test where the test threshold is chosen elegantly through the permutation of the samples. Through numerical experiments on synthetic and real-world data, we demonstrate the superior performance of the proposed test in comparison to the MMD test.

Regularized Stein Variational Gradient Flow

The Stein Variational Gradient Descent (SVGD) algorithm is an deterministic particle method for sampling. However, a mean-field analysis reveals that the gradient flow corresponding to the SVGD algorithm (i.e., the Stein Variational Gradient Flow) only provides a constant-order approximation to the Wasserstein Gradient Flow corresponding to the KL-divergence minimization. In this work, we propose the Regularized Stein Variational Gradient Flow which interpolates between the Stein Variational Gradient Flow and the Wasserstein Gradient Flow. We establish various theoretical properties of the Regularized Stein Variational Gradient Flow (and its time-discretization) including convergence to equilibrium, existence and uniqueness of weak solutions, and stability of the solutions. We provide preliminary numerical evidence of the improved performance offered by the regularization.

Shrinkage Estimation of Higher Order Bochner Integrals

We consider shrinkage estimation of higher order Hilbert space valued Bochner integrals in a non-parametric setting. We propose estimators that shrink the $U$-statistic estimator of the Bochner integral towards a pre-specified target element in the Hilbert space. Depending on the degeneracy of the kernel of the $U$-statistic, we construct consistent shrinkage estimators with fast rates of convergence, and develop oracle inequalities comparing the risks of the the $U$-statistic estimator and its shrinkage version. Surprisingly, we show that the shrinkage estimator designed by assuming complete degeneracy of the kernel of the $U$-statistic is a consistent estimator even when the kernel is not complete degenerate. This work subsumes and improves upon Krikamol et al., 2016, JMLR and Zhou et al., 2019, JMVA, which only handle mean element and covariance operator estimation in a reproducing kernel Hilbert space. We also specialize our results to normal mean estimation and show that for $d\ge 3$, the proposed estimator strictly improves upon the sample mean in terms of the mean squared error.

Robust Topological Inference in the Presence of Outliers

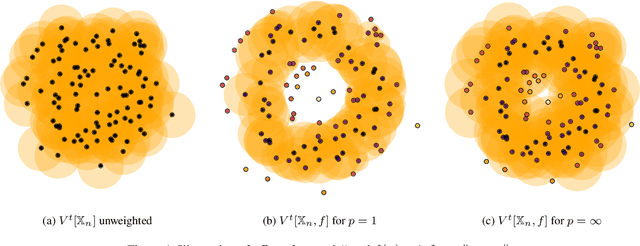
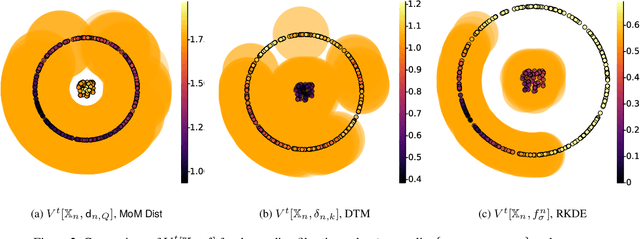
The distance function to a compact set plays a crucial role in the paradigm of topological data analysis. In particular, the sublevel sets of the distance function are used in the computation of persistent homology -- a backbone of the topological data analysis pipeline. Despite its stability to perturbations in the Hausdorff distance, persistent homology is highly sensitive to outliers. In this work, we develop a framework of statistical inference for persistent homology in the presence of outliers. Drawing inspiration from recent developments in robust statistics, we propose a $\textit{median-of-means}$ variant of the distance function ($\textsf{MoM Dist}$), and establish its statistical properties. In particular, we show that, even in the presence of outliers, the sublevel filtrations and weighted filtrations induced by $\textsf{MoM Dist}$ are both consistent estimators of the true underlying population counterpart, and their rates of convergence in the bottleneck metric are controlled by the fraction of outliers in the data. Finally, we demonstrate the advantages of the proposed methodology through simulations and applications.

Cycle Consistent Probability Divergences Across Different Spaces

Discrepancy measures between probability distributions are at the core of statistical inference and machine learning. In many applications, distributions of interest are supported on different spaces, and yet a meaningful correspondence between data points is desired. Motivated to explicitly encode consistent bidirectional maps into the discrepancy measure, this work proposes a novel unbalanced Monge optimal transport formulation for matching, up to isometries, distributions on different spaces. Our formulation arises as a principled relaxation of the Gromov-Haussdroff distance between metric spaces, and employs two cycle-consistent maps that push forward each distribution onto the other. We study structural properties of the proposed discrepancy and, in particular, show that it captures the popular cycle-consistent generative adversarial network (GAN) framework as a special case, thereby providing the theory to explain it. Motivated by computational efficiency, we then kernelize the discrepancy and restrict the mappings to parametric function classes. The resulting kernelized version is coined the generalized maximum mean discrepancy (GMMD). Convergence rates for empirical estimation of GMMD are studied and experiments to support our theory are provided.

On Distance and Kernel Measures of Conditional Independence

Measuring conditional independence is one of the important tasks in statistical inference and is fundamental in causal discovery, feature selection, dimensionality reduction, Bayesian network learning, and others. In this work, we explore the connection between conditional independence measures induced by distances on a metric space and reproducing kernels associated with a reproducing kernel Hilbert space (RKHS). For certain distance and kernel pairs, we show the distance-based conditional independence measures to be equivalent to that of kernel-based measures. On the other hand, we also show that some popular---in machine learning---kernel conditional independence measures based on the Hilbert-Schmidt norm of a certain cross-conditional covariance operator, do not have a simple distance representation, except in some limiting cases. This paper, therefore, shows the distance and kernel measures of conditional independence to be not quite equivalent unlike in the case of joint independence as shown by Sejdinovic et al. (2013).