To Switch or Not to Switch? Balanced Policy Switching in Offline Reinforcement Learning

Reinforcement learning (RL) -- finding the optimal behaviour (also referred to as policy) maximizing the collected long-term cumulative reward -- is among the most influential approaches in machine learning with a large number of successful applications. In several decision problems, however, one faces the possibility of policy switching -- changing from the current policy to a new one -- which incurs a non-negligible cost (examples include the shifting of the currently applied educational technology, modernization of a computing cluster, and the introduction of a new webpage design), and in the decision one is limited to using historical data without the availability for further online interaction. Despite the inevitable importance of this offline learning scenario, to our best knowledge, very little effort has been made to tackle the key problem of balancing between the gain and the cost of switching in a flexible and principled way. Leveraging ideas from the area of optimal transport, we initialize the systematic study of policy switching in offline RL. We establish fundamental properties and design a Net Actor-Critic algorithm for the proposed novel switching formulation. Numerical experiments demonstrate the efficiency of our approach on multiple benchmarks of the Gymnasium.

Forward and Backward State Abstractions for Off-policy Evaluation

Off-policy evaluation (OPE) is crucial for evaluating a target policy's impact offline before its deployment. However, achieving accurate OPE in large state spaces remains challenging.This paper studies state abstractions-originally designed for policy learning-in the context of OPE. Our contributions are three-fold: (i) We define a set of irrelevance conditions central to learning state abstractions for OPE. (ii) We derive sufficient conditions for achieving irrelevance in Q-functions and marginalized importance sampling ratios, the latter obtained by constructing a time-reversed Markov decision process (MDP) based on the observed MDP. (iii) We propose a novel two-step procedure that sequentially projects the original state space into a smaller space, which substantially simplify the sample complexity of OPE arising from high cardinality.

Nyström Kernel Stein Discrepancy

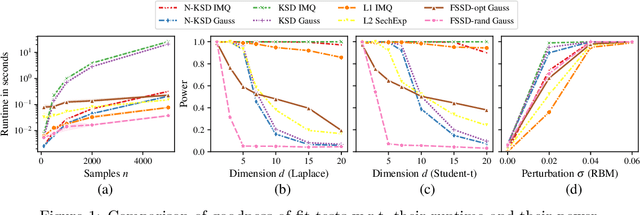
Kernel methods underpin many of the most successful approaches in data science and statistics, and they allow representing probability measures as elements of a reproducing kernel Hilbert space without loss of information. Recently, the kernel Stein discrepancy (KSD), which combines Stein's method with kernel techniques, gained considerable attention. Through the Stein operator, KSD allows the construction of powerful goodness-of-fit tests where it is sufficient to know the target distribution up to a multiplicative constant. However, the typical U- and V-statistic-based KSD estimators suffer from a quadratic runtime complexity, which hinders their application in large-scale settings. In this work, we propose a Nystr\"om-based KSD acceleration -- with runtime $\mathcal O\!\left(mn+m^3\right)$ for $n$ samples and $m\ll n$ Nystr\"om points -- , show its $\sqrt{n}$-consistency under the null with a classical sub-Gaussian assumption, and demonstrate its applicability for goodness-of-fit testing on a suite of benchmarks.

The Minimax Rate of HSIC Estimation for Translation-Invariant Kernels

Kernel techniques are among the most influential approaches in data science and statistics. Under mild conditions, the reproducing kernel Hilbert space associated to a kernel is capable of encoding the independence of $M\ge 2$ random variables. Probably the most widespread independence measure relying on kernels is the so-called Hilbert-Schmidt independence criterion (HSIC; also referred to as distance covariance in the statistics literature). Despite various existing HSIC estimators designed since its introduction close to two decades ago, the fundamental question of the rate at which HSIC can be estimated is still open. In this work, we prove that the minimax optimal rate of HSIC estimation on $\mathbb R^d$ for Borel measures containing the Gaussians with continuous bounded translation-invariant characteristic kernels is $\mathcal O\!\left(n^{-1/2}\right)$. Specifically, our result implies the optimality in the minimax sense of many of the most-frequently used estimators (including the U-statistic, the V-statistic, and the Nystr\"om-based one) on $\mathbb R^d$.

Random Fourier Signature Features

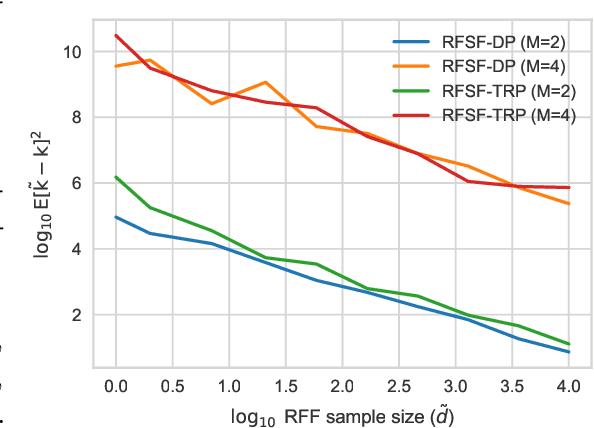
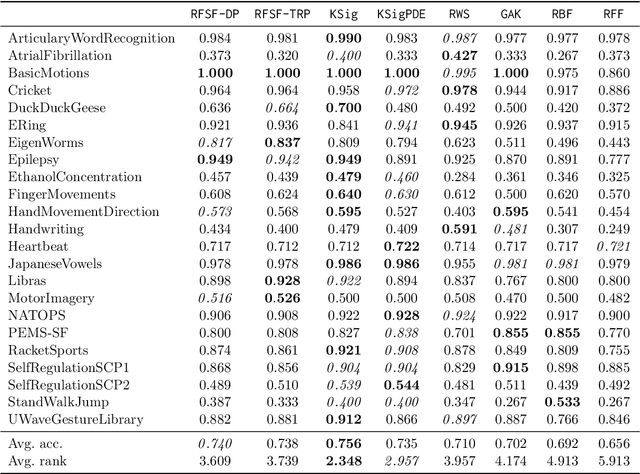
Tensor algebras give rise to one of the most powerful measures of similarity for sequences of arbitrary length called the signature kernel accompanied with attractive theoretical guarantees from stochastic analysis. Previous algorithms to compute the signature kernel scale quadratically in terms of the length and the number of the sequences. To mitigate this severe computational bottleneck, we develop a random Fourier feature-based acceleration of the signature kernel acting on the inherently non-Euclidean domain of sequences. We show uniform approximation guarantees for the proposed unbiased estimator of the signature kernel, while keeping its computation linear in the sequence length and number. In addition, combined with recent advances on tensor projections, we derive two even more scalable time series features with favourable concentration properties and computational complexity both in time and memory. Our empirical results show that the reduction in computational cost comes at a negligible price in terms of accuracy on moderate-sized datasets, and it enables one to scale to large datasets up to a million time series.

Functional Output Regression with Infimal Convolution: Exploring the Huber and $ε$-insensitive Losses

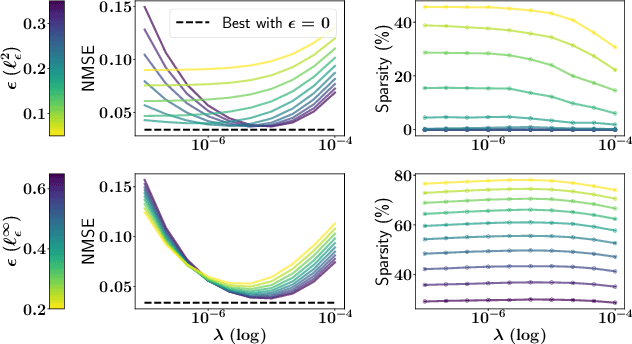
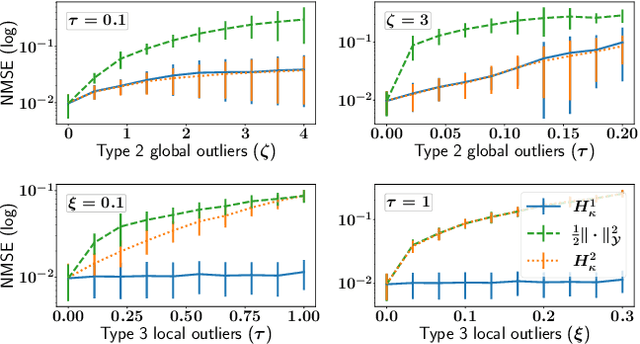
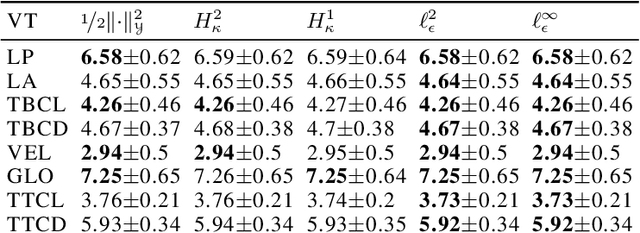
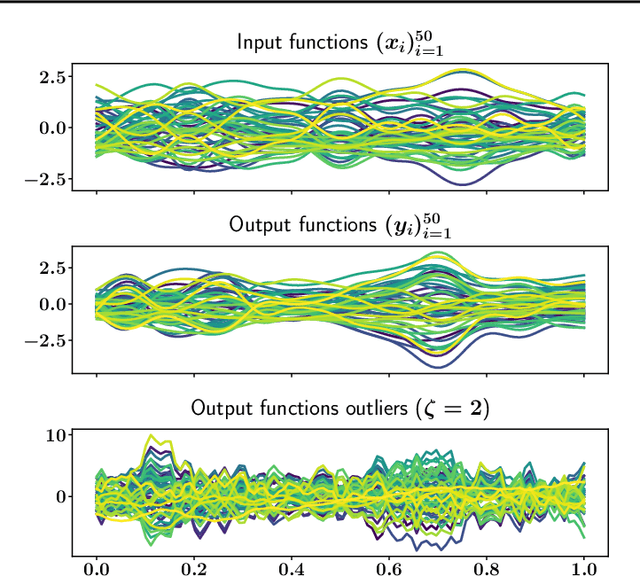
The focus of the paper is functional output regression (FOR) with convoluted losses. While most existing work consider the square loss setting, we leverage extensions of the Huber and the $\epsilon$-insensitive loss (induced by infimal convolution) and propose a flexible framework capable of handling various forms of outliers and sparsity in the FOR family. We derive computationally tractable algorithms relying on duality to tackle the resulting tasks in the context of vector-valued reproducing kernel Hilbert spaces. The efficiency of the approach is demonstrated and contrasted with the classical squared loss setting on both synthetic and real-world benchmarks.

Handling Hard Affine SDP Shape Constraints in RKHSs

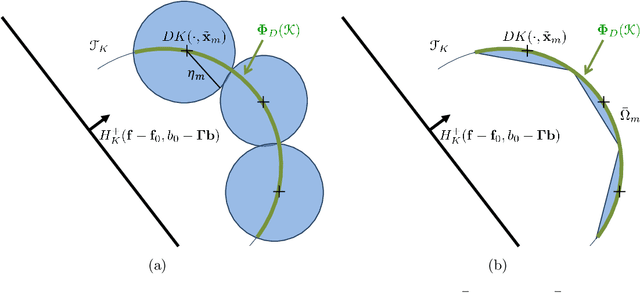
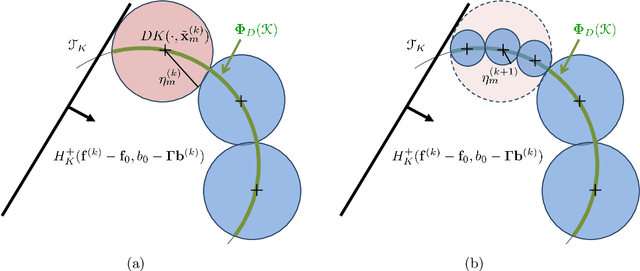
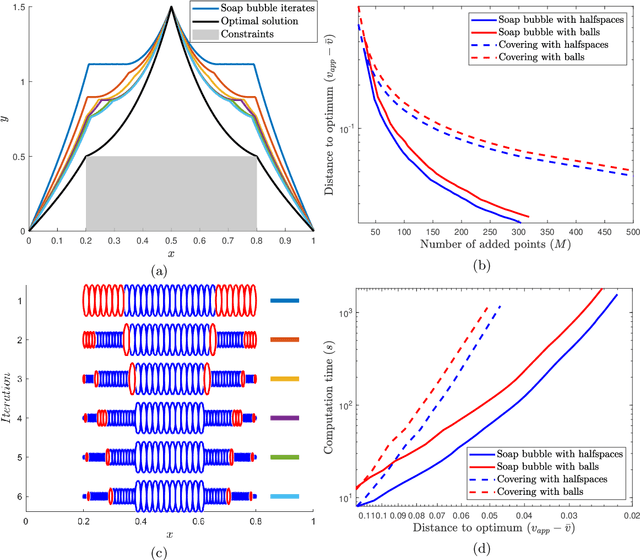
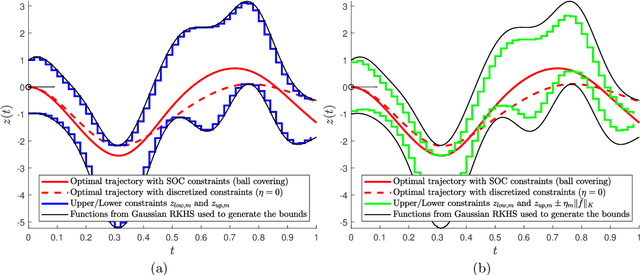
Shape constraints, such as non-negativity, monotonicity, convexity or supermodularity, play a key role in various applications of machine learning and statistics. However, incorporating this side information into predictive models in a hard way (for example at all points of an interval) for rich function classes is a notoriously challenging problem. We propose a unified and modular convex optimization framework, relying on second-order cone (SOC) tightening, to encode hard affine SDP constraints on function derivatives, for models belonging to vector-valued reproducing kernel Hilbert spaces (vRKHSs). The modular nature of the proposed approach allows to simultaneously handle multiple shape constraints, and to tighten an infinite number of constraints into finitely many. We prove the consistency of the proposed scheme and that of its adaptive variant, leveraging geometric properties of vRKHSs. The efficiency of the approach is illustrated in the context of shape optimization, safety-critical control and econometrics.

Hard Shape-Constrained Kernel Machines

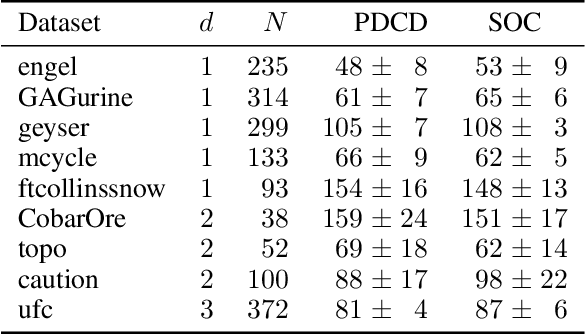
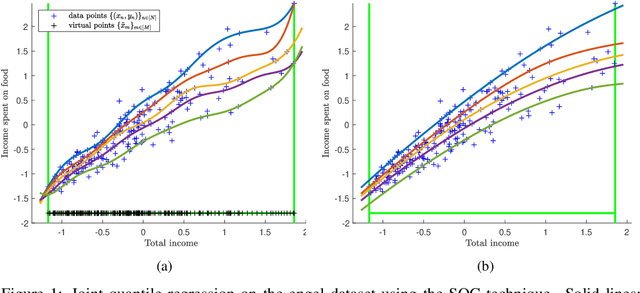
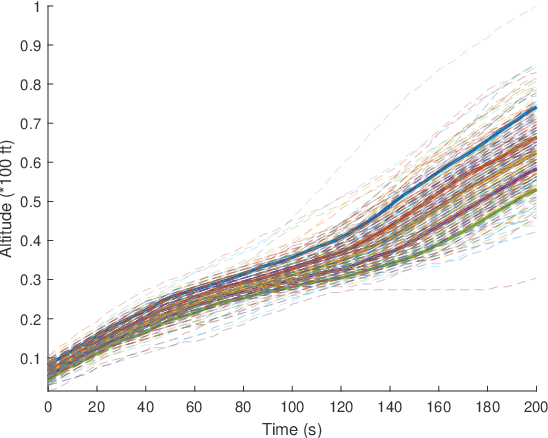
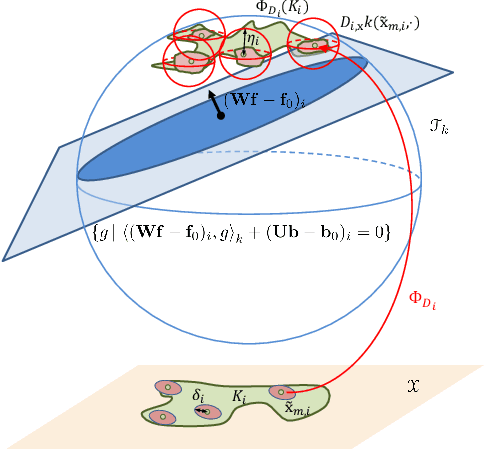
Shape constraints (such as non-negativity, monotonicity, convexity) play a central role in a large number of applications, as they usually improve performance for small sample size and help interpretability. However enforcing these shape requirements in a hard fashion is an extremely challenging problem. Classically, this task is tackled (i) in a soft way (without out-of-sample guarantees), (ii) by specialized transformation of the variables on a case-by-case basis, or (iii) by using highly restricted function classes, such as polynomials or polynomial splines. In this paper, we prove that hard affine shape constraints on function derivatives can be encoded in kernel machines which represent one of the most flexible and powerful tools in machine learning and statistics. Particularly, we present a tightened second-order cone constrained reformulation, that can be readily implemented in convex solvers. We prove performance guarantees on the solution, and demonstrate the efficiency of the approach in joint quantile regression with applications to economics and to the analysis of aircraft trajectories, among others.

On Kernel Derivative Approximation with Random Fourier Features

Random Fourier features (RFF) represent one of the most popular and wide-spread techniques in machine learning to scale up kernel algorithms. Despite the numerous successful applications of RFFs, unfortunately, quite little is understood theoretically on their optimality and limitations of their performance. To the best of our knowledge, the only existing areas where precise statistical-computational trade-offs have been established are approximation of kernel values, kernel ridge regression, and kernel principal component analysis. Our goal is to spark the investigation of optimality of RFF-based approximations in tasks involving not only function values but derivatives, which naturally lead to optimization problems with kernel derivatives. Particularly, in this paper, we focus on the approximation quality of RFFs for kernel derivatives and prove that the existing finite-sample guarantees can be improved exponentially in terms of the domain where they hold, using recent tools from unbounded empirical process theory. Our result implies that the same approximation guarantee is achievable for kernel derivatives using RFF as for kernel values.

MONK -- Outlier-Robust Mean Embedding Estimation by Median-of-Means

Mean embeddings provide an extremely flexible and powerful tool in machine learning and statistics to represent probability distributions and define a semi-metric (MMD, maximum mean discrepancy; also called N-distance or energy distance), with numerous successful applications. The representation is constructed as the expectation of the feature map defined by a kernel. As a mean, its classical empirical estimator, however, can be arbitrary severely affected even by a single outlier in case of unbounded features. To the best of our knowledge, unfortunately even the consistency of the existing few techniques trying to alleviate this serious sensitivity bottleneck is unknown. In this paper, we show how the recently emerged principle of median-of-means can be used to design estimators for kernel mean embedding and MMD with excessive resistance properties to outliers, and optimal sub-Gaussian deviation bounds under mild assumptions.