Learning in Feature Spaces via Coupled Covariances: Asymmetric Kernel SVD and Nyström method

In contrast with Mercer kernel-based approaches as used e.g., in Kernel Principal Component Analysis (KPCA), it was previously shown that Singular Value Decomposition (SVD) inherently relates to asymmetric kernels and Asymmetric Kernel Singular Value Decomposition (KSVD) has been proposed. However, the existing formulation to KSVD cannot work with infinite-dimensional feature mappings, the variational objective can be unbounded, and needs further numerical evaluation and exploration towards machine learning. In this work, i) we introduce a new asymmetric learning paradigm based on coupled covariance eigenproblem (CCE) through covariance operators, allowing infinite-dimensional feature maps. The solution to CCE is ultimately obtained from the SVD of the induced asymmetric kernel matrix, providing links to KSVD. ii) Starting from the integral equations corresponding to a pair of coupled adjoint eigenfunctions, we formalize the asymmetric Nystr\"om method through a finite sample approximation to speed up training. iii) We provide the first empirical evaluations verifying the practical utility and benefits of KSVD and compare with methods resorting to symmetrization or linear SVD across multiple tasks.

Extending Kernel PCA through Dualization: Sparsity, Robustness and Fast Algorithms

The goal of this paper is to revisit Kernel Principal Component Analysis (KPCA) through dualization of a difference of convex functions. This allows to naturally extend KPCA to multiple objective functions and leads to efficient gradient-based algorithms avoiding the expensive SVD of the Gram matrix. Particularly, we consider objective functions that can be written as Moreau envelopes, demonstrating how to promote robustness and sparsity within the same framework. The proposed method is evaluated on synthetic and real-world benchmarks, showing significant speedup in KPCA training time as well as highlighting the benefits in terms of robustness and sparsity.

Functional Output Regression with Infimal Convolution: Exploring the Huber and $ε$-insensitive Losses

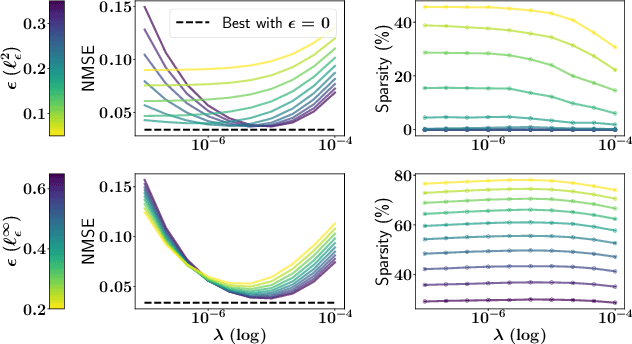
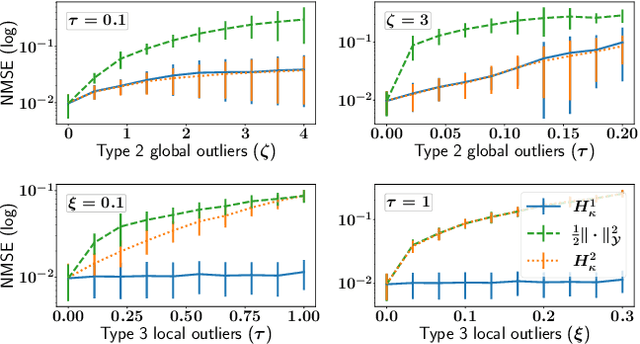
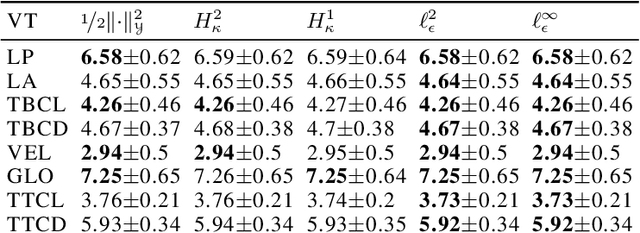
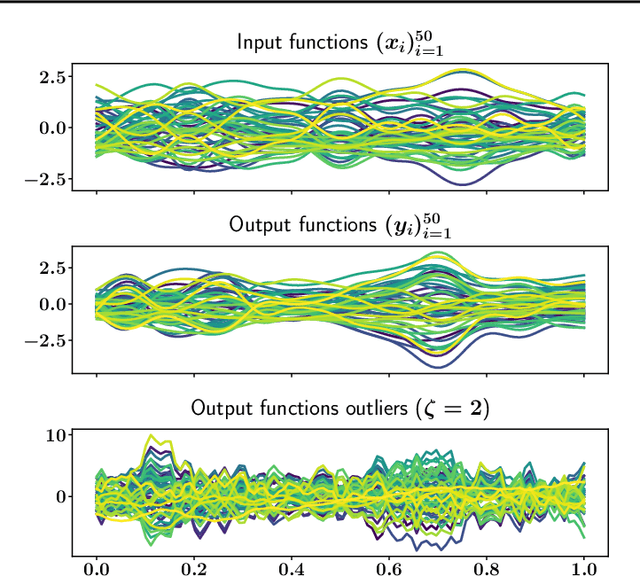
The focus of the paper is functional output regression (FOR) with convoluted losses. While most existing work consider the square loss setting, we leverage extensions of the Huber and the $\epsilon$-insensitive loss (induced by infimal convolution) and propose a flexible framework capable of handling various forms of outliers and sparsity in the FOR family. We derive computationally tractable algorithms relying on duality to tackle the resulting tasks in the context of vector-valued reproducing kernel Hilbert spaces. The efficiency of the approach is demonstrated and contrasted with the classical squared loss setting on both synthetic and real-world benchmarks.

Emotion Transfer Using Vector-Valued Infinite Task Learning

Style transfer is a significant problem of machine learning with numerous successful applications. In this work, we present a novel style transfer framework building upon infinite task learning and vector-valued reproducing kernel Hilbert spaces. We instantiate the idea in emotion transfer where the goal is to transform facial images to different target emotions. The proposed approach provides a principled way to gain explicit control over the continuous style space. We demonstrate the efficiency of the technique on popular facial emotion benchmarks, achieving low reconstruction cost and high emotion classification accuracy.

On the Dualization of Operator-Valued Kernel Machines

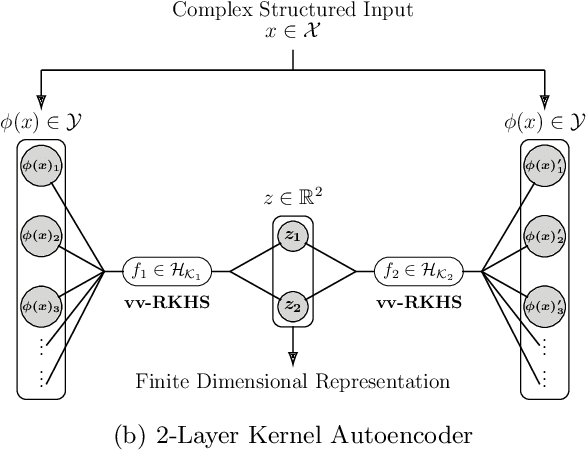
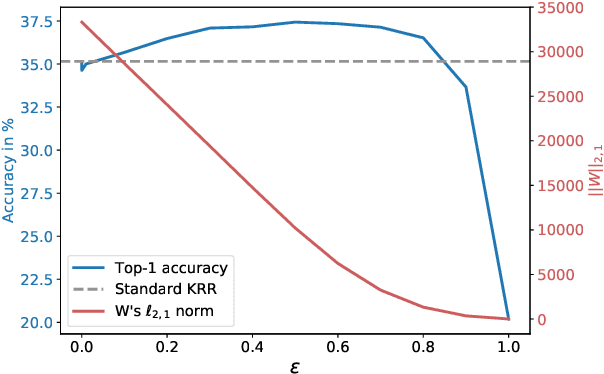
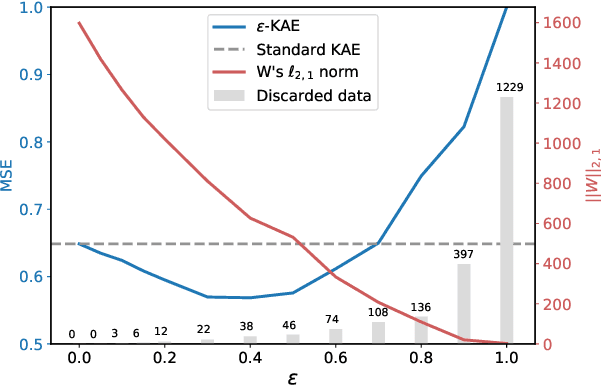
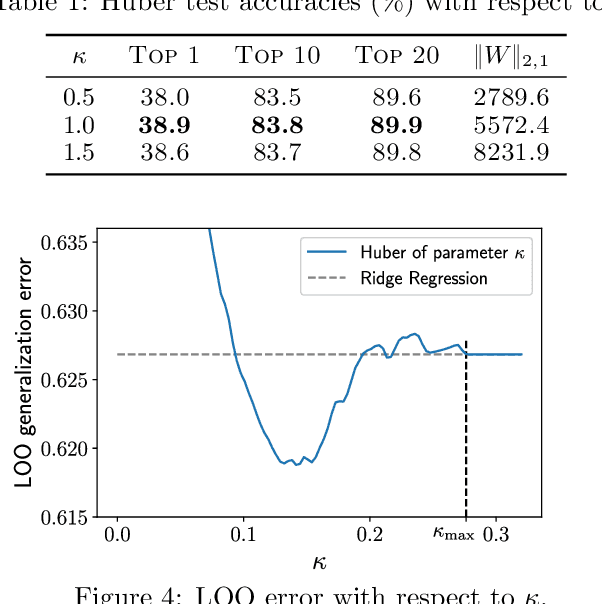
Operator-Valued Kernels (OVKs) and Vector-Valued Reproducing Kernel Hilbert Spaces (vv-RKHSs) provide an elegant way to extend scalar kernel methods when the output space is a Hilbert space. First used in multi-task regression, this theoretical framework opens the door to various applications, ranging from structured output prediction to functional regression, thanks to its ability to deal with infinite dimensional output spaces. This work investigates how to use the duality principle to handle different families of loss functions, yet unexplored within vv-RKHSs. The difficulty of having infinite dimensional dual variables is overcome, either by means of a Double Representer Theorem when the loss depends on inner products solely, or by an in-depth analysis of the Fenchel-Legendre transform of integral losses. Experiments on structured prediction, function-to-function regression and structured representation learning with $\epsilon$-insensitive and Huber losses illustrate the benefits of this framework.

Infinite-Task Learning with RKHSs

Machine learning has witnessed tremendous success in solving tasks depending on a single hyperparameter. When considering simultaneously a finite number of tasks, multi-task learning enables one to account for the similarities of the tasks via appropriate regularizers. A step further consists of learning a continuum of tasks for various loss functions. A promising approach, called \emph{Parametric Task Learning}, has paved the way in the continuum setting for affine models and piecewise-linear loss functions. In this work, we introduce a novel approach called \emph{Infinite Task Learning} whose goal is to learn a function whose output is a function over the hyperparameter space. We leverage tools from operator-valued kernels and the associated vector-valued RKHSs that provide an explicit control over the role of the hyperparameters, and also allows us to consider new type of constraints. We provide generalization guarantees to the suggested scheme and illustrate its efficiency in cost-sensitive classification, quantile regression and density level set estimation.