Infinite-Task Learning with RKHSs

Machine learning has witnessed tremendous success in solving tasks depending on a single hyperparameter. When considering simultaneously a finite number of tasks, multi-task learning enables one to account for the similarities of the tasks via appropriate regularizers. A step further consists of learning a continuum of tasks for various loss functions. A promising approach, called \emph{Parametric Task Learning}, has paved the way in the continuum setting for affine models and piecewise-linear loss functions. In this work, we introduce a novel approach called \emph{Infinite Task Learning} whose goal is to learn a function whose output is a function over the hyperparameter space. We leverage tools from operator-valued kernels and the associated vector-valued RKHSs that provide an explicit control over the role of the hyperparameters, and also allows us to consider new type of constraints. We provide generalization guarantees to the suggested scheme and illustrate its efficiency in cost-sensitive classification, quantile regression and density level set estimation.

One Class Splitting Criteria for Random Forests

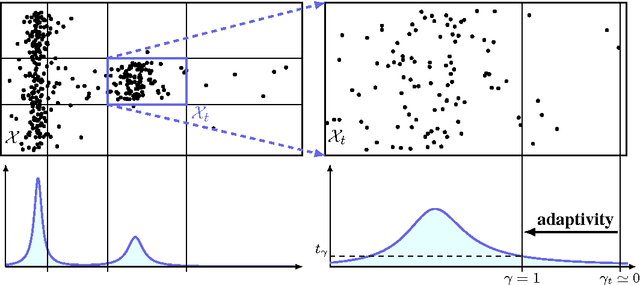
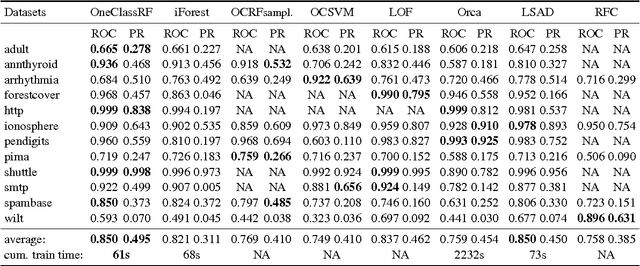
Random Forests (RFs) are strong machine learning tools for classification and regression. However, they remain supervised algorithms, and no extension of RFs to the one-class setting has been proposed, except for techniques based on second-class sampling. This work fills this gap by proposing a natural methodology to extend standard splitting criteria to the one-class setting, structurally generalizing RFs to one-class classification. An extensive benchmark of seven state-of-the-art anomaly detection algorithms is also presented. This empirically demonstrates the relevance of our approach.

Random Fourier Features for Operator-Valued Kernels

Devoted to multi-task learning and structured output learning, operator-valued kernels provide a flexible tool to build vector-valued functions in the context of Reproducing Kernel Hilbert Spaces. To scale up these methods, we extend the celebrated Random Fourier Feature methodology to get an approximation of operator-valued kernels. We propose a general principle for Operator-valued Random Fourier Feature construction relying on a generalization of Bochner's theorem for translation-invariant operator-valued Mercer kernels. We prove the uniform convergence of the kernel approximation for bounded and unbounded operator random Fourier features using appropriate Bernstein matrix concentration inequality. An experimental proof-of-concept shows the quality of the approximation and the efficiency of the corresponding linear models on example datasets.