Nyström $M$-Hilbert-Schmidt Independence Criterion

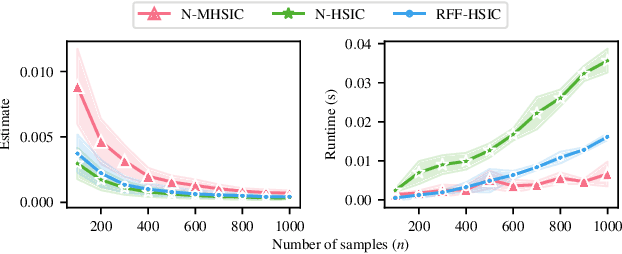
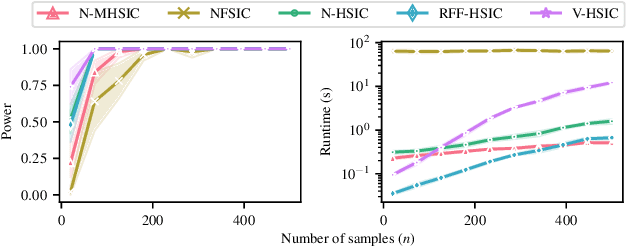
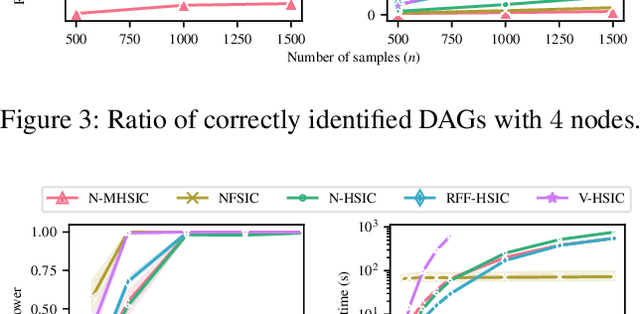
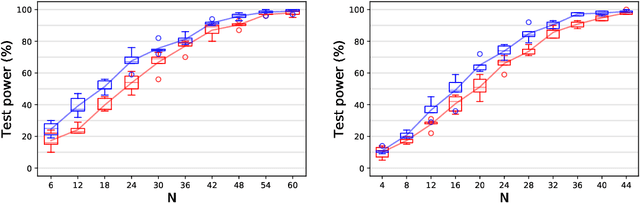
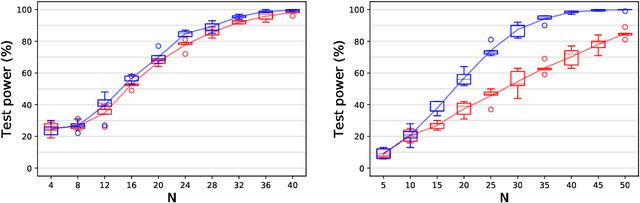
Kernel techniques are among the most popular and powerful approaches of data science. Among the key features that make kernels ubiquitous are (i) the number of domains they have been designed for, (ii) the Hilbert structure of the function class associated to kernels facilitating their statistical analysis, and (iii) their ability to represent probability distributions without loss of information. These properties give rise to the immense success of Hilbert-Schmidt independence criterion (HSIC) which is able to capture joint independence of random variables under mild conditions, and permits closed-form estimators with quadratic computational complexity (w.r.t. the sample size). In order to alleviate the quadratic computational bottleneck in large-scale applications, multiple HSIC approximations have been proposed, however these estimators are restricted to $M=2$ random variables, do not extend naturally to the $M\ge 2$ case, and lack theoretical guarantees. In this work, we propose an alternative Nystr\"om-based HSIC estimator which handles the $M\ge 2$ case, prove its consistency, and demonstrate its applicability in multiple contexts, including synthetic examples, dependency testing of media annotations, and causal discovery.

Kernelized Cumulants: Beyond Kernel Mean Embeddings

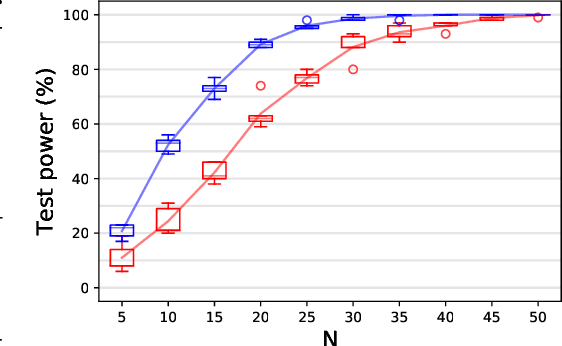
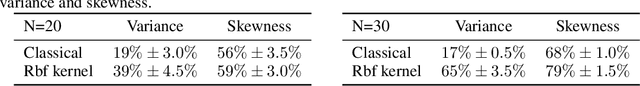
In $\mathbb R^d$, it is well-known that cumulants provide an alternative to moments that can achieve the same goals with numerous benefits such as lower variance estimators. In this paper we extend cumulants to reproducing kernel Hilbert spaces (RKHS) using tools from tensor algebras and show that they are computationally tractable by a kernel trick. These kernelized cumulants provide a new set of all-purpose statistics; the classical maximum mean discrepancy and Hilbert-Schmidt independence criterion arise as the degree one objects in our general construction. We argue both theoretically and empirically (on synthetic, environmental, and traffic data analysis) that going beyond degree one has several advantages and can be achieved with the same computational complexity and minimal overhead in our experiments.

Discussion of `Multiscale Fisher's Independence Test for Multivariate Dependence'

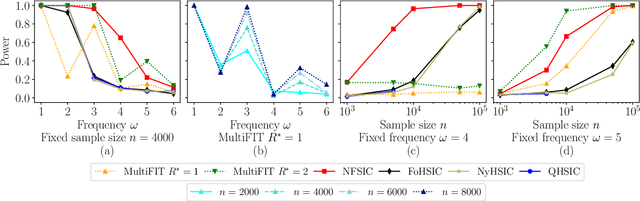
We discuss how MultiFIT, the Multiscale Fisher's Independence Test for Multivariate Dependence proposed by Gorsky and Ma (2022), compares to existing linear-time kernel tests based on the Hilbert-Schmidt independence criterion (HSIC). We highlight the fact that the levels of the kernel tests at any finite sample size can be controlled exactly, as it is the case with the level of MultiFIT. In our experiments, we observe some of the performance limitations of MultiFIT in terms of test power.

Kernel Minimum Divergence Portfolios

Portfolio optimization is a key challenge in finance with the aim of creating portfolios matching the investors' preference. The target distribution approach relying on the Kullback-Leibler or the $f$-divergence represents one of the most effective forms of achieving this goal. In this paper, we propose to use kernel and optimal transport (KOT) based divergences to tackle the task, which relax the assumptions and the optimization constraints of the previous approaches. In case of the kernel-based maximum mean discrepancy (MMD) we (i) prove the analytic computability of the underlying mean embedding for various target distribution-kernel pairs, (ii) show that such analytic knowledge can lead to faster convergence of MMD estimators, and (iii) extend the results to the unbounded exponential kernel with minimax lower bounds. Numerical experiments demonstrate the improved performance of our KOT estimators both on synthetic and real-world examples.

Emotion Transfer Using Vector-Valued Infinite Task Learning

Style transfer is a significant problem of machine learning with numerous successful applications. In this work, we present a novel style transfer framework building upon infinite task learning and vector-valued reproducing kernel Hilbert spaces. We instantiate the idea in emotion transfer where the goal is to transform facial images to different target emotions. The proposed approach provides a principled way to gain explicit control over the continuous style space. We demonstrate the efficiency of the technique on popular facial emotion benchmarks, achieving low reconstruction cost and high emotion classification accuracy.

Infinite-Task Learning with RKHSs

Machine learning has witnessed tremendous success in solving tasks depending on a single hyperparameter. When considering simultaneously a finite number of tasks, multi-task learning enables one to account for the similarities of the tasks via appropriate regularizers. A step further consists of learning a continuum of tasks for various loss functions. A promising approach, called \emph{Parametric Task Learning}, has paved the way in the continuum setting for affine models and piecewise-linear loss functions. In this work, we introduce a novel approach called \emph{Infinite Task Learning} whose goal is to learn a function whose output is a function over the hyperparameter space. We leverage tools from operator-valued kernels and the associated vector-valued RKHSs that provide an explicit control over the role of the hyperparameters, and also allows us to consider new type of constraints. We provide generalization guarantees to the suggested scheme and illustrate its efficiency in cost-sensitive classification, quantile regression and density level set estimation.

Kernel-Based Just-In-Time Learning for Passing Expectation Propagation Messages

We propose an efficient nonparametric strategy for learning a message operator in expectation propagation (EP), which takes as input the set of incoming messages to a factor node, and produces an outgoing message as output. This learned operator replaces the multivariate integral required in classical EP, which may not have an analytic expression. We use kernel-based regression, which is trained on a set of probability distributions representing the incoming messages, and the associated outgoing messages. The kernel approach has two main advantages: first, it is fast, as it is implemented using a novel two-layer random feature representation of the input message distributions; second, it has principled uncertainty estimates, and can be cheaply updated online, meaning it can request and incorporate new training data when it encounters inputs on which it is uncertain. In experiments, our approach is able to solve learning problems where a single message operator is required for multiple, substantially different data sets (logistic regression for a variety of classification problems), where it is essential to accurately assess uncertainty and to efficiently and robustly update the message operator.