Optimal Online Change Detection via Random Fourier Features

This article studies the problem of online non-parametric change point detection in multivariate data streams. We approach the problem through the lens of kernel-based two-sample testing and introduce a sequential testing procedure based on random Fourier features, running with logarithmic time complexity per observation and with overall logarithmic space complexity. The algorithm has two advantages compared to the state of the art. First, our approach is genuinely online, and no access to training data known to be from the pre-change distribution is necessary. Second, the algorithm does not require the user to specify a window parameter over which local tests are to be calculated. We prove strong theoretical guarantees on the algorithm's performance, including information-theoretic bounds demonstrating that the detection delay is optimal in the minimax sense. Numerical studies on real and synthetic data show that our algorithm is competitive with respect to the state of the art.

Robust Partial-Label Learning by Leveraging Class Activation Values

Real-world training data is often noisy; for example, human annotators assign conflicting class labels to the same instances. Partial-label learning (PLL) is a weakly supervised learning paradigm that allows training classifiers in this context without manual data cleaning. While state-of-the-art methods have good predictive performance, their predictions are sensitive to high noise levels, out-of-distribution data, and adversarial perturbations. We propose a novel PLL method based on subjective logic, which explicitly represents uncertainty by leveraging the magnitudes of the underlying neural network's class activation values. Thereby, we effectively incorporate prior knowledge about the class labels by using a novel label weight re-distribution strategy that we prove to be optimal. We empirically show that our method yields more robust predictions in terms of predictive performance under high PLL noise levels, handling out-of-distribution examples, and handling adversarial perturbations on the test instances.

Partial-Label Learning with Conformal Candidate Cleaning

Real-world data is often ambiguous; for example, human annotation produces instances with multiple conflicting class labels. Partial-label learning (PLL) aims at training a classifier in this challenging setting, where each instance is associated with a set of candidate labels and one correct, but unknown, class label. A multitude of algorithms targeting this setting exists and, to enhance their prediction quality, several extensions that are applicable across a wide range of PLL methods have been introduced. While many of these extensions rely on heuristics, this article proposes a novel enhancing method that incrementally prunes candidate sets using conformal prediction. To work around the missing labeled validation set, which is typically required for conformal prediction, we propose a strategy that alternates between training a PLL classifier to label the validation set, leveraging these predicted class labels for calibration, and pruning candidate labels that are not part of the resulting conformal sets. In this sense, our method alternates between empirical risk minimization and candidate set pruning. We establish that our pruning method preserves the conformal validity with respect to the unknown ground truth. Our extensive experiments on artificial and real-world data show that the proposed approach significantly improves the test set accuracies of several state-of-the-art PLL classifiers.

Nyström Kernel Stein Discrepancy

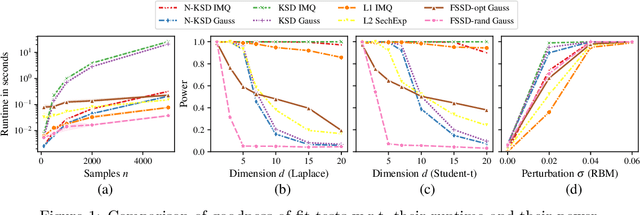
Kernel methods underpin many of the most successful approaches in data science and statistics, and they allow representing probability measures as elements of a reproducing kernel Hilbert space without loss of information. Recently, the kernel Stein discrepancy (KSD), which combines Stein's method with kernel techniques, gained considerable attention. Through the Stein operator, KSD allows the construction of powerful goodness-of-fit tests where it is sufficient to know the target distribution up to a multiplicative constant. However, the typical U- and V-statistic-based KSD estimators suffer from a quadratic runtime complexity, which hinders their application in large-scale settings. In this work, we propose a Nystr\"om-based KSD acceleration -- with runtime $\mathcal O\!\left(mn+m^3\right)$ for $n$ samples and $m\ll n$ Nystr\"om points -- , show its $\sqrt{n}$-consistency under the null with a classical sub-Gaussian assumption, and demonstrate its applicability for goodness-of-fit testing on a suite of benchmarks.

The Minimax Rate of HSIC Estimation for Translation-Invariant Kernels

Kernel techniques are among the most influential approaches in data science and statistics. Under mild conditions, the reproducing kernel Hilbert space associated to a kernel is capable of encoding the independence of $M\ge 2$ random variables. Probably the most widespread independence measure relying on kernels is the so-called Hilbert-Schmidt independence criterion (HSIC; also referred to as distance covariance in the statistics literature). Despite various existing HSIC estimators designed since its introduction close to two decades ago, the fundamental question of the rate at which HSIC can be estimated is still open. In this work, we prove that the minimax optimal rate of HSIC estimation on $\mathbb R^d$ for Borel measures containing the Gaussians with continuous bounded translation-invariant characteristic kernels is $\mathcal O\!\left(n^{-1/2}\right)$. Specifically, our result implies the optimality in the minimax sense of many of the most-frequently used estimators (including the U-statistic, the V-statistic, and the Nystr\"om-based one) on $\mathbb R^d$.

Uncertainty-Aware Partial-Label Learning

In real-world applications, one often encounters ambiguously labeled data, where different annotators assign conflicting class labels. Partial-label learning allows training classifiers in this weakly supervised setting. While state-of-the-art methods already feature good predictive performance, they often suffer from miscalibrated uncertainty estimates. However, having well-calibrated uncertainty estimates is important, especially in safety-critical domains like medicine and autonomous driving. In this article, we propose a novel nearest-neighbor-based partial-label-learning algorithm that leverages Dempster-Shafer theory. Extensive experiments on artificial and real-world datasets show that the proposed method provides a well-calibrated uncertainty estimate and achieves competitive prediction performance. Additionally, we prove that our algorithm is risk-consistent.

Adaptive Bernstein Change Detector for High-Dimensional Data Streams

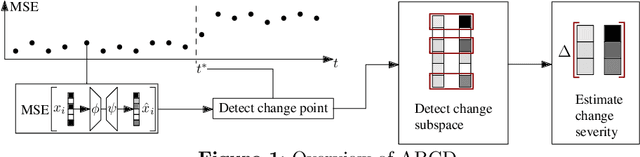
Change detection is of fundamental importance when analyzing data streams. Detecting changes both quickly and accurately enables monitoring and prediction systems to react, e.g., by issuing an alarm or by updating a learning algorithm. However, detecting changes is challenging when observations are high-dimensional. In high-dimensional data, change detectors should not only be able to identify when changes happen, but also in which subspace they occur. Ideally, one should also quantify how severe they are. Our approach, ABCD, has these properties. ABCD learns an encoder-decoder model and monitors its accuracy over a window of adaptive size. ABCD derives a change score based on Bernstein's inequality to detect deviations in terms of accuracy, which indicate changes. Our experiments demonstrate that ABCD outperforms its best competitor by at least 8% and up to 23% in F1-score on average. It can also accurately estimate changes' subspace, together with a severity measure that correlates with the ground truth.

Nyström $M$-Hilbert-Schmidt Independence Criterion

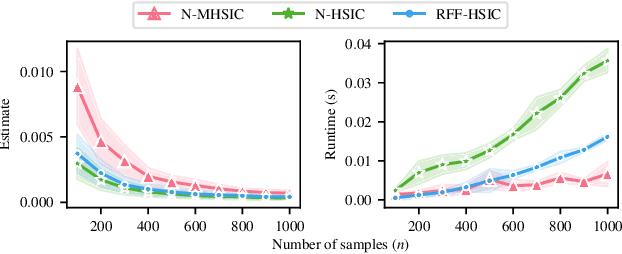
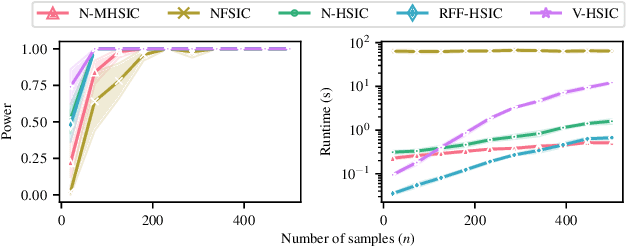
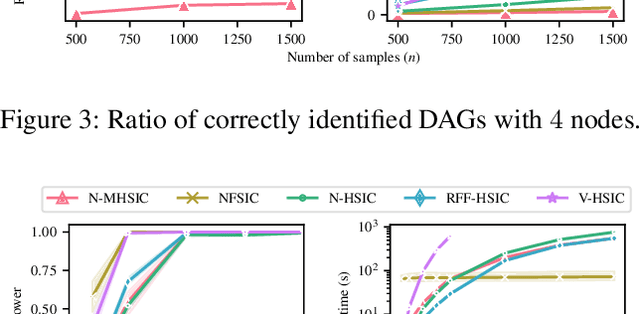
Kernel techniques are among the most popular and powerful approaches of data science. Among the key features that make kernels ubiquitous are (i) the number of domains they have been designed for, (ii) the Hilbert structure of the function class associated to kernels facilitating their statistical analysis, and (iii) their ability to represent probability distributions without loss of information. These properties give rise to the immense success of Hilbert-Schmidt independence criterion (HSIC) which is able to capture joint independence of random variables under mild conditions, and permits closed-form estimators with quadratic computational complexity (w.r.t. the sample size). In order to alleviate the quadratic computational bottleneck in large-scale applications, multiple HSIC approximations have been proposed, however these estimators are restricted to $M=2$ random variables, do not extend naturally to the $M\ge 2$ case, and lack theoretical guarantees. In this work, we propose an alternative Nystr\"om-based HSIC estimator which handles the $M\ge 2$ case, prove its consistency, and demonstrate its applicability in multiple contexts, including synthetic examples, dependency testing of media annotations, and causal discovery.

Scalable Online Change Detection for High-dimensional Data Streams

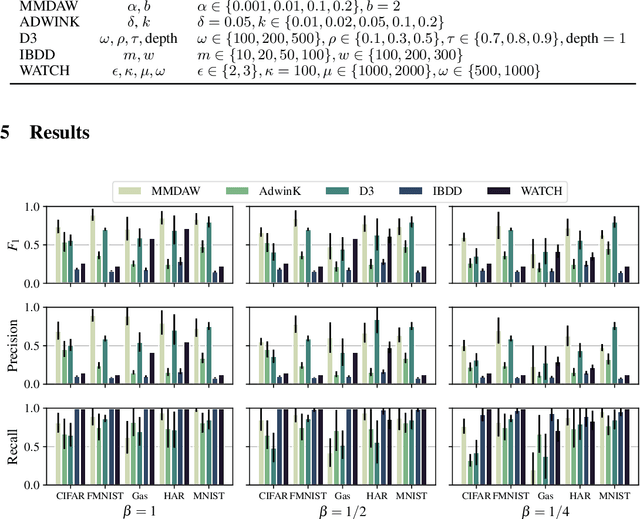
Detecting changes in data streams is a core objective in their analysis and has applications in, say, predictive maintenance, fraud detection, and medicine. A principled approach to detect changes is to compare distributions observed within the stream to each other. However, data streams often are high-dimensional, and changes can be complex, e.g., only manifest themselves in higher moments. The streaming setting also imposes heavy memory and computation restrictions. We propose an algorithm, Maximum Mean Discrepancy Adaptive Windowing (MMDAW), which leverages the well-known Maximum Mean Discrepancy (MMD) two-sample test, and facilitates its efficient online computation on windows whose size it flexibly adapts. As MMD is sensitive to any change in the underlying distribution, our algorithm is a general-purpose non-parametric change detector that fulfills the requirements imposed by the streaming setting. Our experiments show that MMDAW achieves better detection quality than state-of-the-art competitors.

Efficient Subspace Search in Data Streams

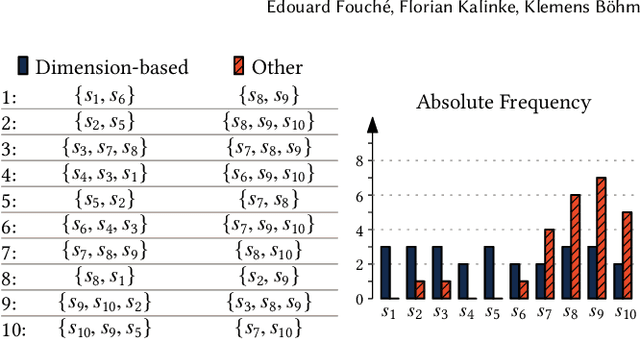
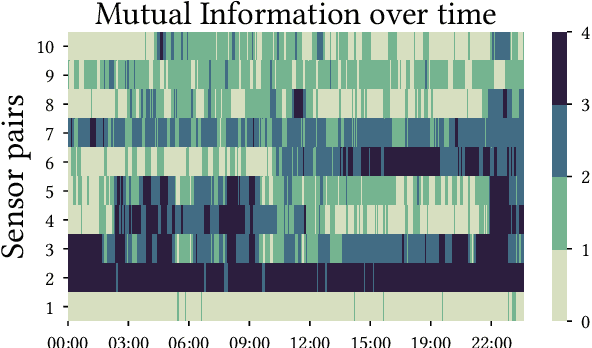
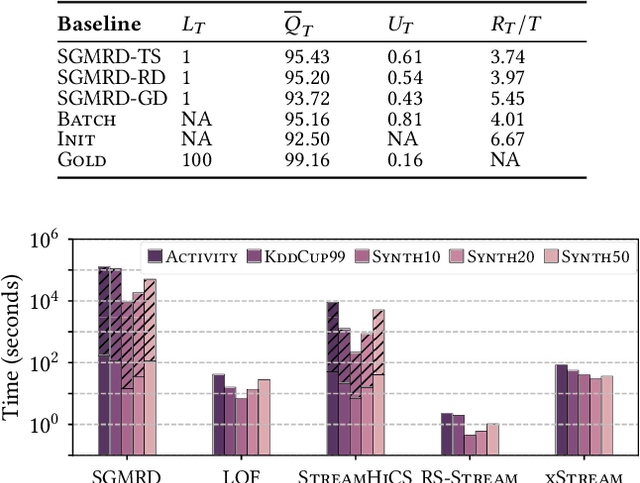
In the real world, data streams are ubiquitous -- think of network traffic or sensor data. Mining patterns, e.g., outliers or clusters, from such data must take place in real time. This is challenging because (1) streams often have high dimensionality, and (2) the data characteristics may change over time. Existing approaches tend to focus on only one aspect, either high dimensionality or the specifics of the streaming setting. For static data, a common approach to deal with high dimensionality -- known as subspace search -- extracts low-dimensional, `interesting' projections (subspaces), in which patterns are easier to find. In this paper, we address both Challenge (1) and (2) by generalising subspace search to data streams. Our approach, Streaming Greedy Maximum Random Deviation (SGMRD), monitors interesting subspaces in high-dimensional data streams. It leverages novel multivariate dependency estimators and monitoring techniques based on bandit theory. We show that the benefits of SGMRD are twofold: (i) It monitors subspaces efficiently, and (ii) this improves the results of downstream data mining tasks, such as outlier detection. Our experiments, performed against synthetic and real-world data, demonstrate that SGMRD outperforms its competitors by a large margin.