Adaptive Bernstein Change Detector for High-Dimensional Data Streams

Change detection is of fundamental importance when analyzing data streams. Detecting changes both quickly and accurately enables monitoring and prediction systems to react, e.g., by issuing an alarm or by updating a learning algorithm. However, detecting changes is challenging when observations are high-dimensional. In high-dimensional data, change detectors should not only be able to identify when changes happen, but also in which subspace they occur. Ideally, one should also quantify how severe they are. Our approach, ABCD, has these properties. ABCD learns an encoder-decoder model and monitors its accuracy over a window of adaptive size. ABCD derives a change score based on Bernstein's inequality to detect deviations in terms of accuracy, which indicate changes. Our experiments demonstrate that ABCD outperforms its best competitor by at least 8% and up to 23% in F1-score on average. It can also accurately estimate changes' subspace, together with a severity measure that correlates with the ground truth.

Budgeted Multi-Armed Bandits with Asymmetric Confidence Intervals

We study the stochastic Budgeted Multi-Armed Bandit (MAB) problem, where a player chooses from $K$ arms with unknown expected rewards and costs. The goal is to maximize the total reward under a budget constraint. A player thus seeks to choose the arm with the highest reward-cost ratio as often as possible. Current state-of-the-art policies for this problem have several issues, which we illustrate. To overcome them, we propose a new upper confidence bound (UCB) sampling policy, $\omega$-UCB, that uses asymmetric confidence intervals. These intervals scale with the distance between the sample mean and the bounds of a random variable, yielding a more accurate and tight estimation of the reward-cost ratio compared to our competitors. We show that our approach has logarithmic regret and consistently outperforms existing policies in synthetic and real settings.

Scalable Online Change Detection for High-dimensional Data Streams

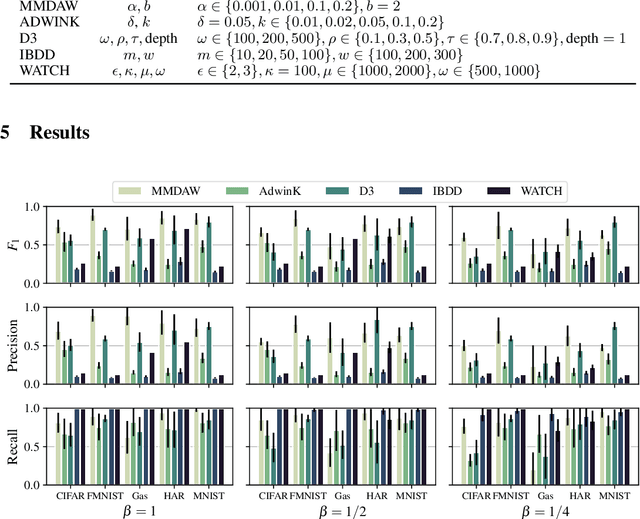
Detecting changes in data streams is a core objective in their analysis and has applications in, say, predictive maintenance, fraud detection, and medicine. A principled approach to detect changes is to compare distributions observed within the stream to each other. However, data streams often are high-dimensional, and changes can be complex, e.g., only manifest themselves in higher moments. The streaming setting also imposes heavy memory and computation restrictions. We propose an algorithm, Maximum Mean Discrepancy Adaptive Windowing (MMDAW), which leverages the well-known Maximum Mean Discrepancy (MMD) two-sample test, and facilitates its efficient online computation on windows whose size it flexibly adapts. As MMD is sensitive to any change in the underlying distribution, our algorithm is a general-purpose non-parametric change detector that fulfills the requirements imposed by the streaming setting. Our experiments show that MMDAW achieves better detection quality than state-of-the-art competitors.

Finite-time Analysis of Globally Nonstationary Multi-Armed Bandits

We consider nonstationary multi-armed bandit problems where the model parameters of the arms change over time. We introduce the adaptive resetting bandit (ADR-bandit), which is a class of bandit algorithms that leverages adaptive windowing techniques from the data stream community. We first provide new guarantees on the quality of estimators resulting from adaptive windowing techniques, which are of independent interest in the data mining community. Furthermore, we conduct a finite-time analysis of ADR-bandit in two typical environments: an abrupt environment where changes occur instantaneously and a gradual environment where changes occur progressively. We demonstrate that ADR-bandit has nearly optimal performance when the abrupt or global changes occur in a coordinated manner that we call global changes. We demonstrate that forced exploration is unnecessary when we restrict the interest to the global changes. Unlike the existing nonstationary bandit algorithms, ADR-bandit has optimal performance in stationary environments as well as nonstationary environments with global changes. Our experiments show that the proposed algorithms outperform the existing approaches in synthetic and real-world environments.

Efficient Subspace Search in Data Streams

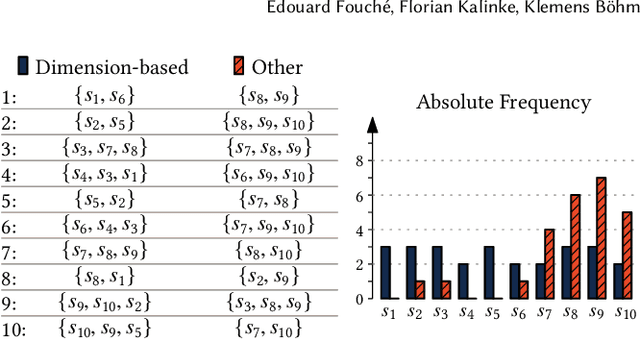
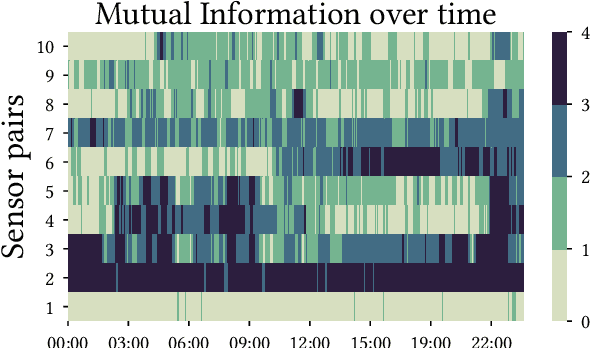
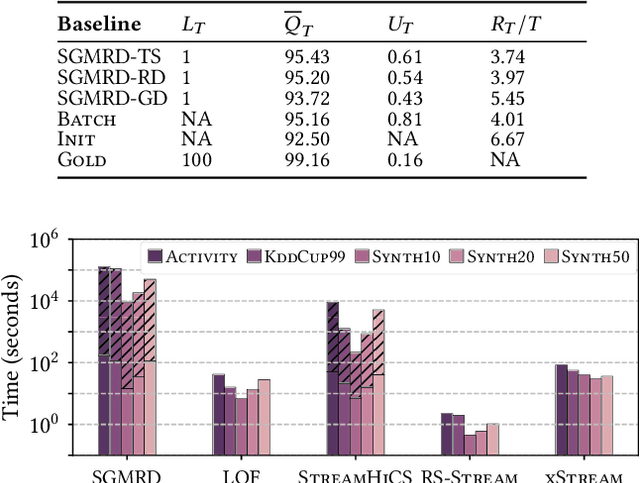
In the real world, data streams are ubiquitous -- think of network traffic or sensor data. Mining patterns, e.g., outliers or clusters, from such data must take place in real time. This is challenging because (1) streams often have high dimensionality, and (2) the data characteristics may change over time. Existing approaches tend to focus on only one aspect, either high dimensionality or the specifics of the streaming setting. For static data, a common approach to deal with high dimensionality -- known as subspace search -- extracts low-dimensional, `interesting' projections (subspaces), in which patterns are easier to find. In this paper, we address both Challenge (1) and (2) by generalising subspace search to data streams. Our approach, Streaming Greedy Maximum Random Deviation (SGMRD), monitors interesting subspaces in high-dimensional data streams. It leverages novel multivariate dependency estimators and monitoring techniques based on bandit theory. We show that the benefits of SGMRD are twofold: (i) It monitors subspaces efficiently, and (ii) this improves the results of downstream data mining tasks, such as outlier detection. Our experiments, performed against synthetic and real-world data, demonstrate that SGMRD outperforms its competitors by a large margin.