CapyMOA: Efficient Machine Learning for Data Streams in Python

CapyMOA is an open-source library designed for efficient machine learning on streaming data. It provides a structured framework for real-time learning and evaluation, featuring a flexible data representation. CapyMOA includes an extensible architecture that allows integration with external frameworks such as MOA and PyTorch, facilitating hybrid learning approaches that combine traditional online algorithms with deep learning techniques. By emphasizing adaptability, scalability, and usability, CapyMOA allows researchers and practitioners to tackle dynamic learning challenges across various domains.

Generalizability of experimental studies

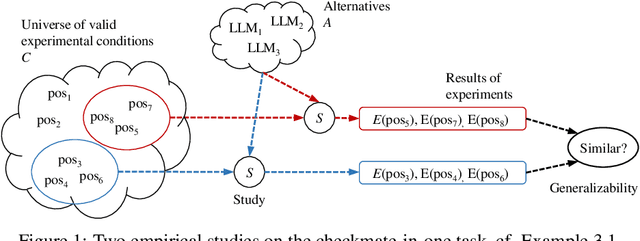
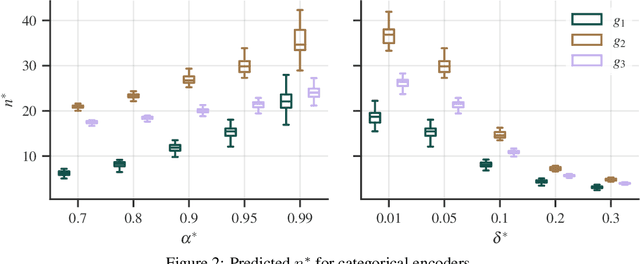
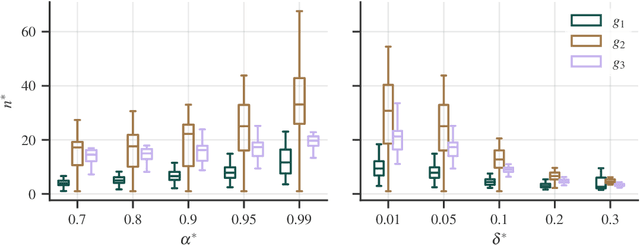
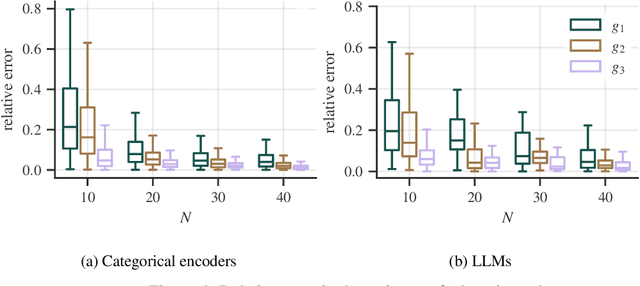
Experimental studies are a cornerstone of machine learning (ML) research. A common, but often implicit, assumption is that the results of a study will generalize beyond the study itself, e.g. to new data. That is, there is a high probability that repeating the study under different conditions will yield similar results. Despite the importance of the concept, the problem of measuring generalizability remains open. This is probably due to the lack of a mathematical formalization of experimental studies. In this paper, we propose such a formalization and develop a quantifiable notion of generalizability. This notion allows to explore the generalizability of existing studies and to estimate the number of experiments needed to achieve the generalizability of new studies. To demonstrate its usefulness, we apply it to two recently published benchmarks to discern generalizable and non-generalizable results. We also publish a Python module that allows our analysis to be repeated for other experimental studies.

Adaptive Bernstein Change Detector for High-Dimensional Data Streams

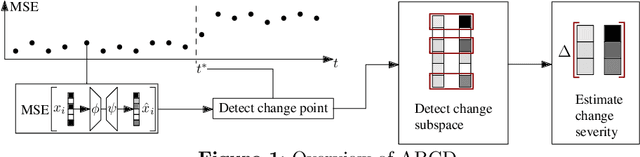
Change detection is of fundamental importance when analyzing data streams. Detecting changes both quickly and accurately enables monitoring and prediction systems to react, e.g., by issuing an alarm or by updating a learning algorithm. However, detecting changes is challenging when observations are high-dimensional. In high-dimensional data, change detectors should not only be able to identify when changes happen, but also in which subspace they occur. Ideally, one should also quantify how severe they are. Our approach, ABCD, has these properties. ABCD learns an encoder-decoder model and monitors its accuracy over a window of adaptive size. ABCD derives a change score based on Bernstein's inequality to detect deviations in terms of accuracy, which indicate changes. Our experiments demonstrate that ABCD outperforms its best competitor by at least 8% and up to 23% in F1-score on average. It can also accurately estimate changes' subspace, together with a severity measure that correlates with the ground truth.

Budgeted Multi-Armed Bandits with Asymmetric Confidence Intervals

We study the stochastic Budgeted Multi-Armed Bandit (MAB) problem, where a player chooses from $K$ arms with unknown expected rewards and costs. The goal is to maximize the total reward under a budget constraint. A player thus seeks to choose the arm with the highest reward-cost ratio as often as possible. Current state-of-the-art policies for this problem have several issues, which we illustrate. To overcome them, we propose a new upper confidence bound (UCB) sampling policy, $\omega$-UCB, that uses asymmetric confidence intervals. These intervals scale with the distance between the sample mean and the bounds of a random variable, yielding a more accurate and tight estimation of the reward-cost ratio compared to our competitors. We show that our approach has logarithmic regret and consistently outperforms existing policies in synthetic and real settings.

Scalable Online Change Detection for High-dimensional Data Streams

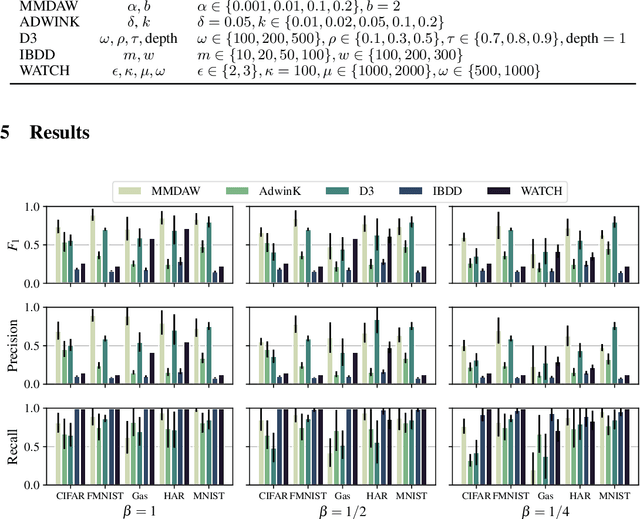
Detecting changes in data streams is a core objective in their analysis and has applications in, say, predictive maintenance, fraud detection, and medicine. A principled approach to detect changes is to compare distributions observed within the stream to each other. However, data streams often are high-dimensional, and changes can be complex, e.g., only manifest themselves in higher moments. The streaming setting also imposes heavy memory and computation restrictions. We propose an algorithm, Maximum Mean Discrepancy Adaptive Windowing (MMDAW), which leverages the well-known Maximum Mean Discrepancy (MMD) two-sample test, and facilitates its efficient online computation on windows whose size it flexibly adapts. As MMD is sensitive to any change in the underlying distribution, our algorithm is a general-purpose non-parametric change detector that fulfills the requirements imposed by the streaming setting. Our experiments show that MMDAW achieves better detection quality than state-of-the-art competitors.