Kernelized Cumulants: Beyond Kernel Mean Embeddings

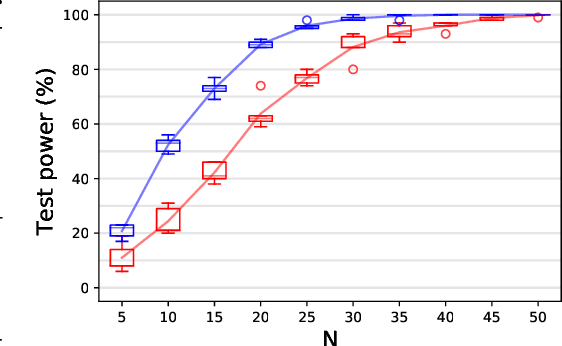
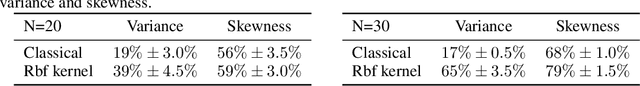
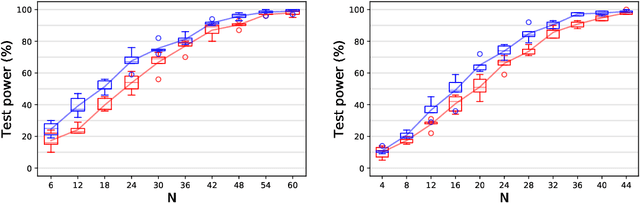
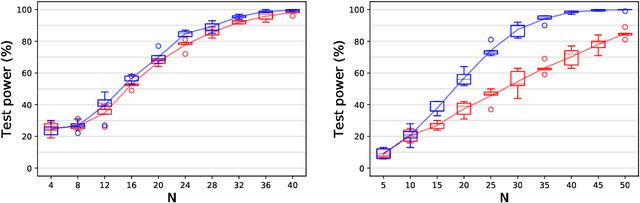
In $\mathbb R^d$, it is well-known that cumulants provide an alternative to moments that can achieve the same goals with numerous benefits such as lower variance estimators. In this paper we extend cumulants to reproducing kernel Hilbert spaces (RKHS) using tools from tensor algebras and show that they are computationally tractable by a kernel trick. These kernelized cumulants provide a new set of all-purpose statistics; the classical maximum mean discrepancy and Hilbert-Schmidt independence criterion arise as the degree one objects in our general construction. We argue both theoretically and empirically (on synthetic, environmental, and traffic data analysis) that going beyond degree one has several advantages and can be achieved with the same computational complexity and minimal overhead in our experiments.

Seq2Tens: An Efficient Representation of Sequences by Low-Rank Tensor Projections

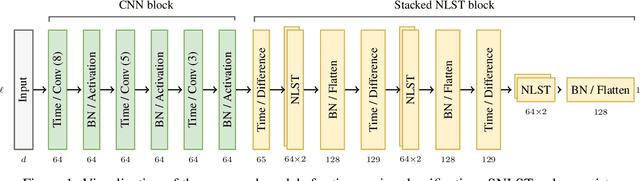
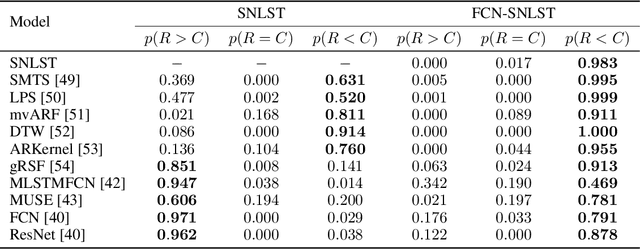
Sequential data such as time series, video, or text can be challenging to analyse as the ordered structure gives rise to complex dependencies. At the heart of this is non-commutativity, in the sense that reordering the elements of a sequence can completely change its meaning. We use a classical mathematical object -- the tensor algebra -- to capture such dependencies. To address the innate computational complexity of high degree tensors, we use compositions of low-rank tensor projections. This yields modular and scalable building blocks for neural networks that give state-of-the-art performance on standard benchmarks such as multivariate time series classification and generative models for video.

Deep Signatures

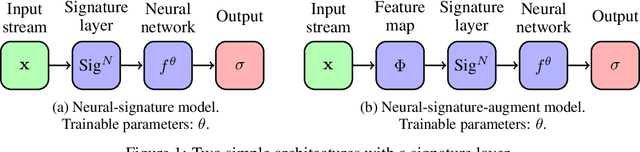
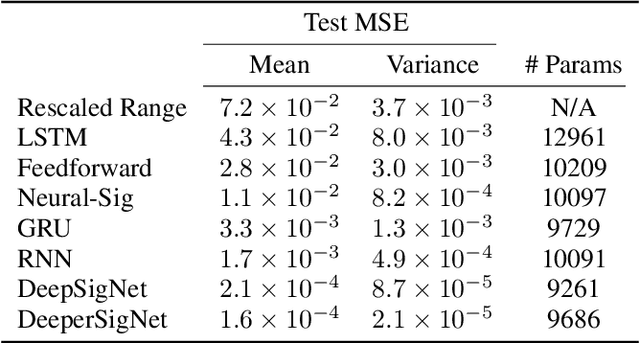
The signature is an infinite graded sequence of statistics known to characterise a stream of data up to a negligible equivalence class. It is a transform which has previously been treated as a fixed feature transformation, on top of which a model may be built. We propose a novel approach which combines the advantages of the signature transform with modern deep learning frameworks. By learning an augmentation of the stream prior to the signature transform, the terms of the signature may be selected in a data-dependent way. More generally, we describe how the signature transform may be used as a layer anywhere within a neural network. In this context it may be interpreted as an activation function not operating element-wise. We present the results of empirical experiments to back up the theoretical justification. Code available at github.com/patrick-kidger/Deep-Signatures.