Single-seed generation of Brownian paths and integrals for adaptive and high order SDE solvers

Despite the success of adaptive time-stepping in ODE simulation, it has so far seen few applications for Stochastic Differential Equations (SDEs). To simulate SDEs adaptively, methods such as the Virtual Brownian Tree (VBT) have been developed, which can generate Brownian motion (BM) non-chronologically. However, in most applications, knowing only the values of Brownian motion is not enough to achieve a high order of convergence; for that, we must compute time-integrals of BM such as $\int_s^t W_r \, dr$. With the aim of using high order SDE solvers adaptively, we extend the VBT to generate these integrals of BM in addition to the Brownian increments. A JAX-based implementation of our construction is included in the popular Diffrax library (https://github.com/patrick-kidger/diffrax). Since the entire Brownian path produced by VBT is uniquely determined by a single PRNG seed, previously generated samples need not be stored, which results in a constant memory footprint and enables experiment repeatability and strong error estimation. Based on binary search, the VBT's time complexity is logarithmic in the tolerance parameter $\varepsilon$. Unlike the original VBT algorithm, which was only precise at some dyadic times, we prove that our construction exactly matches the joint distribution of the Brownian motion and its time integrals at any query times, provided they are at least $\varepsilon$ apart. We present two applications of adaptive high order solvers enabled by our new VBT. Using adaptive solvers to simulate a high-volatility CIR model, we achieve more than twice the convergence order of constant stepping. We apply an adaptive third order underdamped or kinetic Langevin solver to an MCMC problem, where our approach outperforms the No U-Turn Sampler, while using only a tenth of its function evaluations.

On Neural Differential Equations

The conjoining of dynamical systems and deep learning has become a topic of great interest. In particular, neural differential equations (NDEs) demonstrate that neural networks and differential equation are two sides of the same coin. Traditional parameterised differential equations are a special case. Many popular neural network architectures, such as residual networks and recurrent networks, are discretisations. NDEs are suitable for tackling generative problems, dynamical systems, and time series (particularly in physics, finance, ...) and are thus of interest to both modern machine learning and traditional mathematical modelling. NDEs offer high-capacity function approximation, strong priors on model space, the ability to handle irregular data, memory efficiency, and a wealth of available theory on both sides. This doctoral thesis provides an in-depth survey of the field. Topics include: neural ordinary differential equations (e.g. for hybrid neural/mechanistic modelling of physical systems); neural controlled differential equations (e.g. for learning functions of irregular time series); and neural stochastic differential equations (e.g. to produce generative models capable of representing complex stochastic dynamics, or sampling from complex high-dimensional distributions). Further topics include: numerical methods for NDEs (e.g. reversible differential equations solvers, backpropagation through differential equations, Brownian reconstruction); symbolic regression for dynamical systems (e.g. via regularised evolution); and deep implicit models (e.g. deep equilibrium models, differentiable optimisation). We anticipate this thesis will be of interest to anyone interested in the marriage of deep learning with dynamical systems, and hope it will provide a useful reference for the current state of the art.

Equinox: neural networks in JAX via callable PyTrees and filtered transformations

JAX and PyTorch are two popular Python autodifferentiation frameworks. JAX is based around pure functions and functional programming. PyTorch has popularised the use of an object-oriented (OO) class-based syntax for defining parameterised functions, such as neural networks. That this seems like a fundamental difference means current libraries for building parameterised functions in JAX have either rejected the OO approach entirely (Stax) or have introduced OO-to-functional transformations, multiple new abstractions, and been limited in the extent to which they integrate with JAX (Flax, Haiku, Objax). Either way this OO/functional difference has been a source of tension. Here, we introduce `Equinox', a small neural network library showing how a PyTorch-like class-based approach may be admitted without sacrificing JAX-like functional programming. We provide two main ideas. One: parameterised functions are themselves represented as `PyTrees', which means that the parameterisation of a function is transparent to the JAX framework. Two: we filter a PyTree to isolate just those components that should be treated when transforming (`jit', `grad' or `vmap'-ing) a higher-order function of a parameterised function -- such as a loss function applied to a model. Overall Equinox resolves the above tension without introducing any new programmatic abstractions: only PyTrees and transformations, just as with regular JAX. Equinox is available at \url{https://github.com/patrick-kidger/equinox}.

Neural Controlled Differential Equations for Online Prediction Tasks

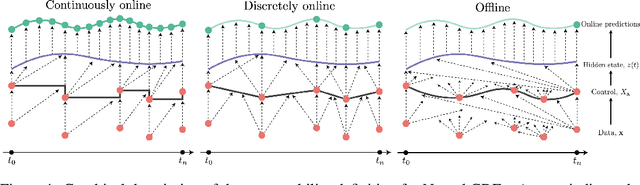
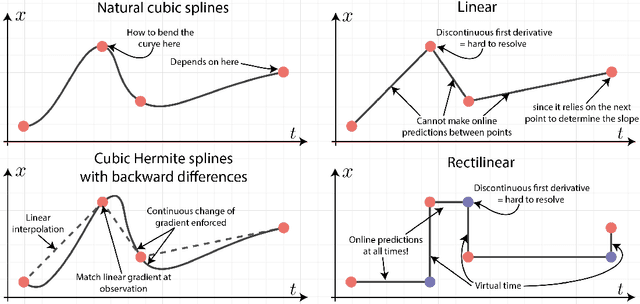
Neural controlled differential equations (Neural CDEs) are a continuous-time extension of recurrent neural networks (RNNs), achieving state-of-the-art (SOTA) performance at modelling functions of irregular time series. In order to interpret discrete data in continuous time, current implementations rely on non-causal interpolations of the data. This is fine when the whole time series is observed in advance, but means that Neural CDEs are not suitable for use in \textit{online prediction tasks}, where predictions need to be made in real-time: a major use case for recurrent networks. Here, we show how this limitation may be rectified. First, we identify several theoretical conditions that interpolation schemes for Neural CDEs should satisfy, such as boundedness and uniqueness. Second, we use these to motivate the introduction of new schemes that address these conditions, offering in particular measurability (for online prediction), and smoothness (for speed). Third, we empirically benchmark our online Neural CDE model on three continuous monitoring tasks from the MIMIC-IV medical database: we demonstrate improved performance on all tasks against ODE benchmarks, and on two of the three tasks against SOTA non-ODE benchmarks.

Efficient and Accurate Gradients for Neural SDEs

Neural SDEs combine many of the best qualities of both RNNs and SDEs: memory efficient training, high-capacity function approximation, and strong priors on model space. This makes them a natural choice for modelling many types of temporal dynamics. Training a Neural SDE (either as a VAE or as a GAN) requires backpropagating through an SDE solve. This may be done by solving a backwards-in-time SDE whose solution is the desired parameter gradients. However, this has previously suffered from severe speed and accuracy issues, due to high computational cost and numerical truncation errors. Here, we overcome these issues through several technical innovations. First, we introduce the \textit{reversible Heun method}. This is a new SDE solver that is \textit{algebraically reversible}: eliminating numerical gradient errors, and the first such solver of which we are aware. Moreover it requires half as many function evaluations as comparable solvers, giving up to a $1.98\times$ speedup. Second, we introduce the \textit{Brownian Interval}: a new, fast, memory efficient, and exact way of sampling \textit{and reconstructing} Brownian motion. With this we obtain up to a $10.6\times$ speed improvement over previous techniques, which in contrast are both approximate and relatively slow. Third, when specifically training Neural SDEs as GANs (Kidger et al. 2021), we demonstrate how SDE-GANs may be trained through careful weight clipping and choice of activation function. This reduces computational cost (giving up to a $1.87\times$ speedup) and removes the numerical truncation errors associated with gradient penalty. Altogether, we outperform the state-of-the-art by substantial margins, with respect to training speed, and with respect to classification, prediction, and MMD test metrics. We have contributed implementations of all of our techniques to the torchsde library to help facilitate their adoption.

Neural SDEs as Infinite-Dimensional GANs

Stochastic differential equations (SDEs) are a staple of mathematical modelling of temporal dynamics. However, a fundamental limitation has been that such models have typically been relatively inflexible, which recent work introducing Neural SDEs has sought to solve. Here, we show that the current classical approach to fitting SDEs may be approached as a special case of (Wasserstein) GANs, and in doing so the neural and classical regimes may be brought together. The input noise is Brownian motion, the output samples are time-evolving paths produced by a numerical solver, and by parameterising a discriminator as a Neural Controlled Differential Equation (CDE), we obtain Neural SDEs as (in modern machine learning parlance) continuous-time generative time series models. Unlike previous work on this problem, this is a direct extension of the classical approach without reference to either prespecified statistics or density functions. Arbitrary drift and diffusions are admissible, so as the Wasserstein loss has a unique global minima, in the infinite data limit \textit{any} SDE may be learnt.

"Hey, that's not an ODE": Faster ODE Adjoints with 12 Lines of Code

Neural differential equations may be trained by backpropagating gradients via the adjoint method, which is another differential equation typically solved using an adaptive-step-size numerical differential equation solver. A proposed step is accepted if its error, \emph{relative to some norm}, is sufficiently small; else it is rejected, the step is shrunk, and the process is repeated. Here, we demonstrate that the particular structure of the adjoint equations makes the usual choices of norm (such as $L^2$) unnecessarily stringent. By replacing it with a more appropriate (semi)norm, fewer steps are unnecessarily rejected and the backpropagation is made faster. This requires only minor code modifications. Experiments on a wide range of tasks---including time series, generative modeling, and physical control---demonstrate a median improvement of 40% fewer function evaluations. On some problems we see as much as 62% fewer function evaluations, so that the overall training time is roughly halved.

Neural CDEs for Long Time Series via the Log-ODE Method

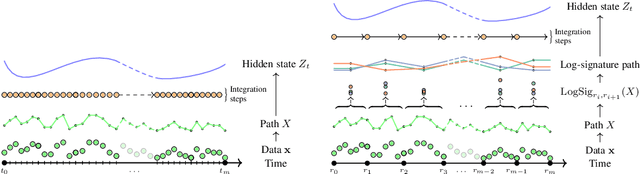
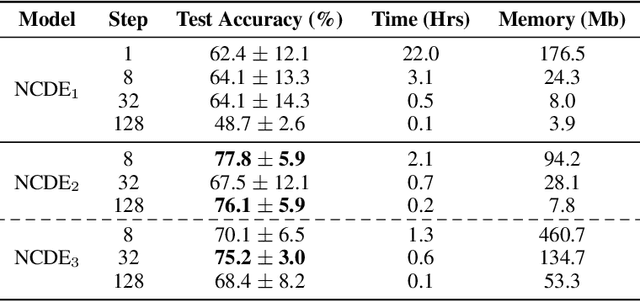
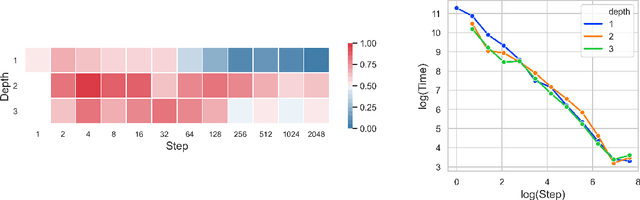
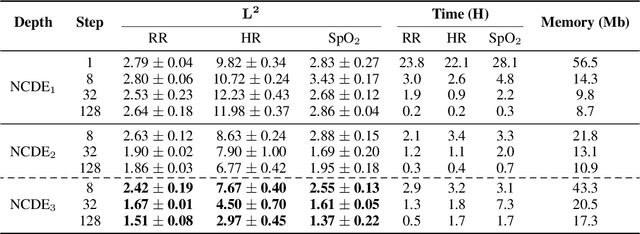
Neural Controlled Differential Equations (Neural CDEs) are the continuous-time analogue of an RNN, just as Neural ODEs are analogous to ResNets. However just like RNNs, training Neural CDEs can be difficult for long time series. Here, we propose to apply a technique drawn from stochastic analysis, namely the log-ODE method. Instead of using the original input sequence, our procedure summarises the information over local time intervals via the log-signature map, and uses the resulting shorter stream of log-signatures as the new input. This represents a length/channel trade-off. In doing so we demonstrate efficacy on problems of length up to 17k observations and observe significant training speed-ups, improvements in model performance, and reduced memory requirements compared to the existing algorithm.

A Generalised Signature Method for Time Series

The `signature method' refers to a collection of feature extraction techniques for multimodal sequential data, derived from the theory of controlled differential equations. Variations exist as many authors have proposed modifications to the method, so as to improve some aspect of it. Here, we introduce a \emph{generalised signature method} that contains these variations as special cases, and groups them conceptually into \emph{augmentations}, \emph{windows}, \emph{transforms}, and \emph{rescalings}. Within this framework we are then able to propose novel variations, and demonstrate how previously distinct options may be combined. We go on to perform an extensive empirical study on 26 datasets as to which aspects of this framework typically produce the best results. Combining the top choices produces a canonical pipeline for the generalised signature method, which demonstrates state-of-the-art accuracy on benchmark problems in multivariate time series classification.

Generalised Interpretable Shapelets for Irregular Time Series

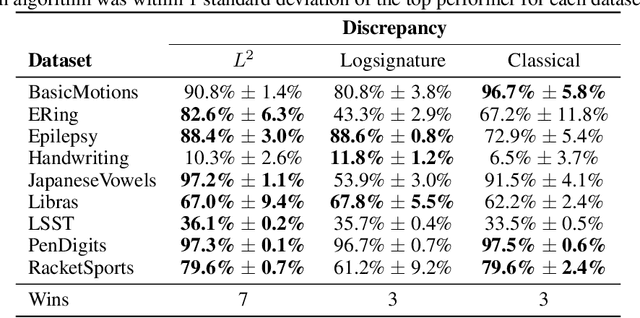
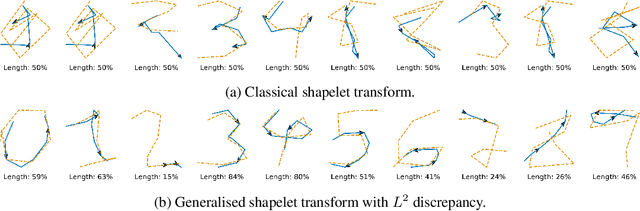
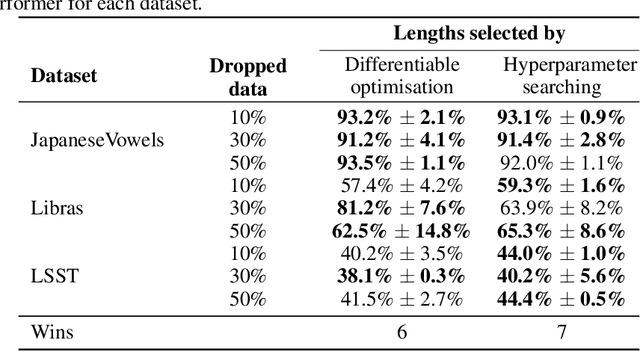
The shapelet transform is a form of feature extraction for time series, in which a time series is described by its similarity to each of a collection of `shapelets'. However it has previously suffered from a number of limitations, such as being limited to regularly-spaced fully-observed time series, and having to choose between efficient training and interpretability. Here, we extend the method to continuous time, and in doing so handle the general case of irregularly-sampled partially-observed multivariate time series. Furthermore, we show that a simple regularisation penalty may be used to train efficiently without sacrificing interpretability. The continuous-time formulation additionally allows for learning the length of each shapelet (previously a discrete object) in a differentiable manner. Finally, we demonstrate that the measure of similarity between time series may be generalised to a learnt pseudometric. We validate our method by demonstrating its performance and interpretability on several datasets; for example we discover (purely from data) that the digits 5 and 6 may be distinguished by the chirality of their bottom loop, and that a kind of spectral gap exists in spoken audio classification.