Generalised Interpretable Shapelets for Irregular Time Series
Paper and Code
May 29, 2020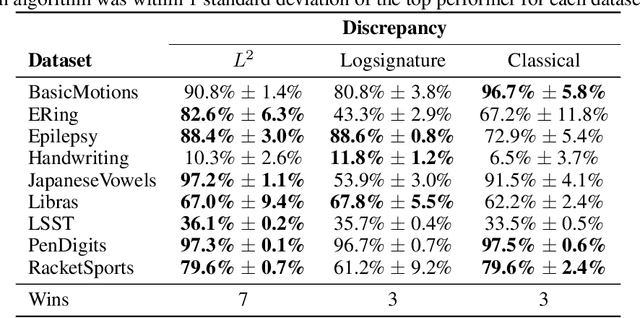
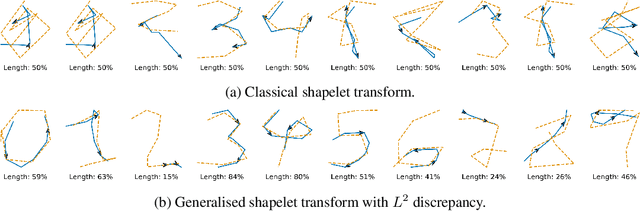
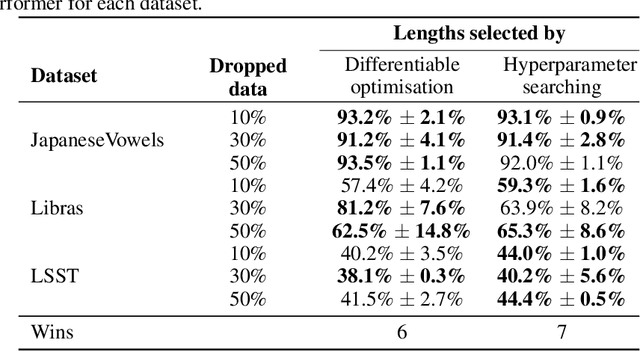

The shapelet transform is a form of feature extraction for time series, in which a time series is described by its similarity to each of a collection of `shapelets'. However it has previously suffered from a number of limitations, such as being limited to regularly-spaced fully-observed time series, and having to choose between efficient training and interpretability. Here, we extend the method to continuous time, and in doing so handle the general case of irregularly-sampled partially-observed multivariate time series. Furthermore, we show that a simple regularisation penalty may be used to train efficiently without sacrificing interpretability. The continuous-time formulation additionally allows for learning the length of each shapelet (previously a discrete object) in a differentiable manner. Finally, we demonstrate that the measure of similarity between time series may be generalised to a learnt pseudometric. We validate our method by demonstrating its performance and interpretability on several datasets; for example we discover (purely from data) that the digits 5 and 6 may be distinguished by the chirality of their bottom loop, and that a kind of spectral gap exists in spoken audio classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge