New directions in the applications of rough path theory

This article provides a concise overview of some of the recent advances in the application of rough path theory to machine learning. Controlled differential equations (CDEs) are discussed as the key mathematical model to describe the interaction of a stream with a physical control system. A collection of iterated integrals known as the signature naturally arises in the description of the response produced by such interactions. The signature comes equipped with a variety of powerful properties rendering it an ideal feature map for streamed data. We summarise recent advances in the symbiosis between deep learning and CDEs, studying the link with RNNs and culminating with the Neural CDE model. We concluded with a discussion on signature kernel methods.

Neural Controlled Differential Equations for Online Prediction Tasks

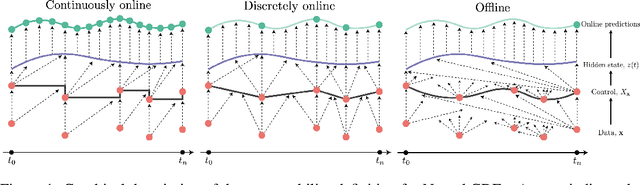
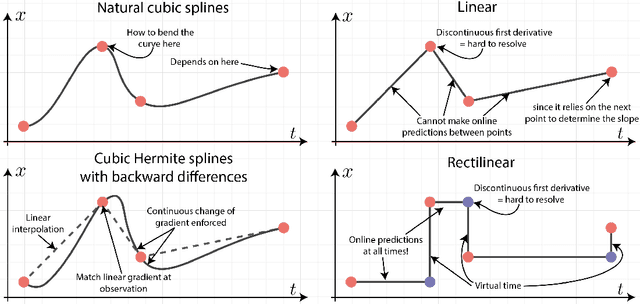
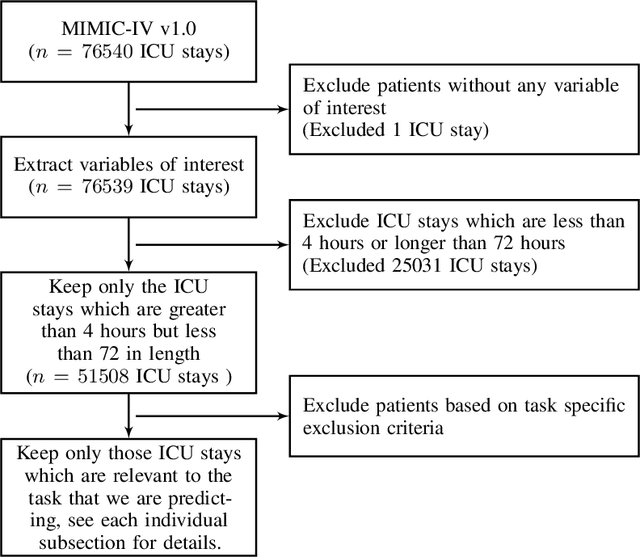
Neural controlled differential equations (Neural CDEs) are a continuous-time extension of recurrent neural networks (RNNs), achieving state-of-the-art (SOTA) performance at modelling functions of irregular time series. In order to interpret discrete data in continuous time, current implementations rely on non-causal interpolations of the data. This is fine when the whole time series is observed in advance, but means that Neural CDEs are not suitable for use in \textit{online prediction tasks}, where predictions need to be made in real-time: a major use case for recurrent networks. Here, we show how this limitation may be rectified. First, we identify several theoretical conditions that interpolation schemes for Neural CDEs should satisfy, such as boundedness and uniqueness. Second, we use these to motivate the introduction of new schemes that address these conditions, offering in particular measurability (for online prediction), and smoothness (for speed). Third, we empirically benchmark our online Neural CDE model on three continuous monitoring tasks from the MIMIC-IV medical database: we demonstrate improved performance on all tasks against ODE benchmarks, and on two of the three tasks against SOTA non-ODE benchmarks.

Neural CDEs for Long Time Series via the Log-ODE Method

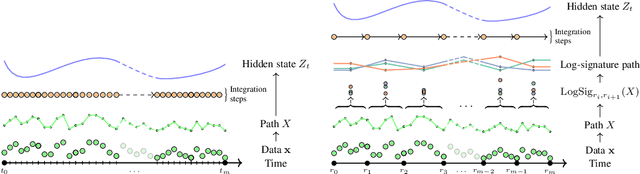
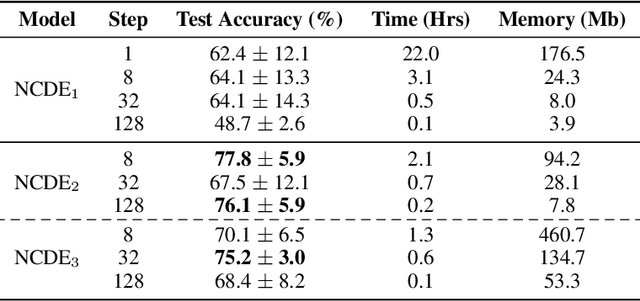
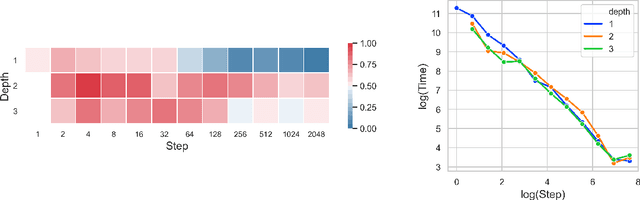
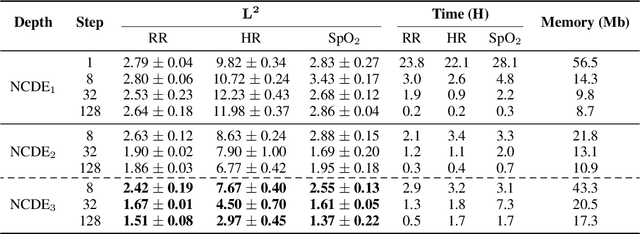
Neural Controlled Differential Equations (Neural CDEs) are the continuous-time analogue of an RNN, just as Neural ODEs are analogous to ResNets. However just like RNNs, training Neural CDEs can be difficult for long time series. Here, we propose to apply a technique drawn from stochastic analysis, namely the log-ODE method. Instead of using the original input sequence, our procedure summarises the information over local time intervals via the log-signature map, and uses the resulting shorter stream of log-signatures as the new input. This represents a length/channel trade-off. In doing so we demonstrate efficacy on problems of length up to 17k observations and observe significant training speed-ups, improvements in model performance, and reduced memory requirements compared to the existing algorithm.

A Generalised Signature Method for Time Series

The `signature method' refers to a collection of feature extraction techniques for multimodal sequential data, derived from the theory of controlled differential equations. Variations exist as many authors have proposed modifications to the method, so as to improve some aspect of it. Here, we introduce a \emph{generalised signature method} that contains these variations as special cases, and groups them conceptually into \emph{augmentations}, \emph{windows}, \emph{transforms}, and \emph{rescalings}. Within this framework we are then able to propose novel variations, and demonstrate how previously distinct options may be combined. We go on to perform an extensive empirical study on 26 datasets as to which aspects of this framework typically produce the best results. Combining the top choices produces a canonical pipeline for the generalised signature method, which demonstrates state-of-the-art accuracy on benchmark problems in multivariate time series classification.

Generalised Interpretable Shapelets for Irregular Time Series

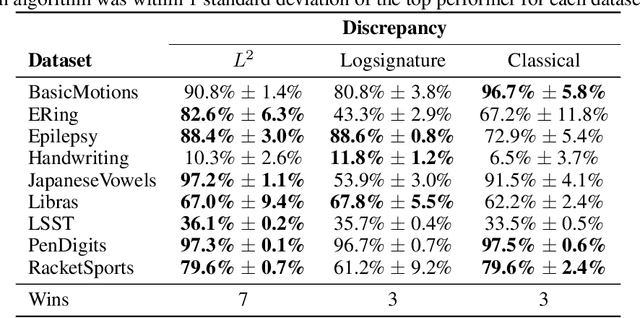
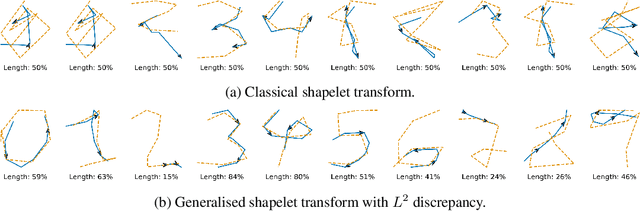
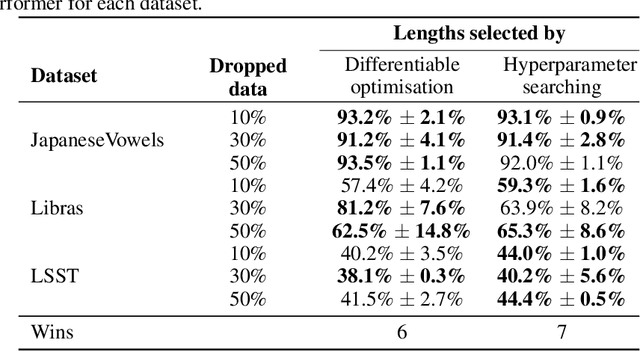
The shapelet transform is a form of feature extraction for time series, in which a time series is described by its similarity to each of a collection of `shapelets'. However it has previously suffered from a number of limitations, such as being limited to regularly-spaced fully-observed time series, and having to choose between efficient training and interpretability. Here, we extend the method to continuous time, and in doing so handle the general case of irregularly-sampled partially-observed multivariate time series. Furthermore, we show that a simple regularisation penalty may be used to train efficiently without sacrificing interpretability. The continuous-time formulation additionally allows for learning the length of each shapelet (previously a discrete object) in a differentiable manner. Finally, we demonstrate that the measure of similarity between time series may be generalised to a learnt pseudometric. We validate our method by demonstrating its performance and interpretability on several datasets; for example we discover (purely from data) that the digits 5 and 6 may be distinguished by the chirality of their bottom loop, and that a kind of spectral gap exists in spoken audio classification.

Neural Controlled Differential Equations for Irregular Time Series

Neural ordinary differential equations are an attractive option for modelling temporal dynamics. However, a fundamental issue is that the solution to an ordinary differential equation is determined by its initial condition, and there is no mechanism for adjusting the trajectory based on subsequent observations. Here, we demonstrate how this may be resolved through the well-understood mathematics of \emph{controlled differential equations}. The resulting \emph{neural controlled differential equation} model is directly applicable to the general setting of partially-observed irregularly-sampled multivariate time series, and (unlike previous work on this problem) it may utilise memory-efficient adjoint-based backpropagation even across observations. We demonstrate that our model achieves state-of-the-art performance against similar (ODE or RNN based) models in empirical studies on a range of datasets. Finally we provide theoretical results demonstrating universal approximation, and that our model subsumes alternative ODE models.