Multivariate Online Linear Regression for Hierarchical Forecasting

In this paper, we consider a deterministic online linear regression model where we allow the responses to be multivariate. To address this problem, we introduce MultiVAW, a method that extends the well-known Vovk-Azoury-Warmuth algorithm to the multivariate setting, and show that it also enjoys logarithmic regret in time. We apply our results to the online hierarchical forecasting problem and recover an algorithm from this literature as a special case, allowing us to relax the hypotheses usually made for its analysis.

Non-asymptotic Analysis of Biased Adaptive Stochastic Approximation

Stochastic Gradient Descent (SGD) with adaptive steps is now widely used for training deep neural networks. Most theoretical results assume access to unbiased gradient estimators, which is not the case in several recent deep learning and reinforcement learning applications that use Monte Carlo methods. This paper provides a comprehensive non-asymptotic analysis of SGD with biased gradients and adaptive steps for convex and non-convex smooth functions. Our study incorporates time-dependent bias and emphasizes the importance of controlling the bias and Mean Squared Error (MSE) of the gradient estimator. In particular, we establish that Adagrad and RMSProp with biased gradients converge to critical points for smooth non-convex functions at a rate similar to existing results in the literature for the unbiased case. Finally, we provide experimental results using Variational Autoenconders (VAE) that illustrate our convergence results and show how the effect of bias can be reduced by appropriate hyperparameter tuning.

Dynamical Survival Analysis with Controlled Latent States

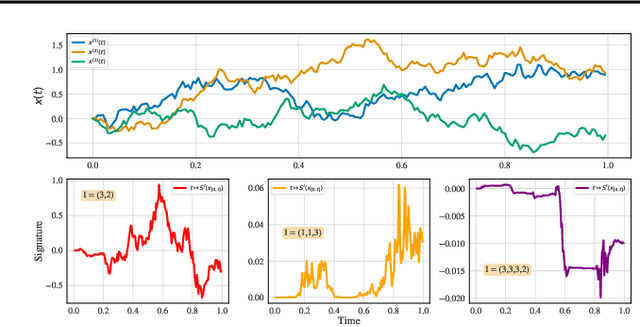
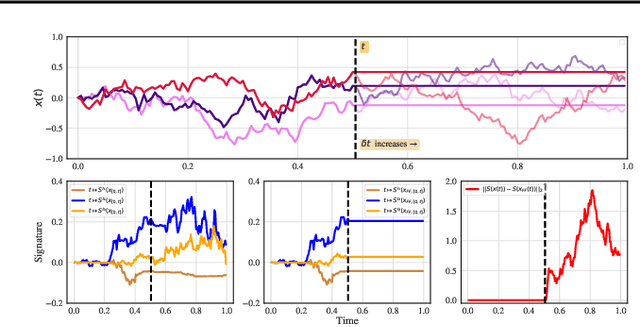
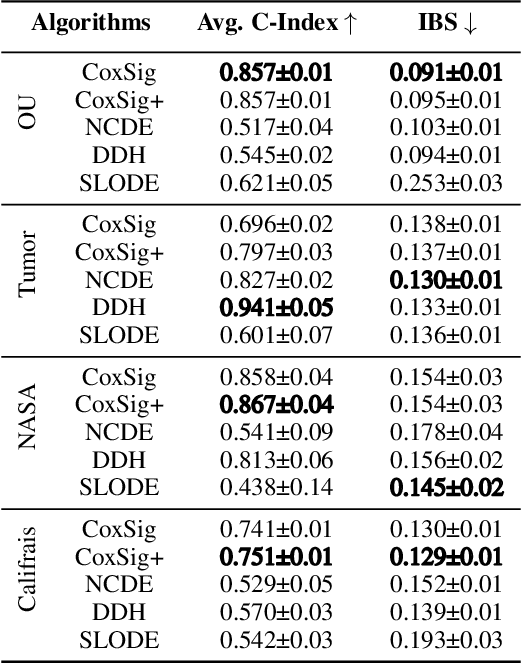
We consider the task of learning individual-specific intensities of counting processes from a set of static variables and irregularly sampled time series. We introduce a novel modelization approach in which the intensity is the solution to a controlled differential equation. We first design a neural estimator by building on neural controlled differential equations. In a second time, we show that our model can be linearized in the signature space under sufficient regularity conditions, yielding a signature-based estimator which we call CoxSig. We provide theoretical learning guarantees for both estimators, before showcasing the performance of our models on a vast array of simulated and real-world datasets from finance, predictive maintenance and food supply chain management.

New directions in the applications of rough path theory

This article provides a concise overview of some of the recent advances in the application of rough path theory to machine learning. Controlled differential equations (CDEs) are discussed as the key mathematical model to describe the interaction of a stream with a physical control system. A collection of iterated integrals known as the signature naturally arises in the description of the response produced by such interactions. The signature comes equipped with a variety of powerful properties rendering it an ideal feature map for streamed data. We summarise recent advances in the symbiosis between deep learning and CDEs, studying the link with RNNs and culminating with the Neural CDE model. We concluded with a discussion on signature kernel methods.

Learning the Dynamics of Sparsely Observed Interacting Systems

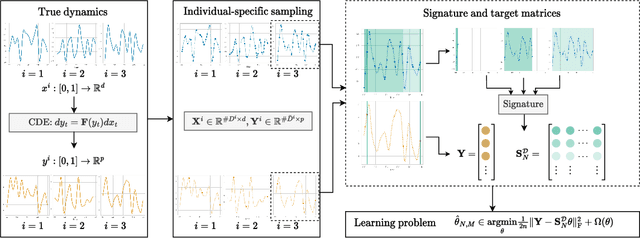
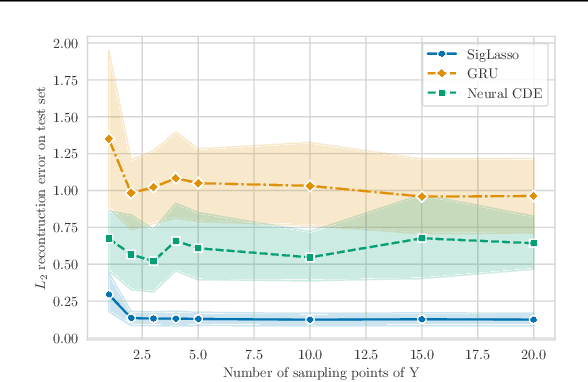
We address the problem of learning the dynamics of an unknown non-parametric system linking a target and a feature time series. The feature time series is measured on a sparse and irregular grid, while we have access to only a few points of the target time series. Once learned, we can use these dynamics to predict values of the target from the previous values of the feature time series. We frame this task as learning the solution map of a controlled differential equation (CDE). By leveraging the rich theory of signatures, we are able to cast this non-linear problem as a high-dimensional linear regression. We provide an oracle bound on the prediction error which exhibits explicit dependencies on the individual-specific sampling schemes. Our theoretical results are illustrated by simulations which show that our method outperforms existing algorithms for recovering the full time series while being computationally cheap. We conclude by demonstrating its potential on real-world epidemiological data.

Scaling ResNets in the Large-depth Regime

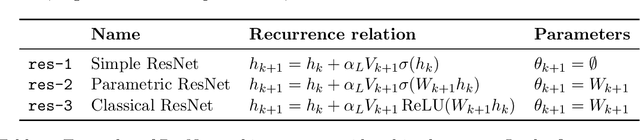
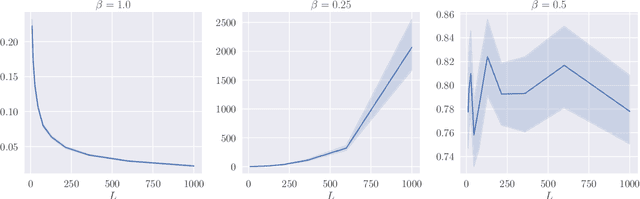
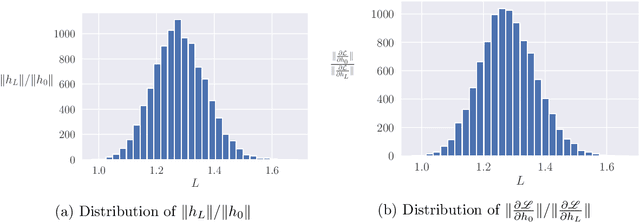
Deep ResNets are recognized for achieving state-of-the-art results in complex machine learning tasks. However, the remarkable performance of these architectures relies on a training procedure that needs to be carefully crafted to avoid vanishing or exploding gradients, particularly as the depth $L$ increases. No consensus has been reached on how to mitigate this issue, although a widely discussed strategy consists in scaling the output of each layer by a factor $\alpha_L$. We show in a probabilistic setting that with standard i.i.d. initializations, the only non-trivial dynamics is for $\alpha_L = 1/\sqrt{L}$ (other choices lead either to explosion or to identity mapping). This scaling factor corresponds in the continuous-time limit to a neural stochastic differential equation, contrarily to a widespread interpretation that deep ResNets are discretizations of neural ordinary differential equations. By contrast, in the latter regime, stability is obtained with specific correlated initializations and $\alpha_L = 1/L$. Our analysis suggests a strong interplay between scaling and regularity of the weights as a function of the layer index. Finally, in a series of experiments, we exhibit a continuous range of regimes driven by these two parameters, which jointly impact performance before and after training.

Framing RNN as a kernel method: A neural ODE approach

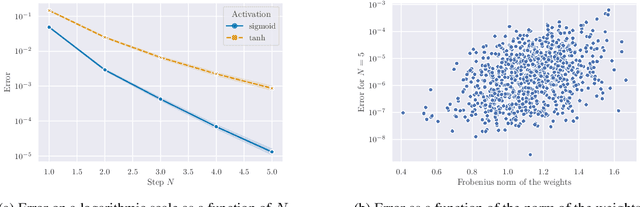
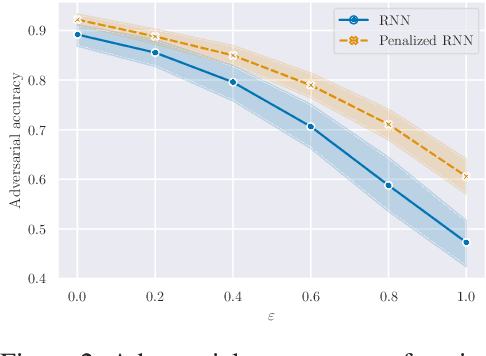
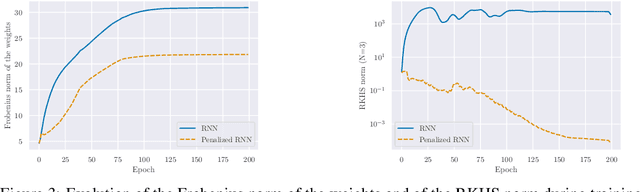
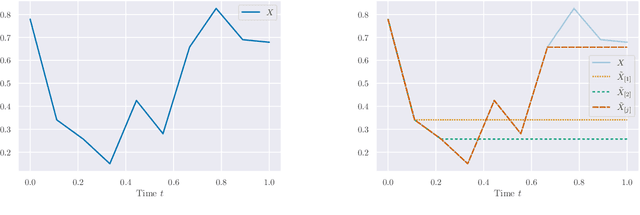
Building on the interpretation of a recurrent neural network (RNN) as a continuous-time neural differential equation, we show, under appropriate conditions, that the solution of a RNN can be viewed as a linear function of a specific feature set of the input sequence, known as the signature. This connection allows us to frame a RNN as a kernel method in a suitable reproducing kernel Hilbert space. As a consequence, we obtain theoretical guarantees on generalization and stability for a large class of recurrent networks. Our results are illustrated on simulated datasets.

A Generalised Signature Method for Time Series

The `signature method' refers to a collection of feature extraction techniques for multimodal sequential data, derived from the theory of controlled differential equations. Variations exist as many authors have proposed modifications to the method, so as to improve some aspect of it. Here, we introduce a \emph{generalised signature method} that contains these variations as special cases, and groups them conceptually into \emph{augmentations}, \emph{windows}, \emph{transforms}, and \emph{rescalings}. Within this framework we are then able to propose novel variations, and demonstrate how previously distinct options may be combined. We go on to perform an extensive empirical study on 26 datasets as to which aspects of this framework typically produce the best results. Combining the top choices produces a canonical pipeline for the generalised signature method, which demonstrates state-of-the-art accuracy on benchmark problems in multivariate time series classification.

Embedding and learning with signatures

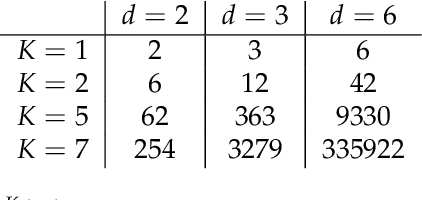
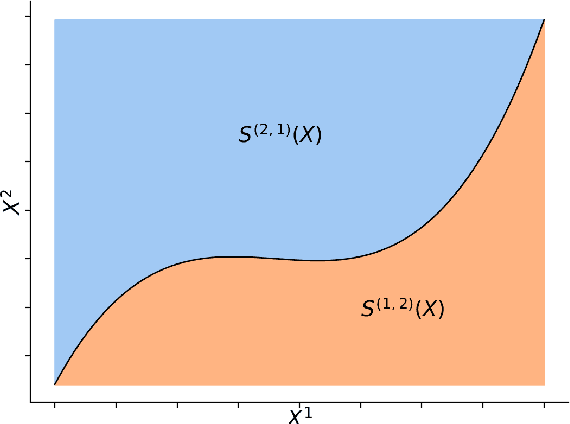
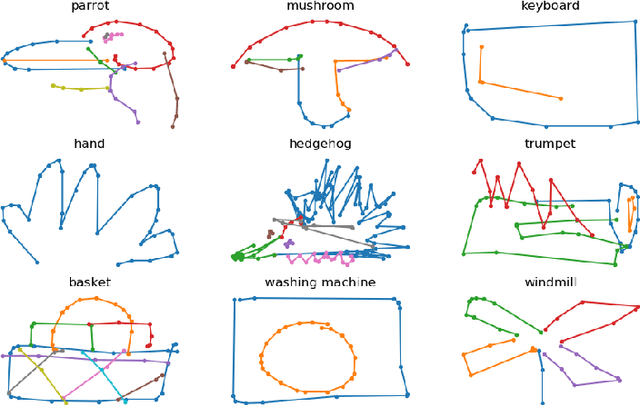
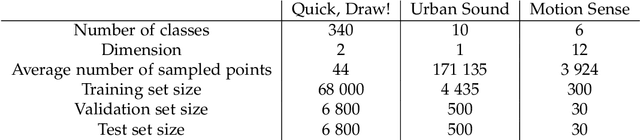
Sequential and temporal data arise in many fields of research, such as quantitative finance, medicine, or computer vision. The present article is concerned with a novel approach for sequential learning, called the signature method, and rooted in rough path theory. Its basic principle is to represent multidimensional paths by a graded feature set of their iterated integrals, called the signature. This approach relies critically on an embedding principle, which consists in representing discretely sampled data as paths, i.e., functions from $[0,1]$ to $R^d$. After a survey of machine learning methodologies for signatures, we investigate the influence of embeddings on prediction accuracy with an in-depth study of three recent and challenging datasets. We show that a specific embedding, called lead-lag, is systematically better, whatever the dataset or algorithm used. Moreover, we emphasize through an empirical study that computing signatures over the whole path domain does not lead to a loss of local information. We conclude that, with a good embedding, the signature combined with a simple algorithm achieves results competitive with state-of-the-art, domain-specific approaches.