Taking a Big Step: Large Learning Rates in Denoising Score Matching Prevent Memorization

Denoising score matching plays a pivotal role in the performance of diffusion-based generative models. However, the empirical optimal score--the exact solution to the denoising score matching--leads to memorization, where generated samples replicate the training data. Yet, in practice, only a moderate degree of memorization is observed, even without explicit regularization. In this paper, we investigate this phenomenon by uncovering an implicit regularization mechanism driven by large learning rates. Specifically, we show that in the small-noise regime, the empirical optimal score exhibits high irregularity. We then prove that, when trained by stochastic gradient descent with a large enough learning rate, neural networks cannot stably converge to a local minimum with arbitrarily small excess risk. Consequently, the learned score cannot be arbitrarily close to the empirical optimal score, thereby mitigating memorization. To make the analysis tractable, we consider one-dimensional data and two-layer neural networks. Experiments validate the crucial role of the learning rate in preventing memorization, even beyond the one-dimensional setting.

Attention layers provably solve single-location regression

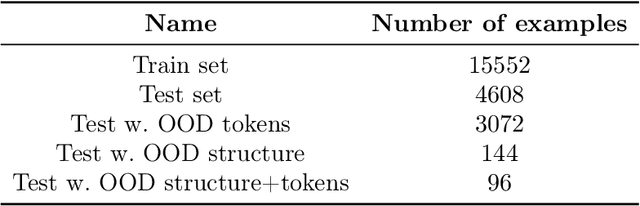
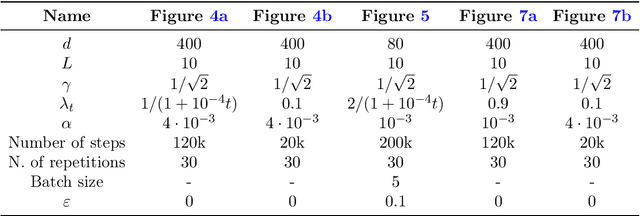
Attention-based models, such as Transformer, excel across various tasks but lack a comprehensive theoretical understanding, especially regarding token-wise sparsity and internal linear representations. To address this gap, we introduce the single-location regression task, where only one token in a sequence determines the output, and its position is a latent random variable, retrievable via a linear projection of the input. To solve this task, we propose a dedicated predictor, which turns out to be a simplified version of a non-linear self-attention layer. We study its theoretical properties, by showing its asymptotic Bayes optimality and analyzing its training dynamics. In particular, despite the non-convex nature of the problem, the predictor effectively learns the underlying structure. This work highlights the capacity of attention mechanisms to handle sparse token information and internal linear structures.

Physics-informed machine learning as a kernel method

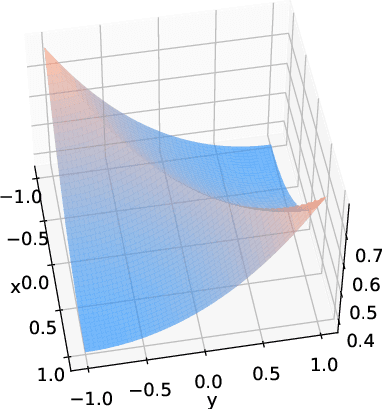
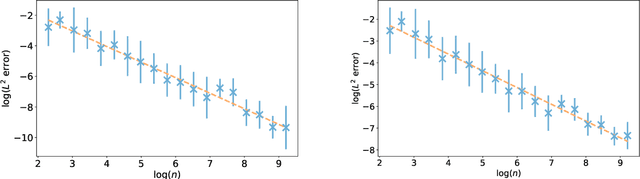
Physics-informed machine learning combines the expressiveness of data-based approaches with the interpretability of physical models. In this context, we consider a general regression problem where the empirical risk is regularized by a partial differential equation that quantifies the physical inconsistency. We prove that for linear differential priors, the problem can be formulated as a kernel regression task. Taking advantage of kernel theory, we derive convergence rates for the minimizer of the regularized risk and show that it converges at least at the Sobolev minimax rate. However, faster rates can be achieved, depending on the physical error. This principle is illustrated with a one-dimensional example, supporting the claim that regularizing the empirical risk with physical information can be beneficial to the statistical performance of estimators.

Implicit regularization of deep residual networks towards neural ODEs

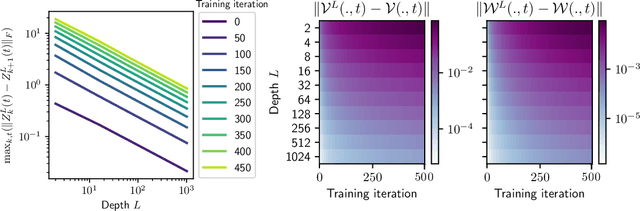
Residual neural networks are state-of-the-art deep learning models. Their continuous-depth analog, neural ordinary differential equations (ODEs), are also widely used. Despite their success, the link between the discrete and continuous models still lacks a solid mathematical foundation. In this article, we take a step in this direction by establishing an implicit regularization of deep residual networks towards neural ODEs, for nonlinear networks trained with gradient flow. We prove that if the network is initialized as a discretization of a neural ODE, then such a discretization holds throughout training. Our results are valid for a finite training time, and also as the training time tends to infinity provided that the network satisfies a Polyak-Lojasiewicz condition. Importantly, this condition holds for a family of residual networks where the residuals are two-layer perceptrons with an overparameterization in width that is only linear, and implies the convergence of gradient flow to a global minimum. Numerical experiments illustrate our results.

Scaling ResNets in the Large-depth Regime

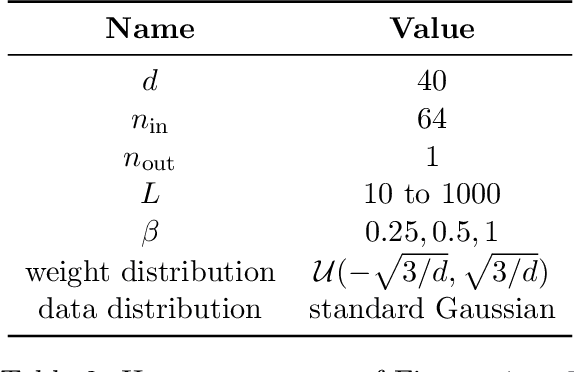
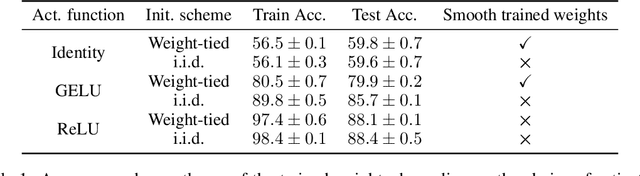
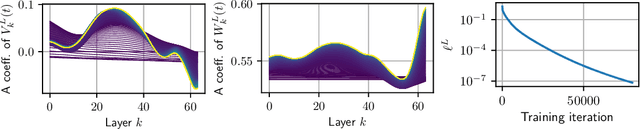
Deep ResNets are recognized for achieving state-of-the-art results in complex machine learning tasks. However, the remarkable performance of these architectures relies on a training procedure that needs to be carefully crafted to avoid vanishing or exploding gradients, particularly as the depth $L$ increases. No consensus has been reached on how to mitigate this issue, although a widely discussed strategy consists in scaling the output of each layer by a factor $\alpha_L$. We show in a probabilistic setting that with standard i.i.d. initializations, the only non-trivial dynamics is for $\alpha_L = 1/\sqrt{L}$ (other choices lead either to explosion or to identity mapping). This scaling factor corresponds in the continuous-time limit to a neural stochastic differential equation, contrarily to a widespread interpretation that deep ResNets are discretizations of neural ordinary differential equations. By contrast, in the latter regime, stability is obtained with specific correlated initializations and $\alpha_L = 1/L$. Our analysis suggests a strong interplay between scaling and regularity of the weights as a function of the layer index. Finally, in a series of experiments, we exhibit a continuous range of regimes driven by these two parameters, which jointly impact performance before and after training.

Optimal 1-Wasserstein Distance for WGANs

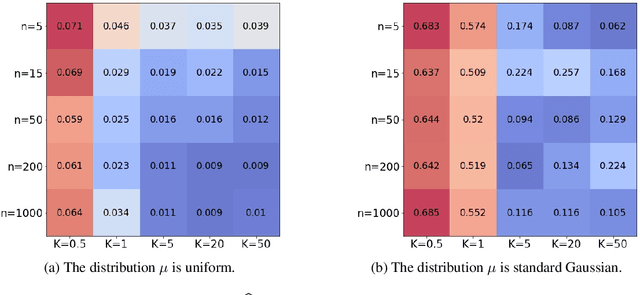
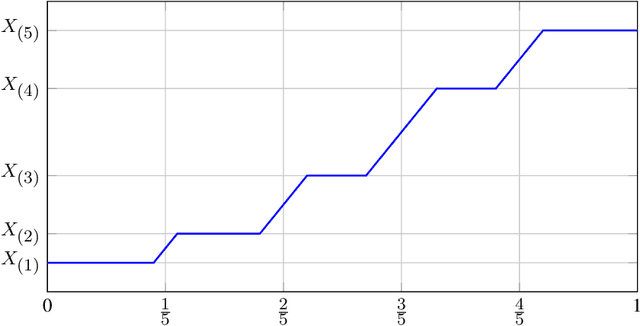
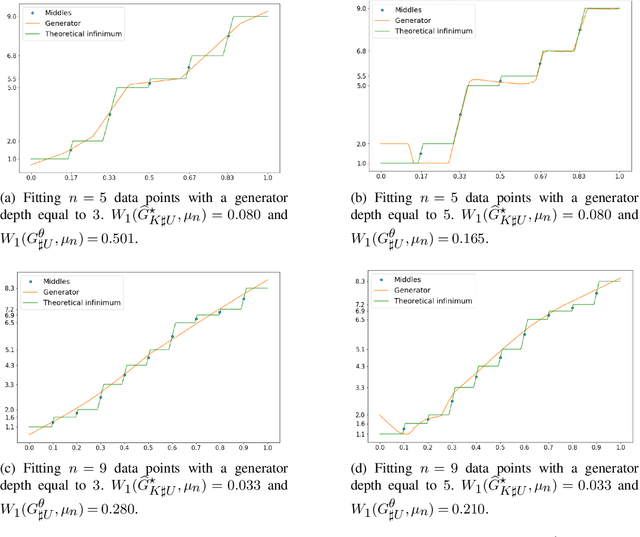
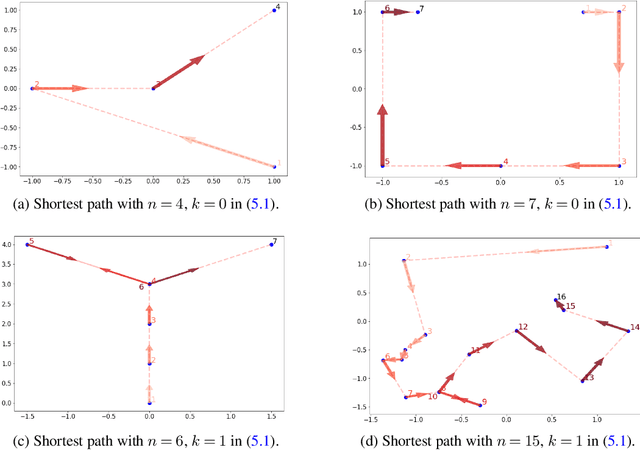
The mathematical forces at work behind Generative Adversarial Networks raise challenging theoretical issues. Motivated by the important question of characterizing the geometrical properties of the generated distributions, we provide a thorough analysis of Wasserstein GANs (WGANs) in both the finite sample and asymptotic regimes. We study the specific case where the latent space is univariate and derive results valid regardless of the dimension of the output space. We show in particular that for a fixed sample size, the optimal WGANs are closely linked with connected paths minimizing the sum of the squared Euclidean distances between the sample points. We also highlight the fact that WGANs are able to approach (for the 1-Wasserstein distance) the target distribution as the sample size tends to infinity, at a given convergence rate and provided the family of generative Lipschitz functions grows appropriately. We derive in passing new results on optimal transport theory in the semi-discrete setting.

Framing RNN as a kernel method: A neural ODE approach

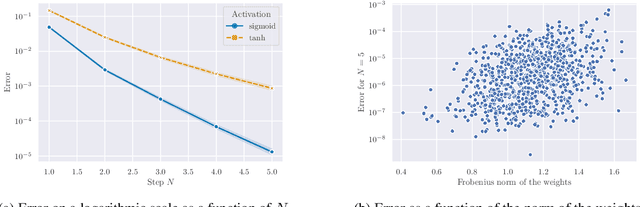
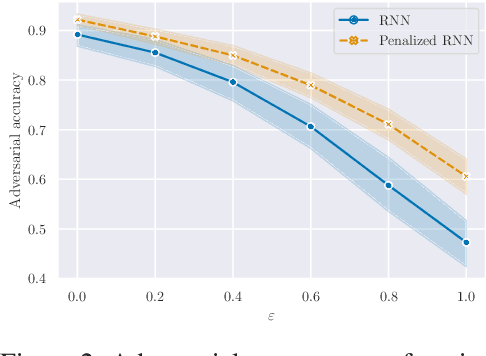
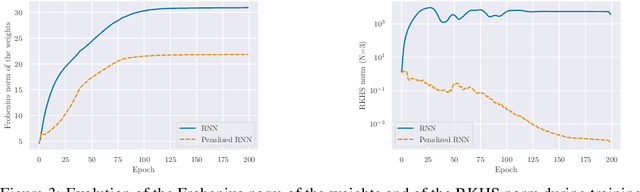
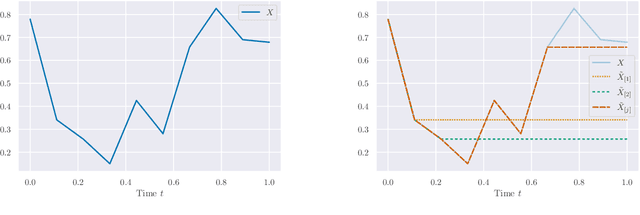
Building on the interpretation of a recurrent neural network (RNN) as a continuous-time neural differential equation, we show, under appropriate conditions, that the solution of a RNN can be viewed as a linear function of a specific feature set of the input sequence, known as the signature. This connection allows us to frame a RNN as a kernel method in a suitable reproducing kernel Hilbert space. As a consequence, we obtain theoretical guarantees on generalization and stability for a large class of recurrent networks. Our results are illustrated on simulated datasets.

SHAFF: Fast and consistent SHApley eFfect estimates via random Forests

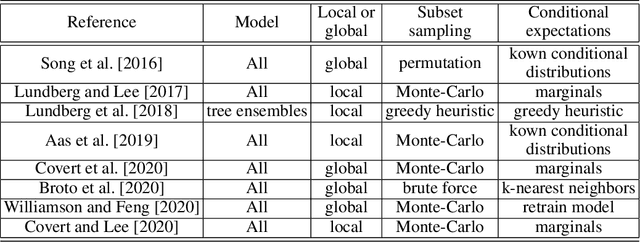
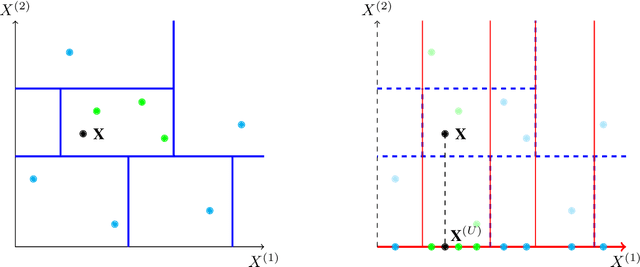
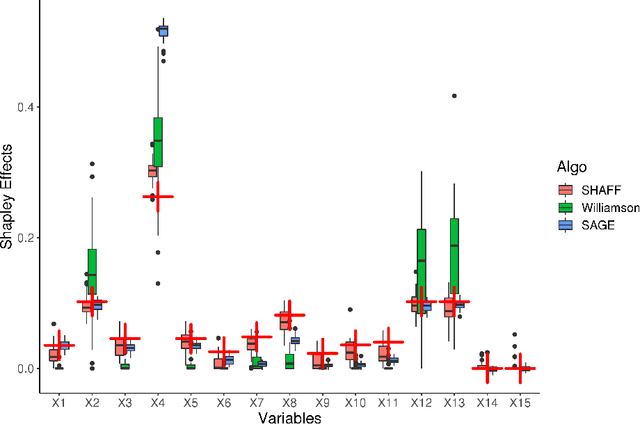
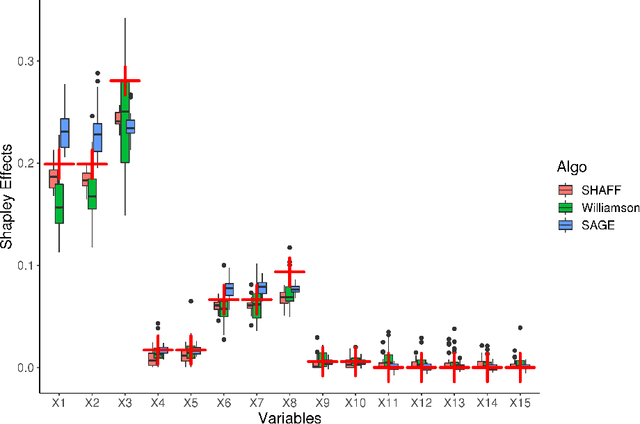
Interpretability of learning algorithms is crucial for applications involving critical decisions, and variable importance is one of the main interpretation tools. Shapley effects are now widely used to interpret both tree ensembles and neural networks, as they can efficiently handle dependence and interactions in the data, as opposed to most other variable importance measures. However, estimating Shapley effects is a challenging task, because of the computational complexity and the conditional expectation estimates. Accordingly, existing Shapley algorithms have flaws: a costly running time, or a bias when input variables are dependent. Therefore, we introduce SHAFF, SHApley eFfects via random Forests, a fast and accurate Shapley effect estimate, even when input variables are dependent. We show SHAFF efficiency through both a theoretical analysis of its consistency, and the practical performance improvements over competitors with extensive experiments. An implementation of SHAFF in C++ and R is available online.

Wasserstein Random Forests and Applications in Heterogeneous Treatment Effects

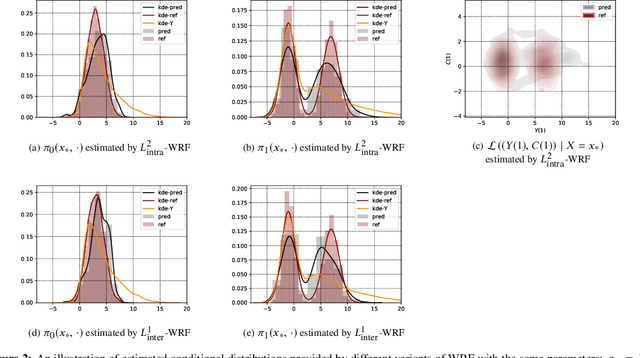
We present new insights into causal inference in the context of Heterogeneous Treatment Effects by proposing natural variants of Random Forests to estimate the key conditional distributions. To achieve this, we recast Breiman's original splitting criterion in terms of Wasserstein distances between empirical measures. This reformulation indicates that Random Forests are well adapted to estimate conditional distributions and provides a natural extension of the algorithm to multivariate outputs. Following the philosophy of Breiman's construction, we propose some variants of the splitting rule that are well-suited to the conditional distribution estimation problem. Some preliminary theoretical connections are established along with various numerical experiments, which show how our approach may help to conduct more transparent causal inference in complex situations.

Some Theoretical Insights into Wasserstein GANs

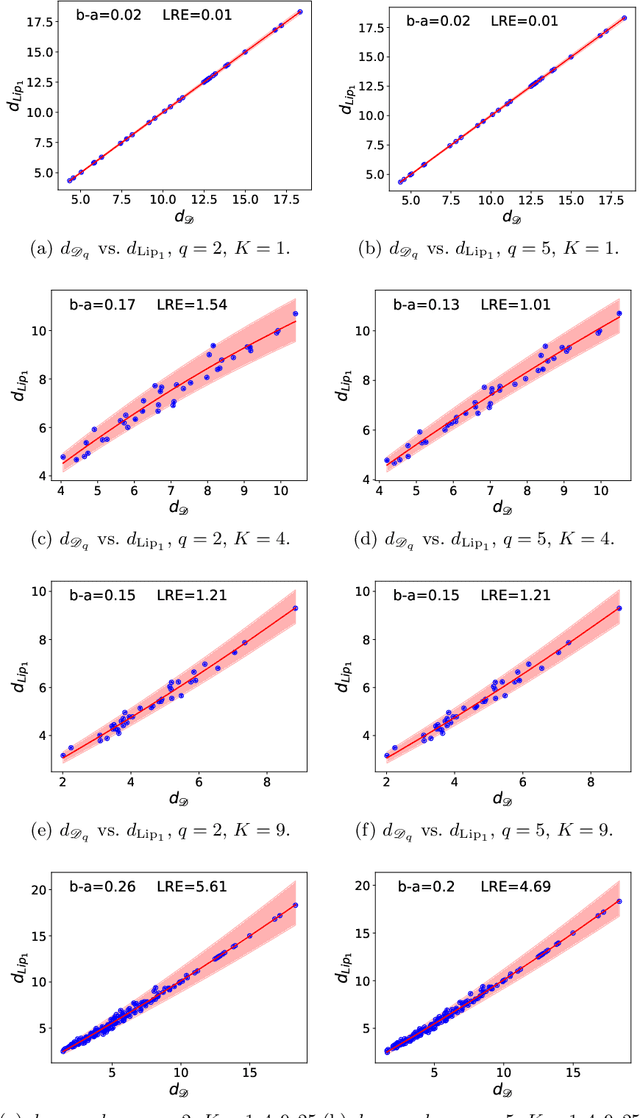
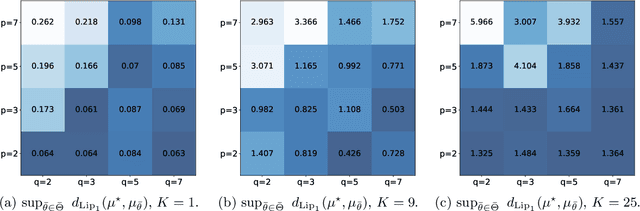
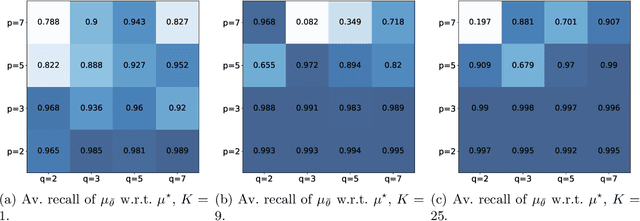
Generative Adversarial Networks (GANs) have been successful in producing outstanding results in areas as diverse as image, video, and text generation. Building on these successes, a large number of empirical studies have validated the benefits of the cousin approach called Wasserstein GANs (WGANs), which brings stabilization in the training process. In the present paper, we add a new stone to the edifice by proposing some theoretical advances in the properties of WGANs. First, we properly define the architecture of WGANs in the context of integral probability metrics parameterized by neural networks and highlight some of their basic mathematical features. We stress in particular interesting optimization properties arising from the use of a parametric 1-Lipschitz discriminator. Then, in a statistically-driven approach, we study the convergence of empirical WGANs as the sample size tends to infinity, and clarify the adversarial effects of the generator and the discrimi-nator by underlining some trade-off properties. These features are finally illustrated with experiments using both synthetic and real-world datasets.