Optimal 1-Wasserstein Distance for WGANs

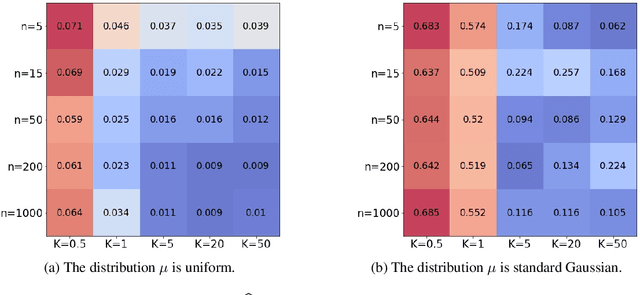
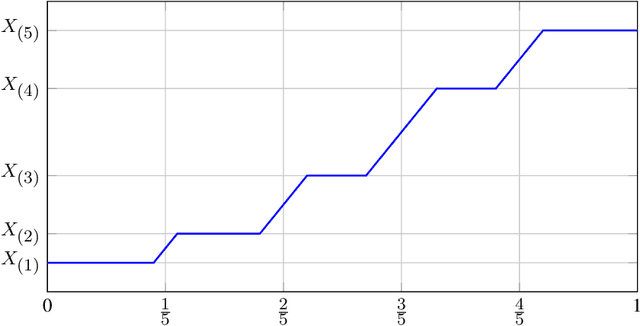
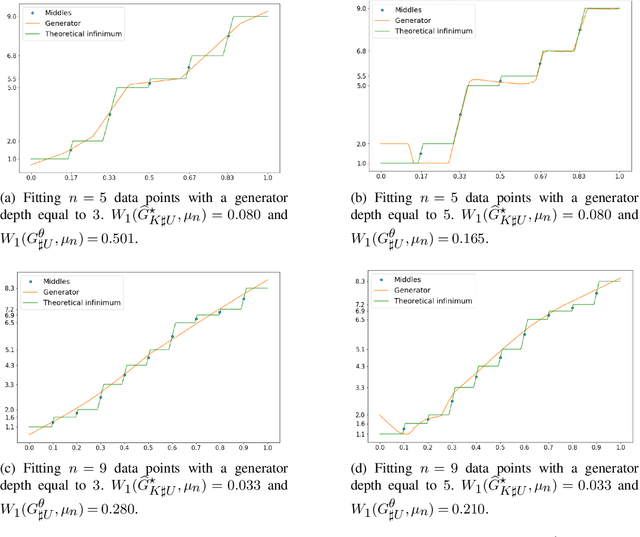
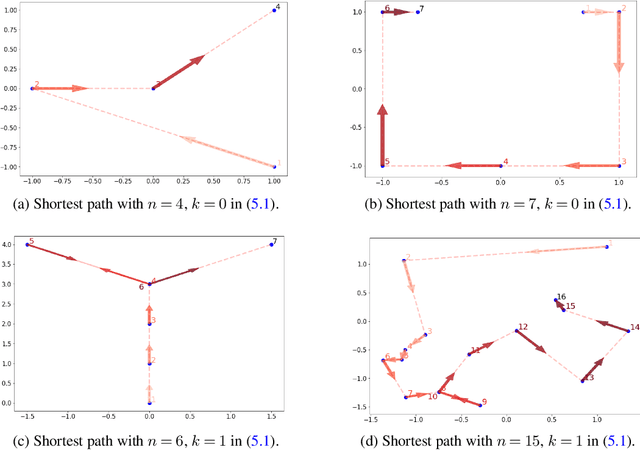
The mathematical forces at work behind Generative Adversarial Networks raise challenging theoretical issues. Motivated by the important question of characterizing the geometrical properties of the generated distributions, we provide a thorough analysis of Wasserstein GANs (WGANs) in both the finite sample and asymptotic regimes. We study the specific case where the latent space is univariate and derive results valid regardless of the dimension of the output space. We show in particular that for a fixed sample size, the optimal WGANs are closely linked with connected paths minimizing the sum of the squared Euclidean distances between the sample points. We also highlight the fact that WGANs are able to approach (for the 1-Wasserstein distance) the target distribution as the sample size tends to infinity, at a given convergence rate and provided the family of generative Lipschitz functions grows appropriately. We derive in passing new results on optimal transport theory in the semi-discrete setting.

Clustering multivariate functional data using unsupervised binary trees

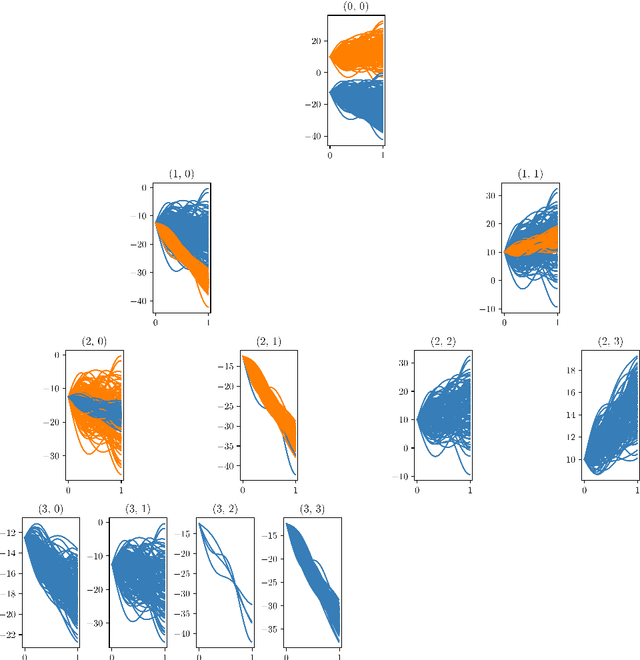
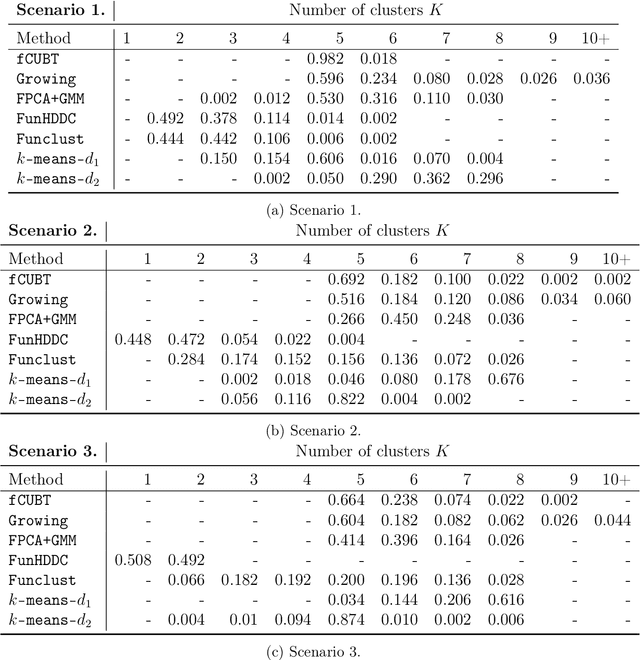
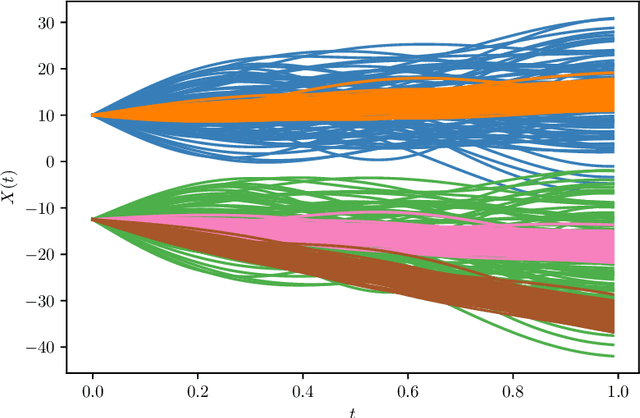
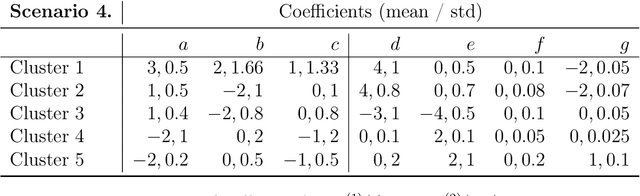
We propose a model-based clustering algorithm for a general class of functional data for which the components could be curves or images. The random functional data realizations could be measured with error at discrete, and possibly random, points in the definition domain. The idea is to build a set of binary trees by recursive splitting of the observations. The number of groups are determined in a data-driven way. The new algorithm provides easily interpretable results and fast predictions for online data sets. Results on simulated datasets reveal good performance in various complex settings. The methodology is applied to the analysis of vehicle trajectories on a German roundabout.