On the estimation of the number of components in multivariate functional principal component analysis

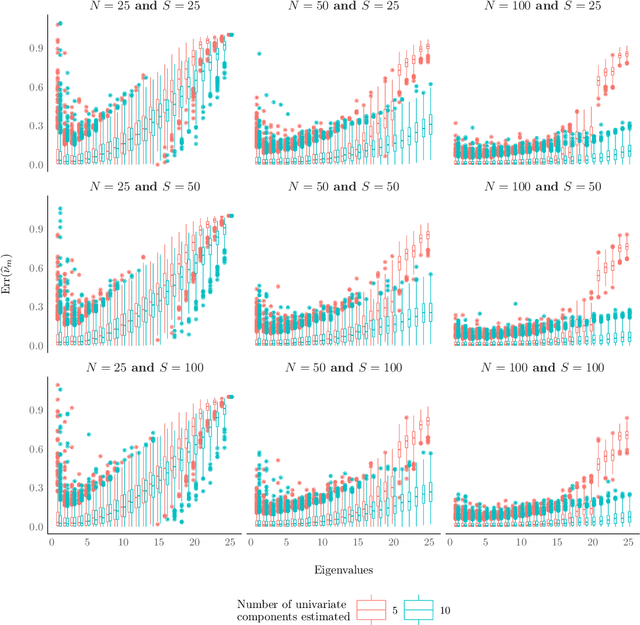
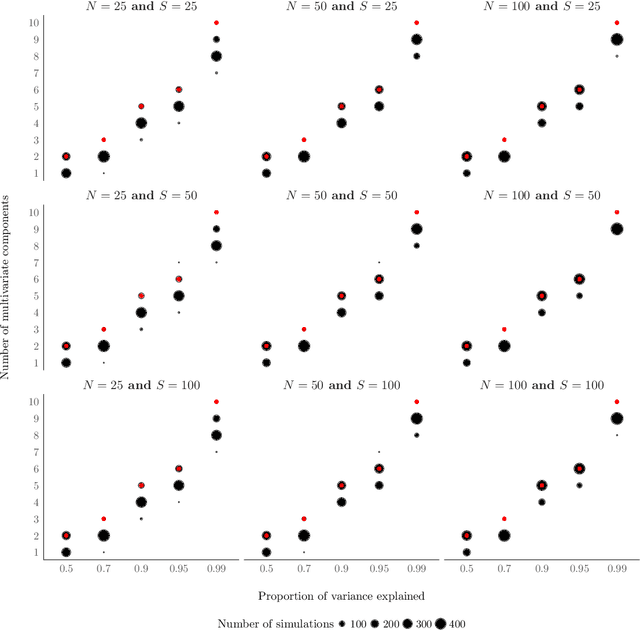
Happ and Greven (2018) developed a methodology for principal components analysis of multivariate functional data for data observed on different dimensional domains. Their approach relies on an estimation of univariate functional principal components for each univariate functional feature. In this paper, we present extensive simulations to investigate choosing the number of principal components to retain. We show empirically that the conventional approach of using a percentage of variance explained threshold for each univariate functional feature may be unreliable when aiming to explain an overall percentage of variance in the multivariate functional data, and thus we advise practitioners to be careful when using it.

On the use of the Gram matrix for multivariate functional principal components analysis

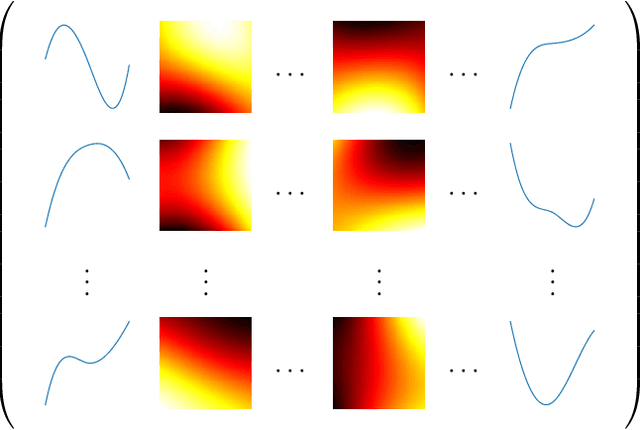
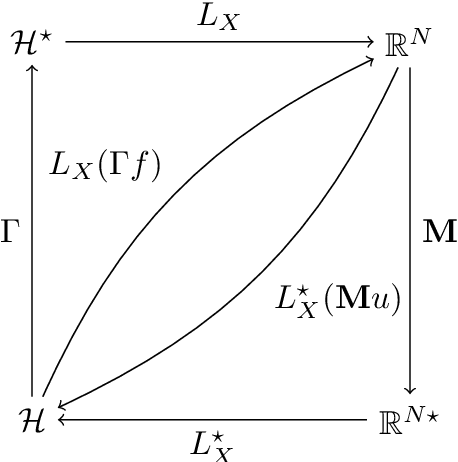
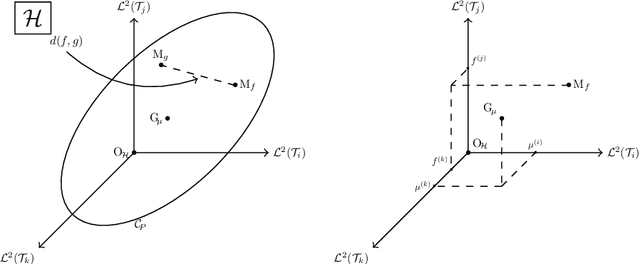
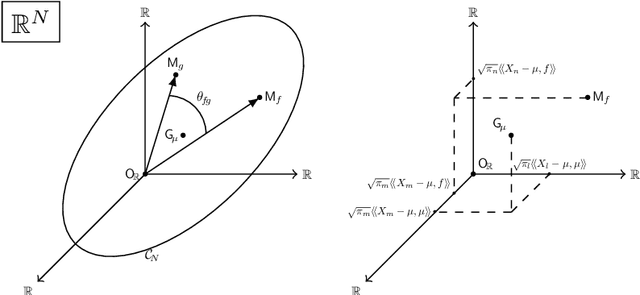
Dimension reduction is crucial in functional data analysis (FDA). The key tool to reduce the dimension of the data is functional principal component analysis. Existing approaches for functional principal component analysis usually involve the diagonalization of the covariance operator. With the increasing size and complexity of functional datasets, estimating the covariance operator has become more challenging. Therefore, there is a growing need for efficient methodologies to estimate the eigencomponents. Using the duality of the space of observations and the space of functional features, we propose to use the inner-product between the curves to estimate the eigenelements of multivariate and multidimensional functional datasets. The relationship between the eigenelements of the covariance operator and those of the inner-product matrix is established. We explore the application of these methodologies in several FDA settings and provide general guidance on their usability.

FDApy: a Python package for functional data

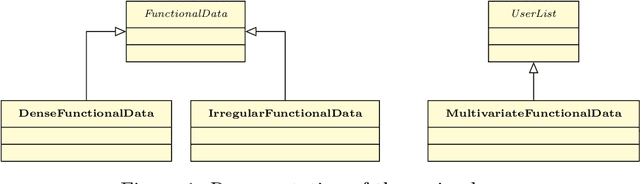
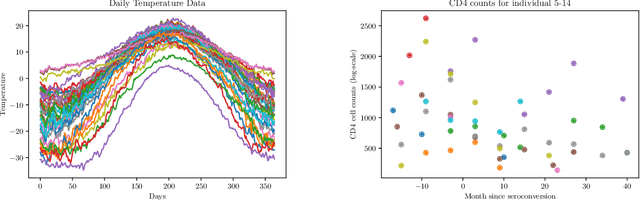
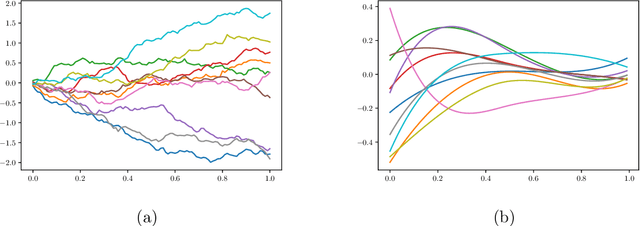
We introduce the Python package, FDApy, as an implementation of functional data. This package provide modules for the analysis of such data. It includes classes for different dimensional data as well as irregularly sampled functional data. A simulation toolbox is also provided. It might be used to simulate different clusters of functional data. Some methodologies to handle these data are implemented, such as dimension reduction and clustering. New methods can be easily added. The package is publicly available on the Python Package Index and Github.

Clustering multivariate functional data using unsupervised binary trees

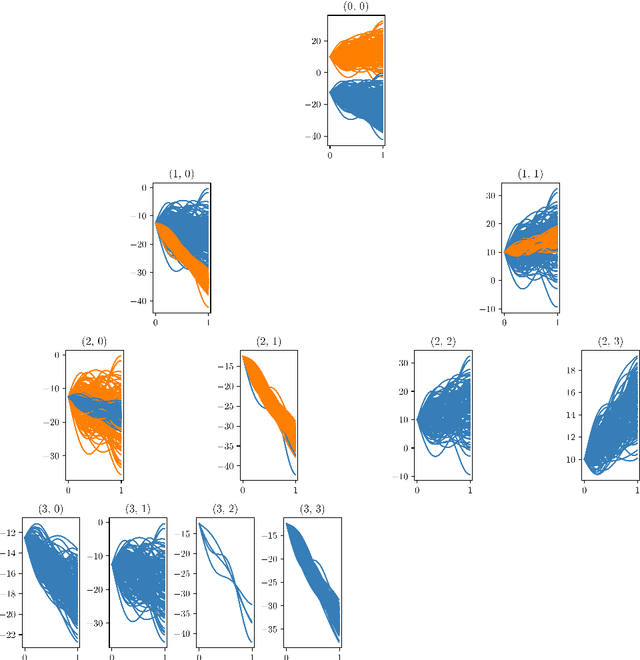
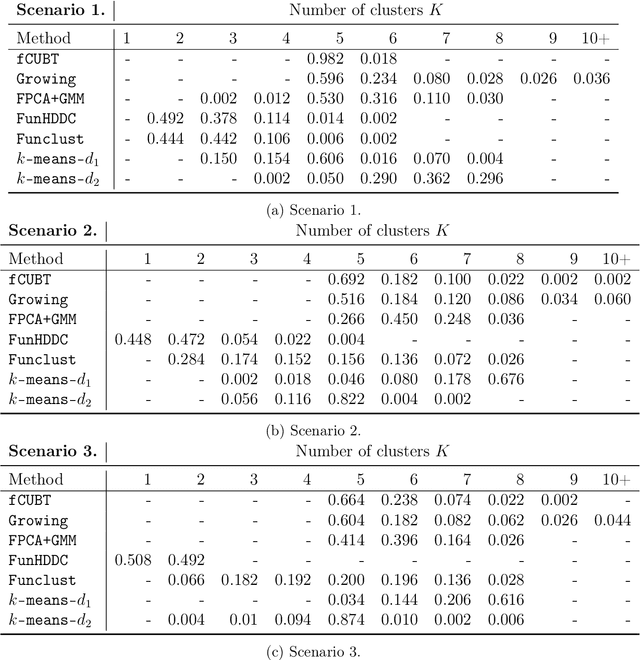
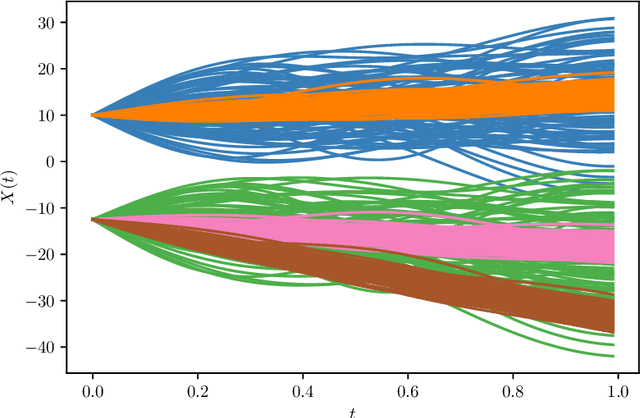
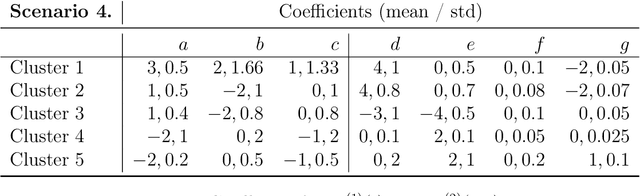
We propose a model-based clustering algorithm for a general class of functional data for which the components could be curves or images. The random functional data realizations could be measured with error at discrete, and possibly random, points in the definition domain. The idea is to build a set of binary trees by recursive splitting of the observations. The number of groups are determined in a data-driven way. The new algorithm provides easily interpretable results and fast predictions for online data sets. Results on simulated datasets reveal good performance in various complex settings. The methodology is applied to the analysis of vehicle trajectories on a German roundabout.