Optimal 1-Wasserstein Distance for WGANs

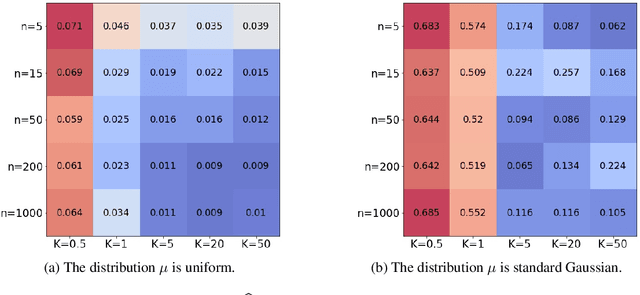
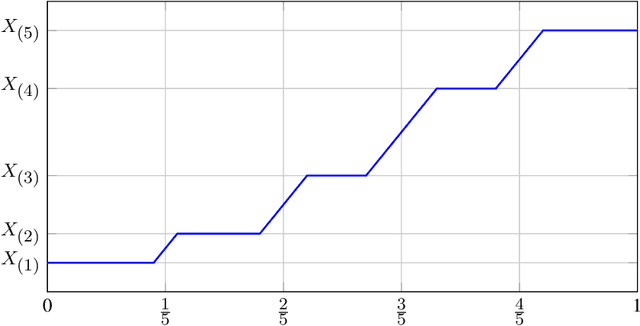
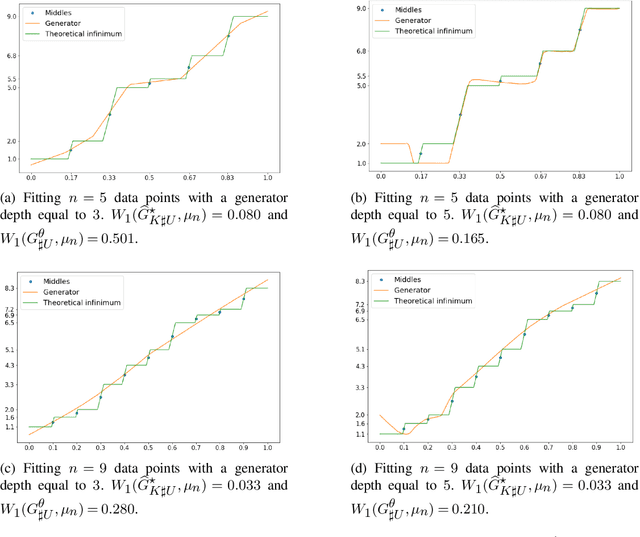
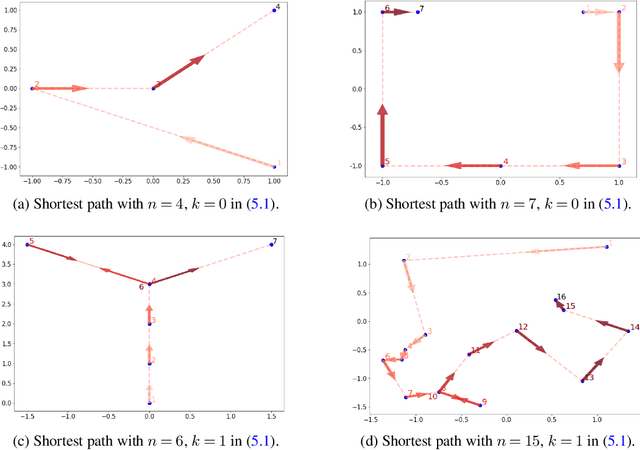
The mathematical forces at work behind Generative Adversarial Networks raise challenging theoretical issues. Motivated by the important question of characterizing the geometrical properties of the generated distributions, we provide a thorough analysis of Wasserstein GANs (WGANs) in both the finite sample and asymptotic regimes. We study the specific case where the latent space is univariate and derive results valid regardless of the dimension of the output space. We show in particular that for a fixed sample size, the optimal WGANs are closely linked with connected paths minimizing the sum of the squared Euclidean distances between the sample points. We also highlight the fact that WGANs are able to approach (for the 1-Wasserstein distance) the target distribution as the sample size tends to infinity, at a given convergence rate and provided the family of generative Lipschitz functions grows appropriately. We derive in passing new results on optimal transport theory in the semi-discrete setting.

Accelerated Gradient Boosting

Gradient tree boosting is a prediction algorithm that sequentially produces a model in the form of linear combinations of decision trees, by solving an infinite-dimensional optimization problem. We combine gradient boosting and Nesterov's accelerated descent to design a new algorithm, which we call AGB (for Accelerated Gradient Boosting). Substantial numerical evidence is provided on both synthetic and real-life data sets to assess the excellent performance of the method in a large variety of prediction problems. It is empirically shown that AGB is much less sensitive to the shrinkage parameter and outputs predictors that are considerably more sparse in the number of trees, while retaining the exceptional performance of gradient boosting.

Optimization by gradient boosting

Gradient boosting is a state-of-the-art prediction technique that sequentially produces a model in the form of linear combinations of simple predictors---typically decision trees---by solving an infinite-dimensional convex optimization problem. We provide in the present paper a thorough analysis of two widespread versions of gradient boosting, and introduce a general framework for studying these algorithms from the point of view of functional optimization. We prove their convergence as the number of iterations tends to infinity and highlight the importance of having a strongly convex risk functional to minimize. We also present a reasonable statistical context ensuring consistency properties of the boosting predictors as the sample size grows. In our approach, the optimization procedures are run forever (that is, without resorting to an early stopping strategy), and statistical regularization is basically achieved via an appropriate $L^2$ penalization of the loss and strong convexity arguments.