Nonparametric estimation of Hawkes processes with RKHSs

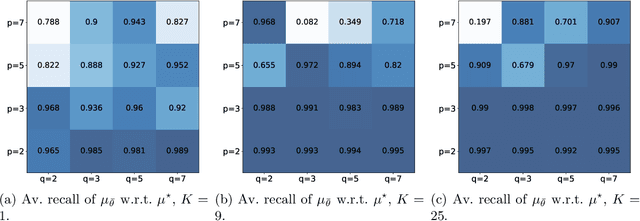
This paper addresses nonparametric estimation of nonlinear multivariate Hawkes processes, where the interaction functions are assumed to lie in a reproducing kernel Hilbert space (RKHS). Motivated by applications in neuroscience, the model allows complex interaction functions, in order to express exciting and inhibiting effects, but also a combination of both (which is particularly interesting to model the refractory period of neurons), and considers in return that conditional intensities are rectified by the ReLU function. The latter feature incurs several methodological challenges, for which workarounds are proposed in this paper. In particular, it is shown that a representer theorem can be obtained for approximated versions of the log-likelihood and the least-squares criteria. Based on it, we propose an estimation method, that relies on two simple approximations (of the ReLU function and of the integral operator). We provide an approximation bound, justifying the negligible statistical effect of these approximations. Numerical results on synthetic data confirm this fact as well as the good asymptotic behavior of the proposed estimator. It also shows that our method achieves a better performance compared to related nonparametric estimation techniques and suits neuronal applications.

Maximum Likelihood Estimation for Hawkes Processes with self-excitation or inhibition

In this paper, we present a maximum likelihood method for estimating the parameters of a univariate Hawkes process with self-excitation or inhibition. Our work generalizes techniques and results that were restricted to the self-exciting scenario. The proposed estimator is implemented for the classical exponential kernel and we show that, in the inhibition context, our procedure provides more accurate estimations than current alternative approaches.

Approximating Lipschitz continuous functions with GroupSort neural networks

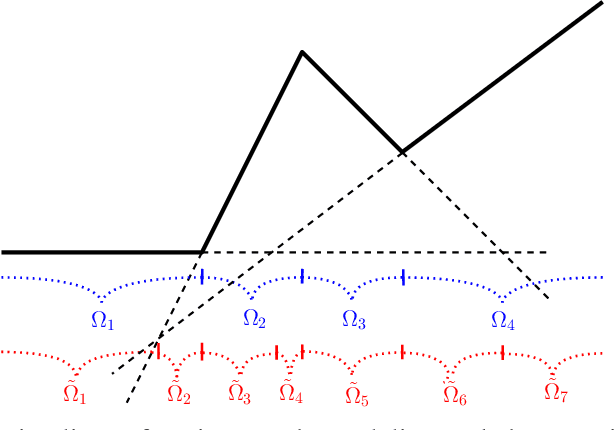
Recent advances in adversarial attacks and Wasserstein GANs have advocated for use of neural networks with restricted Lipschitz constants. Motivated by these observations, we study the recently introduced GroupSort neural networks, with constraints on the weights, and make a theoretical step towards a better understanding of their expressive power. We show in particular how these networks can represent any Lipschitz continuous piecewise linear functions. We also prove that they are well-suited for approximating Lipschitz continuous functions and exhibit upper bounds on both the depth and size. To conclude, the efficiency of GroupSort networks compared with more standard ReLU networks is illustrated in a set of synthetic experiments.

Some Theoretical Insights into Wasserstein GANs

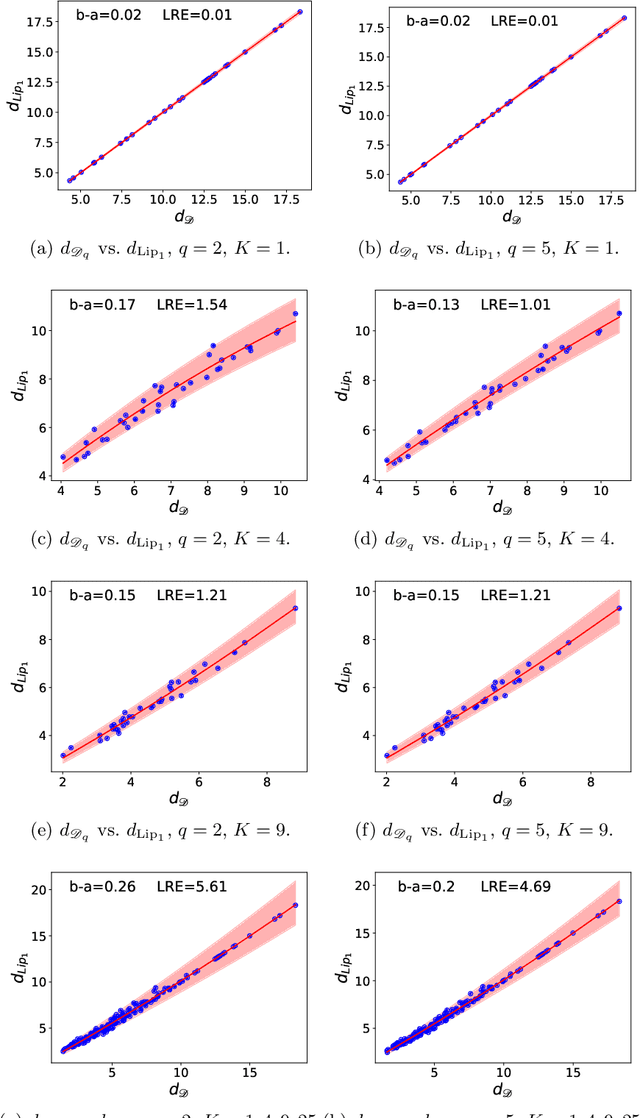
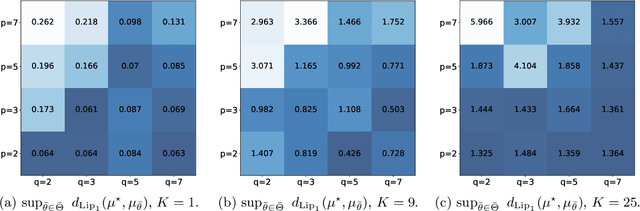
Generative Adversarial Networks (GANs) have been successful in producing outstanding results in areas as diverse as image, video, and text generation. Building on these successes, a large number of empirical studies have validated the benefits of the cousin approach called Wasserstein GANs (WGANs), which brings stabilization in the training process. In the present paper, we add a new stone to the edifice by proposing some theoretical advances in the properties of WGANs. First, we properly define the architecture of WGANs in the context of integral probability metrics parameterized by neural networks and highlight some of their basic mathematical features. We stress in particular interesting optimization properties arising from the use of a parametric 1-Lipschitz discriminator. Then, in a statistically-driven approach, we study the convergence of empirical WGANs as the sample size tends to infinity, and clarify the adversarial effects of the generator and the discrimi-nator by underlining some trade-off properties. These features are finally illustrated with experiments using both synthetic and real-world datasets.

Infinite-Task Learning with RKHSs

Machine learning has witnessed tremendous success in solving tasks depending on a single hyperparameter. When considering simultaneously a finite number of tasks, multi-task learning enables one to account for the similarities of the tasks via appropriate regularizers. A step further consists of learning a continuum of tasks for various loss functions. A promising approach, called \emph{Parametric Task Learning}, has paved the way in the continuum setting for affine models and piecewise-linear loss functions. In this work, we introduce a novel approach called \emph{Infinite Task Learning} whose goal is to learn a function whose output is a function over the hyperparameter space. We leverage tools from operator-valued kernels and the associated vector-valued RKHSs that provide an explicit control over the role of the hyperparameters, and also allows us to consider new type of constraints. We provide generalization guarantees to the suggested scheme and illustrate its efficiency in cost-sensitive classification, quantile regression and density level set estimation.

Accelerated proximal boosting

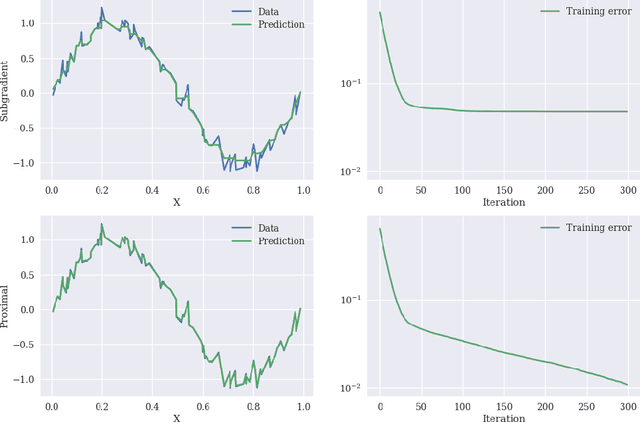
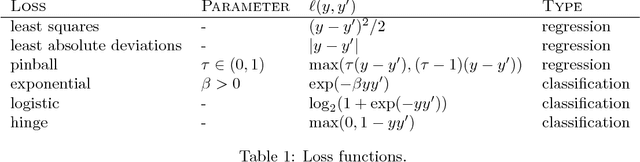
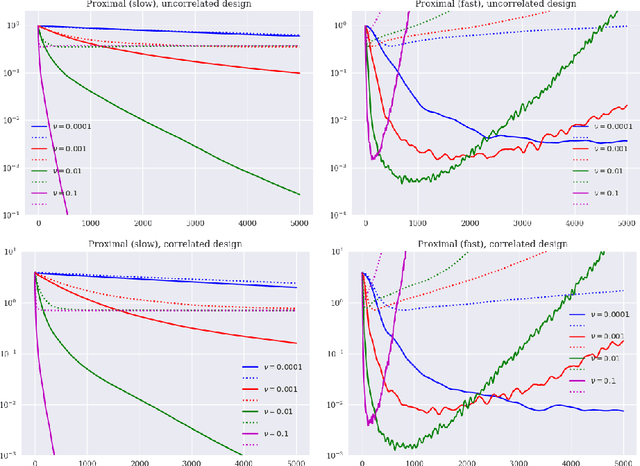
Gradient boosting is a prediction method that iteratively combines weak learners to produce a complex and accurate model. From an optimization point of view, the learning procedure of gradient boosting mimics a gradient descent on a functional variable. This paper proposes to build upon the proximal point algorithm when the empirical risk to minimize is not differentiable. In addition, the novel boosting approach, called accelerated proximal boosting, benefits from Nesterov's acceleration in the same way as gradient boosting [Biau et al., 2018]. Advantages of leveraging proximal methods for boosting are illustrated by numerical experiments on simulated and real-world data. In particular, we exhibit a favorable comparison over gradient boosting regarding convergence rate and prediction accuracy.