Erwan Fouillen
Accelerated proximal boosting
Aug 29, 2018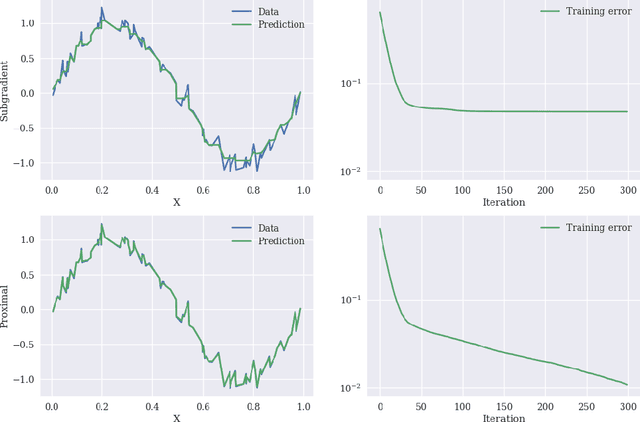
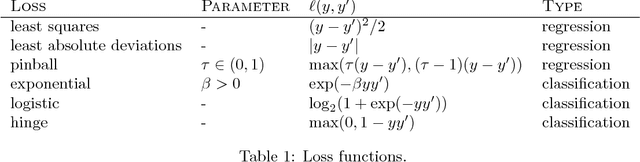
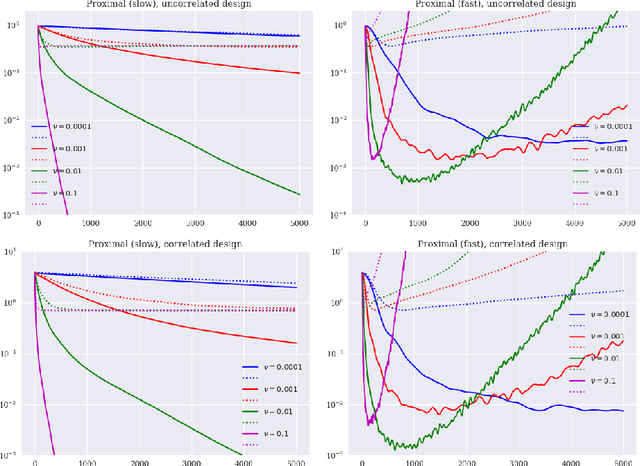

Abstract:Gradient boosting is a prediction method that iteratively combines weak learners to produce a complex and accurate model. From an optimization point of view, the learning procedure of gradient boosting mimics a gradient descent on a functional variable. This paper proposes to build upon the proximal point algorithm when the empirical risk to minimize is not differentiable. In addition, the novel boosting approach, called accelerated proximal boosting, benefits from Nesterov's acceleration in the same way as gradient boosting [Biau et al., 2018]. Advantages of leveraging proximal methods for boosting are illustrated by numerical experiments on simulated and real-world data. In particular, we exhibit a favorable comparison over gradient boosting regarding convergence rate and prediction accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge