Michael E. Sander
Autoregressive Language Models are Secretly Energy-Based Models: Insights into the Lookahead Capabilities of Next-Token Prediction
Dec 17, 2025Abstract:Autoregressive models (ARMs) currently constitute the dominant paradigm for large language models (LLMs). Energy-based models (EBMs) represent another class of models, which have historically been less prevalent in LLM development, yet naturally characterize the optimal policy in post-training alignment. In this paper, we provide a unified view of these two model classes. Taking the chain rule of probability as a starting point, we establish an explicit bijection between ARMs and EBMs in function space, which we show to correspond to a special case of the soft Bellman equation in maximum entropy reinforcement learning. Building upon this bijection, we derive the equivalence between supervised learning of ARMs and EBMs. Furthermore, we analyze the distillation of EBMs into ARMs by providing theoretical error bounds. Our results provide insights into the ability of ARMs to plan ahead, despite being based on the next-token prediction paradigm.
Joint Learning of Energy-based Models and their Partition Function
Jan 30, 2025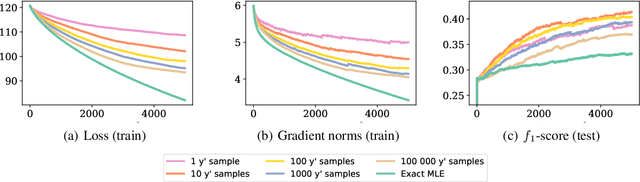
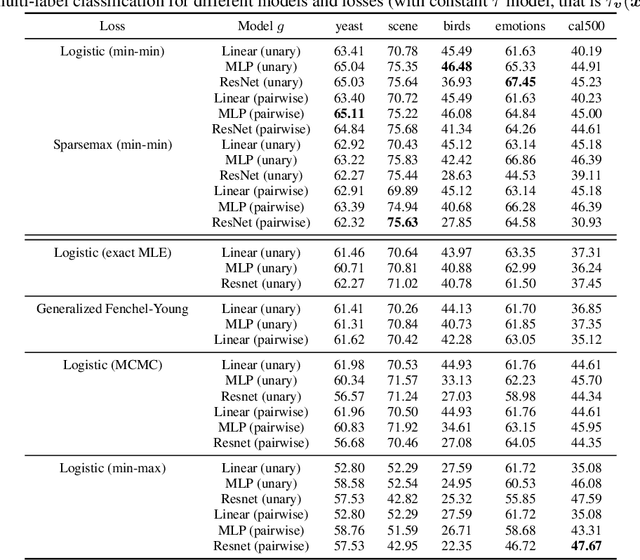
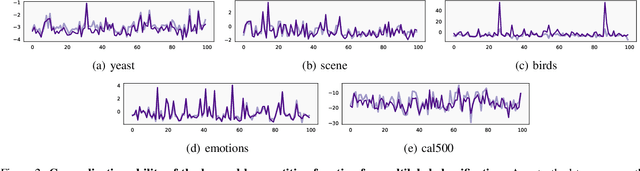
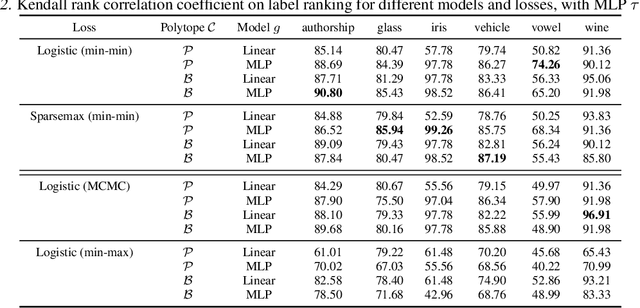
Abstract:Energy-based models (EBMs) offer a flexible framework for parameterizing probability distributions using neural networks. However, learning EBMs by exact maximum likelihood estimation (MLE) is generally intractable, due to the need to compute the partition function (normalization constant). In this paper, we propose a novel formulation for approximately learning probabilistic EBMs in combinatorially-large discrete spaces, such as sets or permutations. Our key idea is to jointly learn both an energy model and its log-partition, both parameterized as a neural network. Our approach not only provides a novel tractable objective criterion to learn EBMs by stochastic gradient descent (without relying on MCMC), but also a novel means to estimate the log-partition function on unseen data points. On the theoretical side, we show that our approach recovers the optimal MLE solution when optimizing in the space of continuous functions. Furthermore, we show that our approach naturally extends to the broader family of Fenchel-Young losses, allowing us to obtain the first tractable method for optimizing the sparsemax loss in combinatorially-large spaces. We demonstrate our approach on multilabel classification and label ranking.
Loss Functions and Operators Generated by f-Divergences
Jan 30, 2025Abstract:The logistic loss (a.k.a. cross-entropy loss) is one of the most popular loss functions used for multiclass classification. It is also the loss function of choice for next-token prediction in language modeling. It is associated with the Kullback--Leibler (KL) divergence and the softargmax operator. In this work, we propose to construct new convex loss functions based on $f$-divergences. Our loss functions generalize the logistic loss in two directions: i) by replacing the KL divergence with $f$-divergences and ii) by allowing non-uniform reference measures. We instantiate our framework for numerous $f$-divergences, recovering existing losses and creating new ones. By analogy with the logistic loss, the loss function generated by an $f$-divergence is associated with an operator, that we dub $f$-softargmax. We derive a novel parallelizable bisection algorithm for computing the $f$-softargmax associated with any $f$-divergence. On the empirical side, one of the goals of this paper is to determine the effectiveness of loss functions beyond the classical cross-entropy in a language model setting, including on pre-training, post-training (SFT) and distillation. We show that the loss function generated by the $\alpha$-divergence (which is equivalent to Tsallis $\alpha$-negentropy in the case of unit reference measures) with $\alpha=1.5$ performs well across several tasks.
Towards Understanding the Universality of Transformers for Next-Token Prediction
Oct 03, 2024
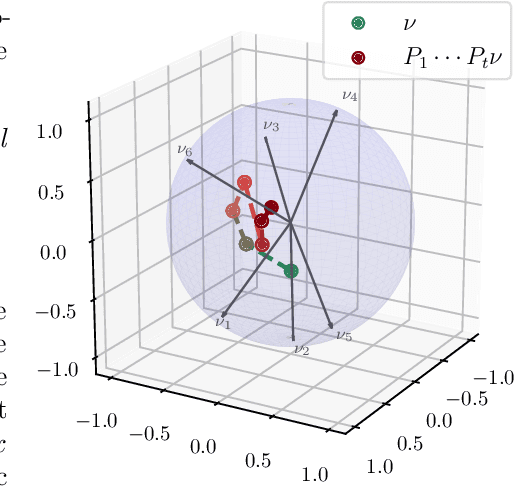

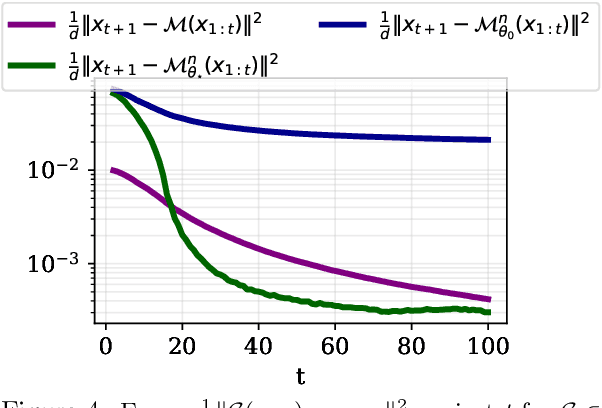
Abstract:Causal Transformers are trained to predict the next token for a given context. While it is widely accepted that self-attention is crucial for encoding the causal structure of sequences, the precise underlying mechanism behind this in-context autoregressive learning ability remains unclear. In this paper, we take a step towards understanding this phenomenon by studying the approximation ability of Transformers for next-token prediction. Specifically, we explore the capacity of causal Transformers to predict the next token $x_{t+1}$ given an autoregressive sequence $(x_1, \dots, x_t)$ as a prompt, where $ x_{t+1} = f(x_t) $, and $ f $ is a context-dependent function that varies with each sequence. On the theoretical side, we focus on specific instances, namely when $ f $ is linear or when $ (x_t)_{t \geq 1} $ is periodic. We explicitly construct a Transformer (with linear, exponential, or softmax attention) that learns the mapping $f$ in-context through a causal kernel descent method. The causal kernel descent method we propose provably estimates $x_{t+1} $ based solely on past and current observations $ (x_1, \dots, x_t) $, with connections to the Kaczmarz algorithm in Hilbert spaces. We present experimental results that validate our theoretical findings and suggest their applicability to more general mappings $f$.
How do Transformers perform In-Context Autoregressive Learning?
Feb 08, 2024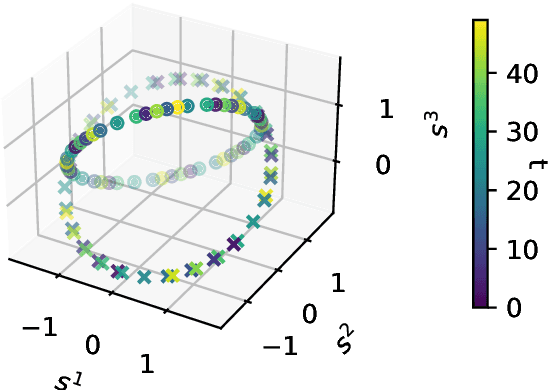
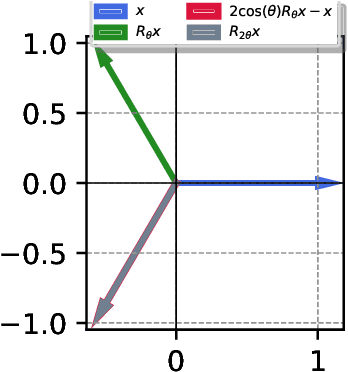

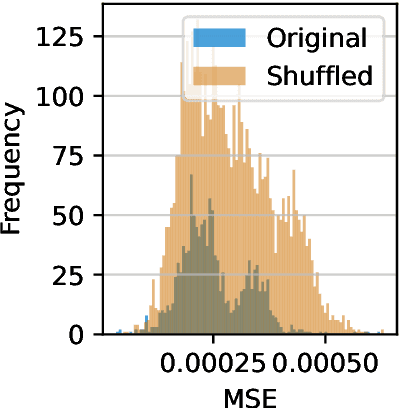
Abstract:Transformers have achieved state-of-the-art performance in language modeling tasks. However, the reasons behind their tremendous success are still unclear. In this paper, towards a better understanding, we train a Transformer model on a simple next token prediction task, where sequences are generated as a first-order autoregressive process $s_{t+1} = W s_t$. We show how a trained Transformer predicts the next token by first learning $W$ in-context, then applying a prediction mapping. We call the resulting procedure in-context autoregressive learning. More precisely, focusing on commuting orthogonal matrices $W$, we first show that a trained one-layer linear Transformer implements one step of gradient descent for the minimization of an inner objective function, when considering augmented tokens. When the tokens are not augmented, we characterize the global minima of a one-layer diagonal linear multi-head Transformer. Importantly, we exhibit orthogonality between heads and show that positional encoding captures trigonometric relations in the data. On the experimental side, we consider the general case of non-commuting orthogonal matrices and generalize our theoretical findings.
Implicit regularization of deep residual networks towards neural ODEs
Sep 03, 2023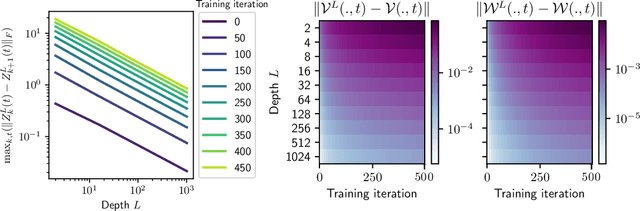
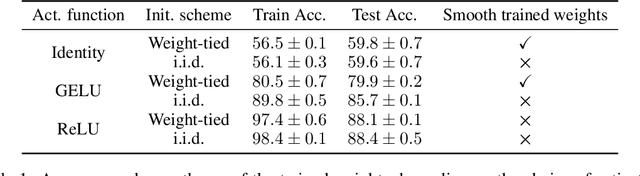
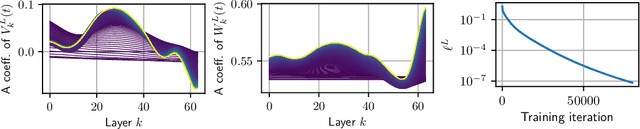
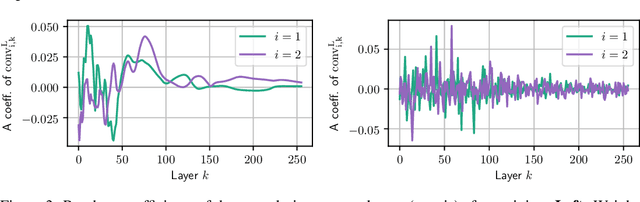
Abstract:Residual neural networks are state-of-the-art deep learning models. Their continuous-depth analog, neural ordinary differential equations (ODEs), are also widely used. Despite their success, the link between the discrete and continuous models still lacks a solid mathematical foundation. In this article, we take a step in this direction by establishing an implicit regularization of deep residual networks towards neural ODEs, for nonlinear networks trained with gradient flow. We prove that if the network is initialized as a discretization of a neural ODE, then such a discretization holds throughout training. Our results are valid for a finite training time, and also as the training time tends to infinity provided that the network satisfies a Polyak-Lojasiewicz condition. Importantly, this condition holds for a family of residual networks where the residuals are two-layer perceptrons with an overparameterization in width that is only linear, and implies the convergence of gradient flow to a global minimum. Numerical experiments illustrate our results.
Fast, Differentiable and Sparse Top-k: a Convex Analysis Perspective
Feb 06, 2023



Abstract:The top-k operator returns a k-sparse vector, where the non-zero values correspond to the k largest values of the input. Unfortunately, because it is a discontinuous function, it is difficult to incorporate in neural networks trained end-to-end with backpropagation. Recent works have considered differentiable relaxations, based either on regularization or perturbation techniques. However, to date, no approach is fully differentiable and sparse. In this paper, we propose new differentiable and sparse top-k operators. We view the top-k operator as a linear program over the permutahedron, the convex hull of permutations. We then introduce a p-norm regularization term to smooth out the operator, and show that its computation can be reduced to isotonic optimization. Our framework is significantly more general than the existing one and allows for example to express top-k operators that select values in magnitude. On the algorithmic side, in addition to pool adjacent violator (PAV) algorithms, we propose a new GPU/TPU-friendly Dykstra algorithm to solve isotonic optimization problems. We successfully use our operators to prune weights in neural networks, to fine-tune vision transformers, and as a router in sparse mixture of experts.
Vision Transformers provably learn spatial structure
Oct 13, 2022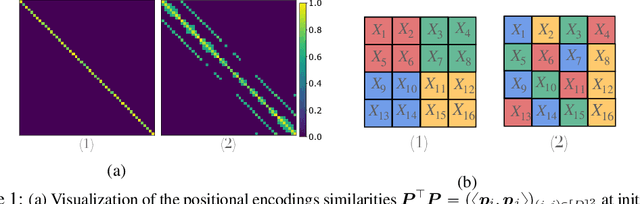
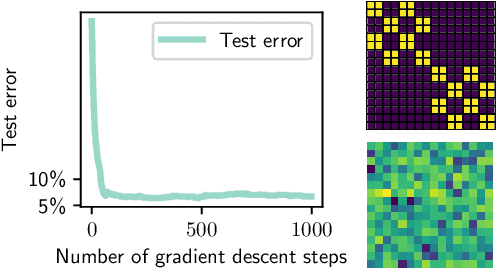
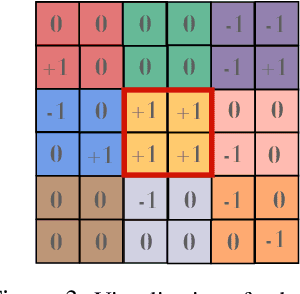
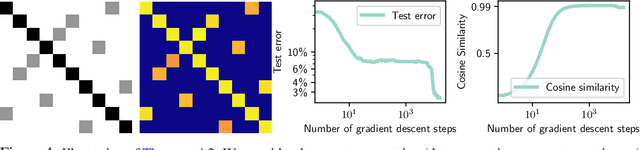
Abstract:Vision Transformers (ViTs) have achieved comparable or superior performance than Convolutional Neural Networks (CNNs) in computer vision. This empirical breakthrough is even more remarkable since, in contrast to CNNs, ViTs do not embed any visual inductive bias of spatial locality. Yet, recent works have shown that while minimizing their training loss, ViTs specifically learn spatially localized patterns. This raises a central question: how do ViTs learn these patterns by solely minimizing their training loss using gradient-based methods from random initialization? In this paper, we provide some theoretical justification of this phenomenon. We propose a spatially structured dataset and a simplified ViT model. In this model, the attention matrix solely depends on the positional encodings. We call this mechanism the positional attention mechanism. On the theoretical side, we consider a binary classification task and show that while the learning problem admits multiple solutions that generalize, our model implicitly learns the spatial structure of the dataset while generalizing: we call this phenomenon patch association. We prove that patch association helps to sample-efficiently transfer to downstream datasets that share the same structure as the pre-training one but differ in the features. Lastly, we empirically verify that a ViT with positional attention performs similarly to the original one on CIFAR-10/100, SVHN and ImageNet.
Do Residual Neural Networks discretize Neural Ordinary Differential Equations?
May 29, 2022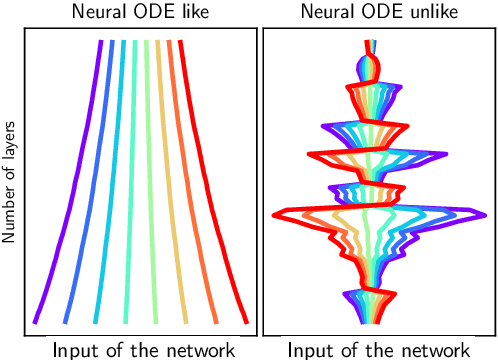
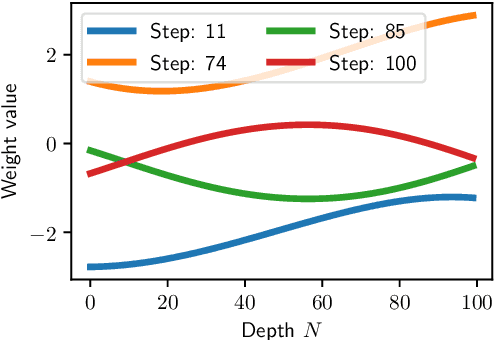
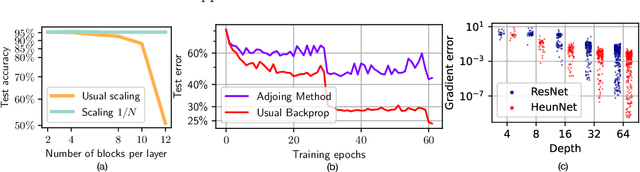
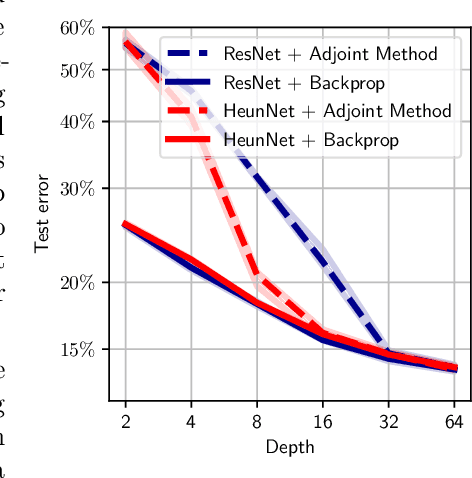
Abstract:Neural Ordinary Differential Equations (Neural ODEs) are the continuous analog of Residual Neural Networks (ResNets). We investigate whether the discrete dynamics defined by a ResNet are close to the continuous one of a Neural ODE. We first quantify the distance between the ResNet's hidden state trajectory and the solution of its corresponding Neural ODE. Our bound is tight and, on the negative side, does not go to 0 with depth N if the residual functions are not smooth with depth. On the positive side, we show that this smoothness is preserved by gradient descent for a ResNet with linear residual functions and small enough initial loss. It ensures an implicit regularization towards a limit Neural ODE at rate 1 over N, uniformly with depth and optimization time. As a byproduct of our analysis, we consider the use of a memory-free discrete adjoint method to train a ResNet by recovering the activations on the fly through a backward pass of the network, and show that this method theoretically succeeds at large depth if the residual functions are Lipschitz with the input. We then show that Heun's method, a second order ODE integration scheme, allows for better gradient estimation with the adjoint method when the residual functions are smooth with depth. We experimentally validate that our adjoint method succeeds at large depth, and that Heun method needs fewer layers to succeed. We finally use the adjoint method successfully for fine-tuning very deep ResNets without memory consumption in the residual layers.
Sinkformers: Transformers with Doubly Stochastic Attention
Oct 22, 2021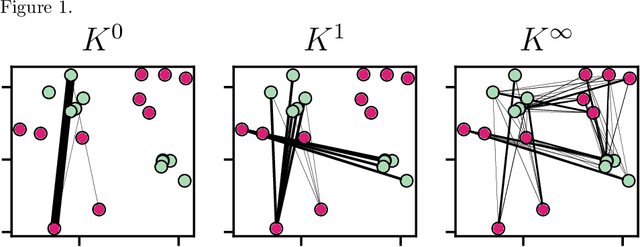
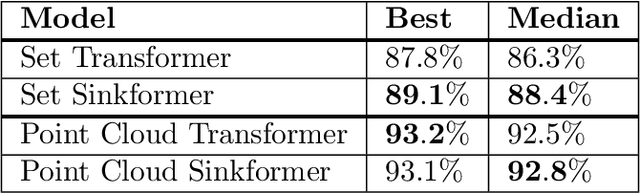
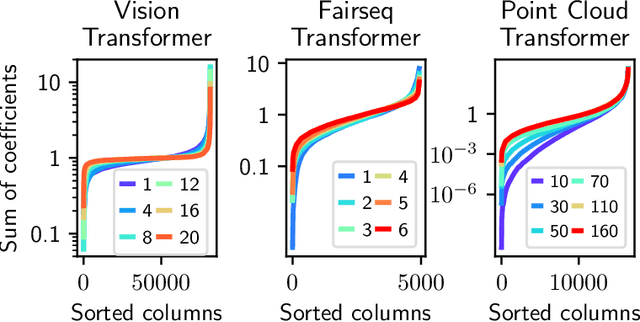

Abstract:Attention based models such as Transformers involve pairwise interactions between data points, modeled with a learnable attention matrix. Importantly, this attention matrix is normalized with the SoftMax operator, which makes it row-wise stochastic. In this paper, we propose instead to use Sinkhorn's algorithm to make attention matrices doubly stochastic. We call the resulting model a Sinkformer. We show that the row-wise stochastic attention matrices in classical Transformers get close to doubly stochastic matrices as the number of epochs increases, justifying the use of Sinkhorn normalization as an informative prior. On the theoretical side, we show that, unlike the SoftMax operation, this normalization makes it possible to understand the iterations of self-attention modules as a discretized gradient-flow for the Wasserstein metric. We also show in the infinite number of samples limit that, when rescaling both attention matrices and depth, Sinkformers operate a heat diffusion. On the experimental side, we show that Sinkformers enhance model accuracy in vision and natural language processing tasks. In particular, on 3D shapes classification, Sinkformers lead to a significant improvement.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge