Taking a Big Step: Large Learning Rates in Denoising Score Matching Prevent Memorization

Denoising score matching plays a pivotal role in the performance of diffusion-based generative models. However, the empirical optimal score--the exact solution to the denoising score matching--leads to memorization, where generated samples replicate the training data. Yet, in practice, only a moderate degree of memorization is observed, even without explicit regularization. In this paper, we investigate this phenomenon by uncovering an implicit regularization mechanism driven by large learning rates. Specifically, we show that in the small-noise regime, the empirical optimal score exhibits high irregularity. We then prove that, when trained by stochastic gradient descent with a large enough learning rate, neural networks cannot stably converge to a local minimum with arbitrarily small excess risk. Consequently, the learned score cannot be arbitrarily close to the empirical optimal score, thereby mitigating memorization. To make the analysis tractable, we consider one-dimensional data and two-layer neural networks. Experiments validate the crucial role of the learning rate in preventing memorization, even beyond the one-dimensional setting.

Implicit regularization of deep residual networks towards neural ODEs

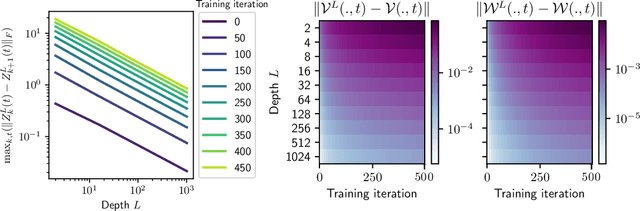
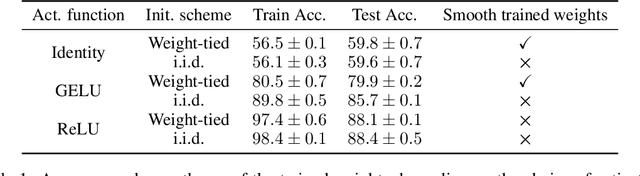
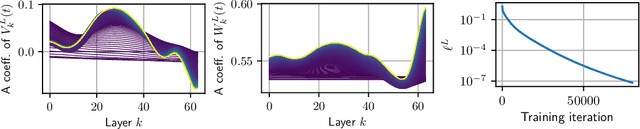
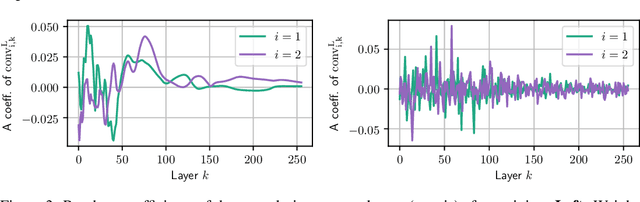
Residual neural networks are state-of-the-art deep learning models. Their continuous-depth analog, neural ordinary differential equations (ODEs), are also widely used. Despite their success, the link between the discrete and continuous models still lacks a solid mathematical foundation. In this article, we take a step in this direction by establishing an implicit regularization of deep residual networks towards neural ODEs, for nonlinear networks trained with gradient flow. We prove that if the network is initialized as a discretization of a neural ODE, then such a discretization holds throughout training. Our results are valid for a finite training time, and also as the training time tends to infinity provided that the network satisfies a Polyak-Lojasiewicz condition. Importantly, this condition holds for a family of residual networks where the residuals are two-layer perceptrons with an overparameterization in width that is only linear, and implies the convergence of gradient flow to a global minimum. Numerical experiments illustrate our results.