Do Residual Neural Networks discretize Neural Ordinary Differential Equations?
Paper and Code
May 29, 2022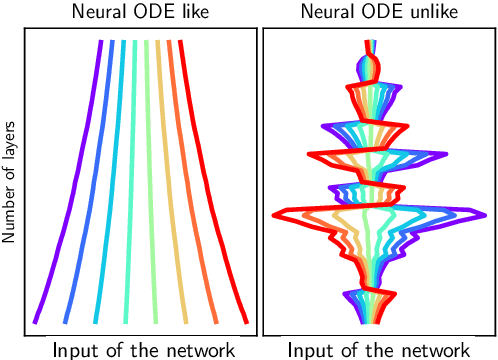
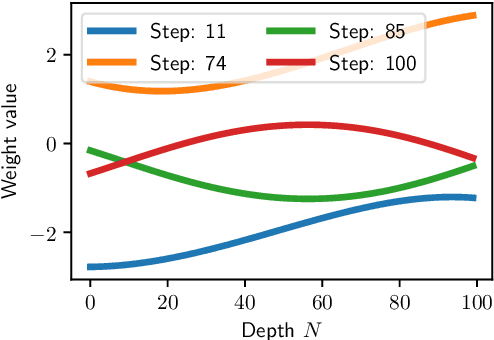
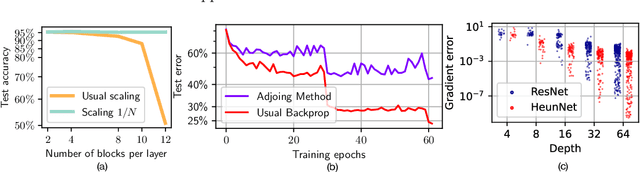
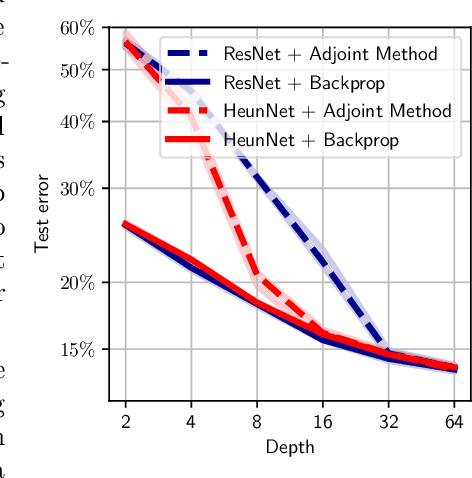
Neural Ordinary Differential Equations (Neural ODEs) are the continuous analog of Residual Neural Networks (ResNets). We investigate whether the discrete dynamics defined by a ResNet are close to the continuous one of a Neural ODE. We first quantify the distance between the ResNet's hidden state trajectory and the solution of its corresponding Neural ODE. Our bound is tight and, on the negative side, does not go to 0 with depth N if the residual functions are not smooth with depth. On the positive side, we show that this smoothness is preserved by gradient descent for a ResNet with linear residual functions and small enough initial loss. It ensures an implicit regularization towards a limit Neural ODE at rate 1 over N, uniformly with depth and optimization time. As a byproduct of our analysis, we consider the use of a memory-free discrete adjoint method to train a ResNet by recovering the activations on the fly through a backward pass of the network, and show that this method theoretically succeeds at large depth if the residual functions are Lipschitz with the input. We then show that Heun's method, a second order ODE integration scheme, allows for better gradient estimation with the adjoint method when the residual functions are smooth with depth. We experimentally validate that our adjoint method succeeds at large depth, and that Heun method needs fewer layers to succeed. We finally use the adjoint method successfully for fine-tuning very deep ResNets without memory consumption in the residual layers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge