Robust Sublinear Convergence Rates for Iterative Bregman Projections

Entropic regularization provides a simple way to approximate linear programs whose constraints split into two (or more) tractable blocks. The resulting objectives are amenable to cyclic Kullback-Leibler (KL) Bregman projections, with the classical Sinkhorn algorithm for optimal transport (balanced, unbalanced, gradient flows, barycenters, \dots) as the canonical example. Assuming uniformly bounded primal mass and dual radius, we prove that the dual objective of these KL projections decreases at an $O(1/k)$ rate with a constant that scales only linearly in $1/γ$, where $γ$ is the entropic regularization parameter. This extends the guarantees known for entropic optimal transport to any such linearly constrained problem. Following the terminology introduced in [Chizat et al 2025], we call such rates "robust", because this mild dependence on $γ$ underpins favorable complexity bounds for approximating the unregularized problem via alternating KL projections. The crucial aspect of the analysis is that the dual radius should be measured according to a block-quotient dual seminorm, which depends on the structure of the split of the constraint into blocks. As an application, we derive the flow-Sinkhorn algorithm for the Wasserstein-1 distance on graphs. It achieves $ε$-additive accuracy on the transshipment cost in $O(p/ε^{4})$ arithmetic operations, where $p$ is the number of edges.

Token Sample Complexity of Attention

As context windows in large language models continue to expand, it is essential to characterize how attention behaves at extreme sequence lengths. We introduce token-sample complexity: the rate at which attention computed on $n$ tokens converges to its infinite-token limit. We estimate finite-$n$ convergence bounds at two levels: pointwise uniform convergence of the attention map, and convergence of moments for the transformed token distribution. For compactly supported (and more generally sub-Gaussian) distributions, our first result shows that the attention map converges uniformly on a ball of radius $R$ at rate $C(R)/\sqrt{n}$, where $C(R)$ grows exponentially with $R$. For large $R$, this estimate loses practical value, and our second result addresses this issue by establishing convergence rates for the moments of the transformed distribution (the token output of the attention layer). In this case, the rate is $C'(R)/n^β$ with $β<\tfrac{1}{2}$, and $C'(R)$ depends polynomially on the size of the support of the distribution. The exponent $β$ depends on the attention geometry and the spectral properties of the tokens distribution. We also examine the regime in which the attention parameter tends to infinity and the softmax approaches a hardmax, and in this setting, we establish a logarithmic rate of convergence. Experiments on synthetic Gaussian data and real BERT models on Wikipedia text confirm our predictions.

Intrinsic training dynamics of deep neural networks

A fundamental challenge in the theory of deep learning is to understand whether gradient-based training in high-dimensional parameter spaces can be captured by simpler, lower-dimensional structures, leading to so-called implicit bias. As a stepping stone, we study when a gradient flow on a high-dimensional variable $\theta$ implies an intrinsic gradient flow on a lower-dimensional variable $z = \phi(\theta)$, for an architecture-related function $\phi$. We express a so-called intrinsic dynamic property and show how it is related to the study of conservation laws associated with the factorization $\phi$. This leads to a simple criterion based on the inclusion of kernels of linear maps which yields a necessary condition for this property to hold. We then apply our theory to general ReLU networks of arbitrary depth and show that, for any initialization, it is possible to rewrite the flow as an intrinsic dynamic in a lower dimension that depends only on $z$ and the initialization, when $\phi$ is the so-called path-lifting. In the case of linear networks with $\phi$ the product of weight matrices, so-called balanced initializations are also known to enable such a dimensionality reduction; we generalize this result to a broader class of {\em relaxed balanced} initializations, showing that, in certain configurations, these are the \emph{only} initializations that ensure the intrinsic dynamic property. Finally, for the linear neural ODE associated with the limit of infinitely deep linear networks, with relaxed balanced initialization, we explicitly express the corresponding intrinsic dynamics.

Transformative or Conservative? Conservation laws for ResNets and Transformers

While conservation laws in gradient flow training dynamics are well understood for (mostly shallow) ReLU and linear networks, their study remains largely unexplored for more practical architectures. This paper bridges this gap by deriving and analyzing conservation laws for modern architectures, with a focus on convolutional ResNets and Transformer networks. For this, we first show that basic building blocks such as ReLU (or linear) shallow networks, with or without convolution, have easily expressed conservation laws, and no more than the known ones. In the case of a single attention layer, we also completely describe all conservation laws, and we show that residual blocks have the same conservation laws as the same block without a skip connection. We then introduce the notion of conservation laws that depend only on a subset of parameters (corresponding e.g. to a pair of consecutive layers, to a residual block, or to an attention layer). We demonstrate that the characterization of such laws can be reduced to the analysis of the corresponding building block in isolation. Finally, we examine how these newly discovered conservation principles, initially established in the continuous gradient flow regime, persist under discrete optimization dynamics, particularly in the context of Stochastic Gradient Descent (SGD).

Learning from Samples: Inverse Problems over measures via Sharpened Fenchel-Young Losses

Estimating parameters from samples of an optimal probability distribution is essential in applications ranging from socio-economic modeling to biological system analysis. In these settings, the probability distribution arises as the solution to an optimization problem that captures either static interactions among agents or the dynamic evolution of a system over time. Our approach relies on minimizing a new class of loss functions, called sharpened Fenchel-Young losses, which measure the sub-optimality gap of the optimization problem over the space of measures. We study the stability of this estimation method when only a finite number of sample is available. The parameters to be estimated typically correspond to a cost function in static problems and to a potential function in dynamic problems. To analyze stability, we introduce a general methodology that leverages the strong convexity of the loss function together with the sample complexity of the forward optimization problem. Our analysis emphasizes two specific settings in the context of optimal transport, where our method provides explicit stability guarantees: The first is inverse unbalanced optimal transport (iUOT) with entropic regularization, where the parameters to estimate are cost functions that govern transport computations; this method has applications such as link prediction in machine learning. The second is inverse gradient flow (iJKO), where the objective is to recover a potential function that drives the evolution of a probability distribution via the Jordan-Kinderlehrer-Otto (JKO) time-discretization scheme; this is particularly relevant for understanding cell population dynamics in single-cell genomics. Finally, we validate our approach through numerical experiments on Gaussian distributions, where closed-form solutions are available, to demonstrate the practical performance of our methods

Optimal Transport for Machine Learners

Optimal Transport is a foundational mathematical theory that connects optimization, partial differential equations, and probability. It offers a powerful framework for comparing probability distributions and has recently become an important tool in machine learning, especially for designing and evaluating generative models. These course notes cover the fundamental mathematical aspects of OT, including the Monge and Kantorovich formulations, Brenier's theorem, the dual and dynamic formulations, the Bures metric on Gaussian distributions, and gradient flows. It also introduces numerical methods such as linear programming, semi-discrete solvers, and entropic regularization. Applications in machine learning include topics like training neural networks via gradient flows, token dynamics in transformers, and the structure of GANs and diffusion models. These notes focus primarily on mathematical content rather than deep learning techniques.

Ultra-fast feature learning for the training of two-layer neural networks in the two-timescale regime

We study the convergence of gradient methods for the training of mean-field single hidden layer neural networks with square loss. Observing this is a separable non-linear least-square problem which is linear w.r.t. the outer layer's weights, we consider a Variable Projection (VarPro) or two-timescale learning algorithm, thereby eliminating the linear variables and reducing the learning problem to the training of the feature distribution. Whereas most convergence rates or the training of neural networks rely on a neural tangent kernel analysis where features are fixed, we show such a strategy enables provable convergence rates for the sampling of a teacher feature distribution. Precisely, in the limit where the regularization strength vanishes, we show that the dynamic of the feature distribution corresponds to a weighted ultra-fast diffusion equation. Relying on recent results on the asymptotic behavior of such PDEs, we obtain guarantees for the convergence of the trained feature distribution towards the teacher feature distribution in a teacher-student setup.

From Denoising Score Matching to Langevin Sampling: A Fine-Grained Error Analysis in the Gaussian Setting

Sampling from an unknown distribution, accessible only through discrete samples, is a fundamental problem at the core of generative AI. The current state-of-the-art methods follow a two-step process: first estimating the score function (the gradient of a smoothed log-distribution) and then applying a gradient-based sampling algorithm. The resulting distribution's correctness can be impacted by several factors: the generalization error due to a finite number of initial samples, the error in score matching, and the diffusion error introduced by the sampling algorithm. In this paper, we analyze the sampling process in a simple yet representative setting-sampling from Gaussian distributions using a Langevin diffusion sampler. We provide a sharp analysis of the Wasserstein sampling error that arises from the multiple sources of error throughout the pipeline. This allows us to rigorously track how the anisotropy of the data distribution (encoded by its power spectrum) interacts with key parameters of the end-to-end sampling method, including the noise amplitude, the step sizes in both score matching and diffusion, and the number of initial samples. Notably, we show that the Wasserstein sampling error can be expressed as a kernel-type norm of the data power spectrum, where the specific kernel depends on the method parameters. This result provides a foundation for further analysis of the tradeoffs involved in optimizing sampling accuracy, such as adapting the noise amplitude to the choice of step sizes.

A Unified Perspective on the Dynamics of Deep Transformers

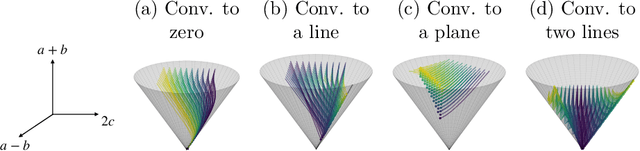
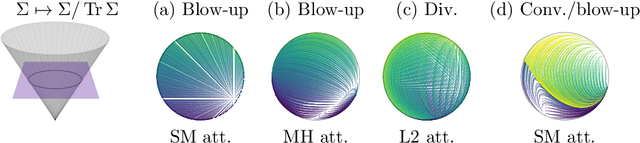
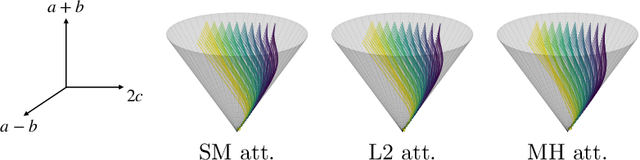
Transformers, which are state-of-the-art in most machine learning tasks, represent the data as sequences of vectors called tokens. This representation is then exploited by the attention function, which learns dependencies between tokens and is key to the success of Transformers. However, the iterative application of attention across layers induces complex dynamics that remain to be fully understood. To analyze these dynamics, we identify each input sequence with a probability measure and model its evolution as a Vlasov equation called Transformer PDE, whose velocity field is non-linear in the probability measure. Our first set of contributions focuses on compactly supported initial data. We show the Transformer PDE is well-posed and is the mean-field limit of an interacting particle system, thus generalizing and extending previous analysis to several variants of self-attention: multi-head attention, L2 attention, Sinkhorn attention, Sigmoid attention, and masked attention--leveraging a conditional Wasserstein framework. In a second set of contributions, we are the first to study non-compactly supported initial conditions, by focusing on Gaussian initial data. Again for different types of attention, we show that the Transformer PDE preserves the space of Gaussian measures, which allows us to analyze the Gaussian case theoretically and numerically to identify typical behaviors. This Gaussian analysis captures the evolution of data anisotropy through a deep Transformer. In particular, we highlight a clustering phenomenon that parallels previous results in the non-normalized discrete case.

Towards Understanding the Universality of Transformers for Next-Token Prediction

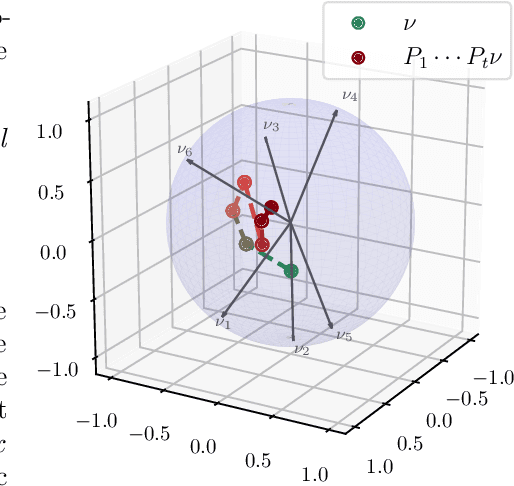
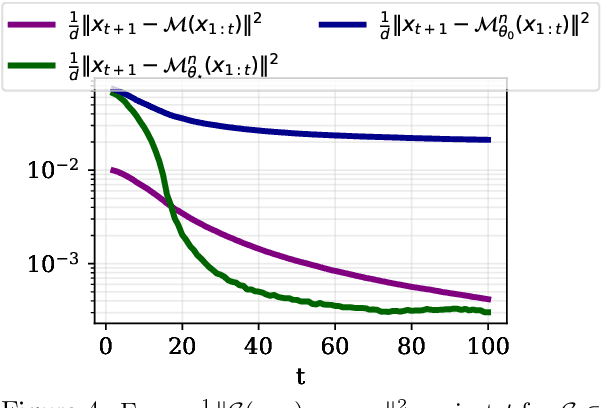
Causal Transformers are trained to predict the next token for a given context. While it is widely accepted that self-attention is crucial for encoding the causal structure of sequences, the precise underlying mechanism behind this in-context autoregressive learning ability remains unclear. In this paper, we take a step towards understanding this phenomenon by studying the approximation ability of Transformers for next-token prediction. Specifically, we explore the capacity of causal Transformers to predict the next token $x_{t+1}$ given an autoregressive sequence $(x_1, \dots, x_t)$ as a prompt, where $ x_{t+1} = f(x_t) $, and $ f $ is a context-dependent function that varies with each sequence. On the theoretical side, we focus on specific instances, namely when $ f $ is linear or when $ (x_t)_{t \geq 1} $ is periodic. We explicitly construct a Transformer (with linear, exponential, or softmax attention) that learns the mapping $f$ in-context through a causal kernel descent method. The causal kernel descent method we propose provably estimates $x_{t+1} $ based solely on past and current observations $ (x_1, \dots, x_t) $, with connections to the Kaczmarz algorithm in Hilbert spaces. We present experimental results that validate our theoretical findings and suggest their applicability to more general mappings $f$.