Samuel Hurault
DeepInverse: A Python package for solving imaging inverse problems with deep learning
May 26, 2025Abstract:DeepInverse is an open-source PyTorch-based library for solving imaging inverse problems. The library covers all crucial steps in image reconstruction from the efficient implementation of forward operators (e.g., optics, MRI, tomography), to the definition and resolution of variational problems and the design and training of advanced neural network architectures. In this paper, we describe the main functionality of the library and discuss the main design choices.
From Denoising Score Matching to Langevin Sampling: A Fine-Grained Error Analysis in the Gaussian Setting
Mar 14, 2025Abstract:Sampling from an unknown distribution, accessible only through discrete samples, is a fundamental problem at the core of generative AI. The current state-of-the-art methods follow a two-step process: first estimating the score function (the gradient of a smoothed log-distribution) and then applying a gradient-based sampling algorithm. The resulting distribution's correctness can be impacted by several factors: the generalization error due to a finite number of initial samples, the error in score matching, and the diffusion error introduced by the sampling algorithm. In this paper, we analyze the sampling process in a simple yet representative setting-sampling from Gaussian distributions using a Langevin diffusion sampler. We provide a sharp analysis of the Wasserstein sampling error that arises from the multiple sources of error throughout the pipeline. This allows us to rigorously track how the anisotropy of the data distribution (encoded by its power spectrum) interacts with key parameters of the end-to-end sampling method, including the noise amplitude, the step sizes in both score matching and diffusion, and the number of initial samples. Notably, we show that the Wasserstein sampling error can be expressed as a kernel-type norm of the data power spectrum, where the specific kernel depends on the method parameters. This result provides a foundation for further analysis of the tradeoffs involved in optimizing sampling accuracy, such as adapting the noise amplitude to the choice of step sizes.
Reconstruct Anything Model: a lightweight foundation model for computational imaging
Mar 11, 2025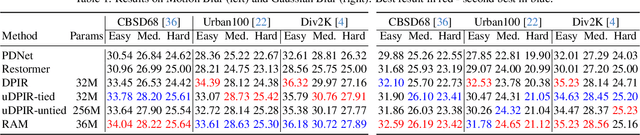
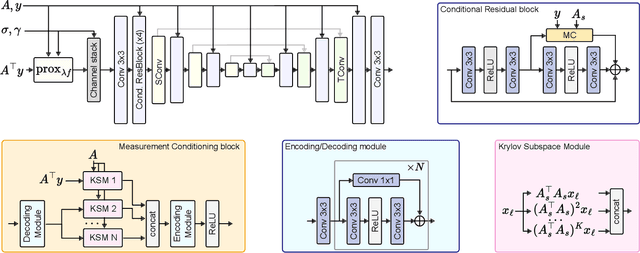
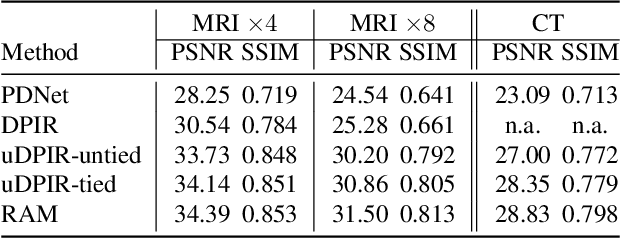
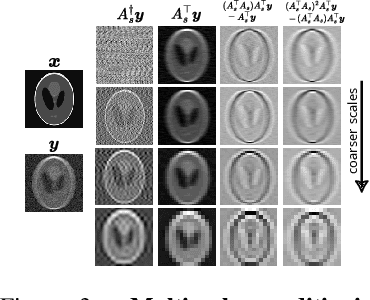
Abstract:Most existing learning-based methods for solving imaging inverse problems can be roughly divided into two classes: iterative algorithms, such as plug-and-play and diffusion methods, that leverage pretrained denoisers, and unrolled architectures that are trained end-to-end for specific imaging problems. Iterative methods in the first class are computationally costly and often provide suboptimal reconstruction performance, whereas unrolled architectures are generally specific to a single inverse problem and require expensive training. In this work, we propose a novel non-iterative, lightweight architecture that incorporates knowledge about the forward operator (acquisition physics and noise parameters) without relying on unrolling. Our model is trained to solve a wide range of inverse problems beyond denoising, including deblurring, magnetic resonance imaging, computed tomography, inpainting, and super-resolution. The proposed model can be easily adapted to unseen inverse problems or datasets with a few fine-tuning steps (up to a few images) in a self-supervised way, without ground-truth references. Throughout a series of experiments, we demonstrate state-of-the-art performance from medical imaging to low-photon imaging and microscopy.
Convergent plug-and-play with proximal denoiser and unconstrained regularization parameter
Nov 02, 2023Abstract:In this work, we present new proofs of convergence for Plug-and-Play (PnP) algorithms. PnP methods are efficient iterative algorithms for solving image inverse problems where regularization is performed by plugging a pre-trained denoiser in a proximal algorithm, such as Proximal Gradient Descent (PGD) or Douglas-Rachford Splitting (DRS). Recent research has explored convergence by incorporating a denoiser that writes exactly as a proximal operator. However, the corresponding PnP algorithm has then to be run with stepsize equal to $1$. The stepsize condition for nonconvex convergence of the proximal algorithm in use then translates to restrictive conditions on the regularization parameter of the inverse problem. This can severely degrade the restoration capacity of the algorithm. In this paper, we present two remedies for this limitation. First, we provide a novel convergence proof for PnP-DRS that does not impose any restrictions on the regularization parameter. Second, we examine a relaxed version of the PGD algorithm that converges across a broader range of regularization parameters. Our experimental study, conducted on deblurring and super-resolution experiments, demonstrate that both of these solutions enhance the accuracy of image restoration.
Convergent Bregman Plug-and-Play Image Restoration for Poisson Inverse Problems
Jun 06, 2023



Abstract:Plug-and-Play (PnP) methods are efficient iterative algorithms for solving ill-posed image inverse problems. PnP methods are obtained by using deep Gaussian denoisers instead of the proximal operator or the gradient-descent step within proximal algorithms. Current PnP schemes rely on data-fidelity terms that have either Lipschitz gradients or closed-form proximal operators, which is not applicable to Poisson inverse problems. Based on the observation that the Gaussian noise is not the adequate noise model in this setting, we propose to generalize PnP using theBregman Proximal Gradient (BPG) method. BPG replaces the Euclidean distance with a Bregman divergence that can better capture the smoothness properties of the problem. We introduce the Bregman Score Denoiser specifically parametrized and trained for the new Bregman geometry and prove that it corresponds to the proximal operator of a nonconvex potential. We propose two PnP algorithms based on the Bregman Score Denoiser for solving Poisson inverse problems. Extending the convergence results of BPG in the nonconvex settings, we show that the proposed methods converge, targeting stationary points of an explicit global functional. Experimental evaluations conducted on various Poisson inverse problems validate the convergence results and showcase effective restoration performance.
A relaxed proximal gradient descent algorithm for convergent plug-and-play with proximal denoiser
Jan 31, 2023


Abstract:This paper presents a new convergent Plug-and-Play (PnP) algorithm. PnP methods are efficient iterative algorithms for solving image inverse problems formulated as the minimization of the sum of a data-fidelity term and a regularization term. PnP methods perform regularization by plugging a pre-trained denoiser in a proximal algorithm, such as Proximal Gradient Descent (PGD). To ensure convergence of PnP schemes, many works study specific parametrizations of deep denoisers. However, existing results require either unverifiable or suboptimal hypotheses on the denoiser, or assume restrictive conditions on the parameters of the inverse problem. Observing that these limitations can be due to the proximal algorithm in use, we study a relaxed version of the PGD algorithm for minimizing the sum of a convex function and a weakly convex one. When plugged with a relaxed proximal denoiser, we show that the proposed PnP-$\alpha$PGD algorithm converges for a wider range of regularization parameters, thus allowing more accurate image restoration.
Self-Consistent Velocity Matching of Probability Flows
Jan 31, 2023Abstract:We present a discretization-free scalable framework for solving a large class of mass-conserving partial differential equations (PDEs), including the time-dependent Fokker-Planck equation and the Wasserstein gradient flow. The main observation is that the time-varying velocity field of the PDE solution needs to be self-consistent: it must satisfy a fixed-point equation involving the flow characterized by the same velocity field. By parameterizing the flow as a time-dependent neural network, we propose an end-to-end iterative optimization framework called self-consistent velocity matching to solve this class of PDEs. Compared to existing approaches, our method does not suffer from temporal or spatial discretization, covers a wide range of PDEs, and scales to high dimensions. Experimentally, our method recovers analytical solutions accurately when they are available and achieves comparable or better performance in high dimensions with less training time compared to recent large-scale JKO-based methods that are designed for solving a more restrictive family of PDEs.
An Analysis of Generative Methods for Multiple Image Inpainting
May 04, 2022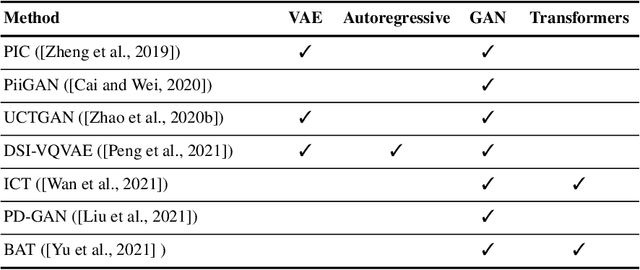
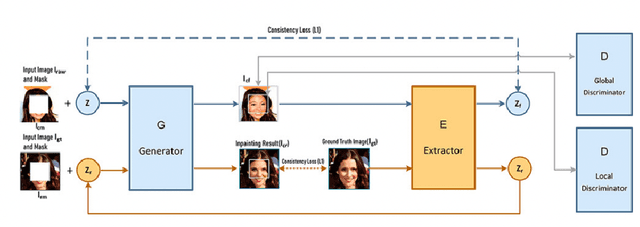
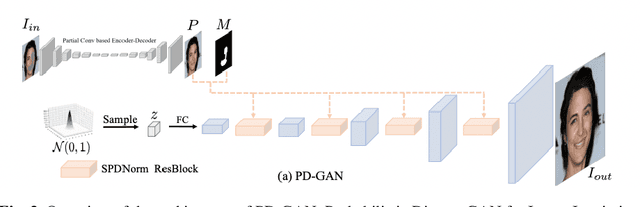
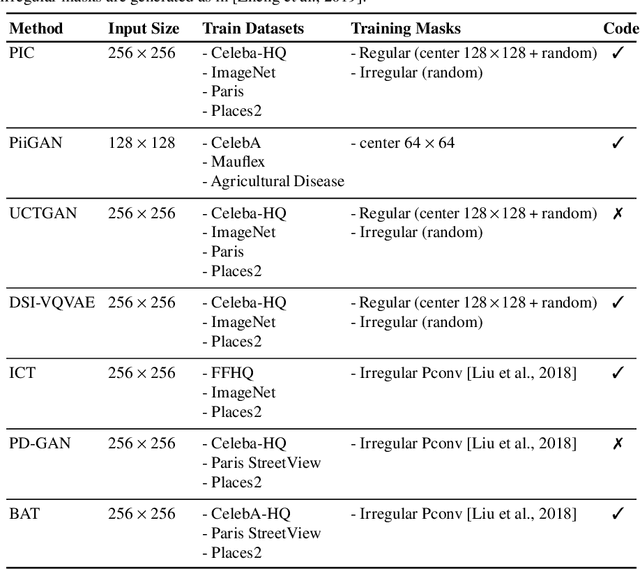
Abstract:Image inpainting refers to the restoration of an image with missing regions in a way that is not detectable by the observer. The inpainting regions can be of any size and shape. This is an ill-posed inverse problem that does not have a unique solution. In this work, we focus on learning-based image completion methods for multiple and diverse inpainting which goal is to provide a set of distinct solutions for a given damaged image. These methods capitalize on the probabilistic nature of certain generative models to sample various solutions that coherently restore the missing content. Along the chapter, we will analyze the underlying theory and analyze the recent proposals for multiple inpainting. To investigate the pros and cons of each method, we present quantitative and qualitative comparisons, on common datasets, regarding both the quality and the diversity of the set of inpainted solutions. Our analysis allows us to identify the most successful generative strategies in both inpainting quality and inpainting diversity. This task is closely related to the learning of an accurate probability distribution of images. Depending on the dataset in use, the challenges that entail the training of such a model will be discussed through the analysis.
Proximal denoiser for convergent plug-and-play optimization with nonconvex regularization
Jan 31, 2022

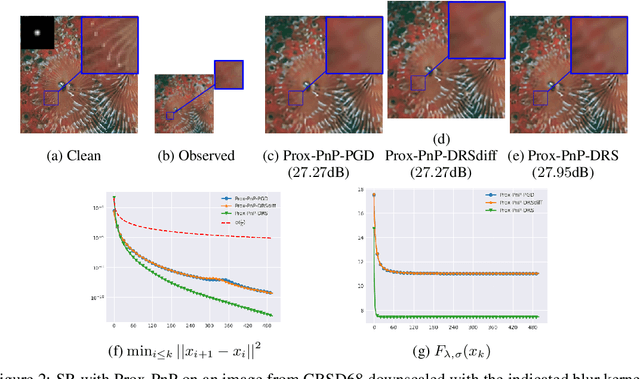
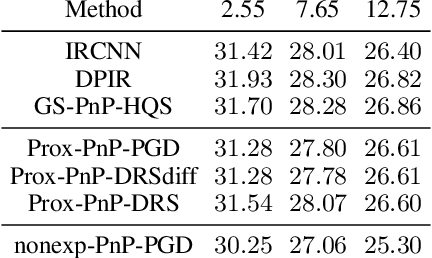
Abstract:Plug-and-Play (PnP) methods solve ill-posed inverse problems through iterative proximal algorithms by replacing a proximal operator by a denoising operation. When applied with deep neural network denoisers, these methods have shown state-of-the-art visual performance for image restoration problems. However, their theoretical convergence analysis is still incomplete. Most of the existing convergence results consider nonexpansive denoisers, which is non-realistic, or limit their analysis to strongly convex data-fidelity terms in the inverse problem to solve. Recently, it was proposed to train the denoiser as a gradient descent step on a functional parameterized by a deep neural network. Using such a denoiser guarantees the convergence of the PnP version of the Half-Quadratic-Splitting (PnP-HQS) iterative algorithm. In this paper, we show that this gradient denoiser can actually correspond to the proximal operator of another scalar function. Given this new result, we exploit the convergence theory of proximal algorithms in the nonconvex setting to obtain convergence results for PnP-PGD (Proximal Gradient Descent) and PnP-ADMM (Alternating Direction Method of Multipliers). When built on top of a smooth gradient denoiser, we show that PnP-PGD and PnP-ADMM are convergent and target stationary points of an explicit functional. These convergence results are confirmed with numerical experiments on deblurring, super-resolution and inpainting.
Gradient Step Denoiser for convergent Plug-and-Play
Oct 07, 2021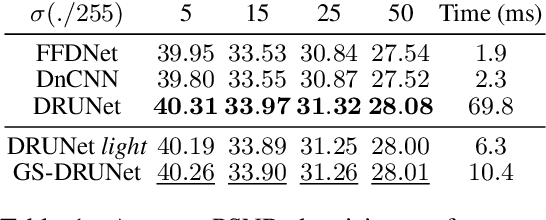
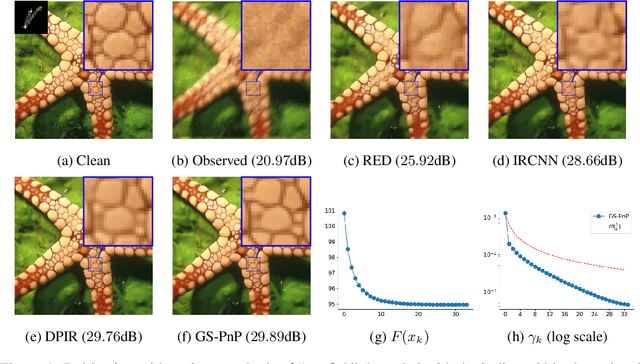
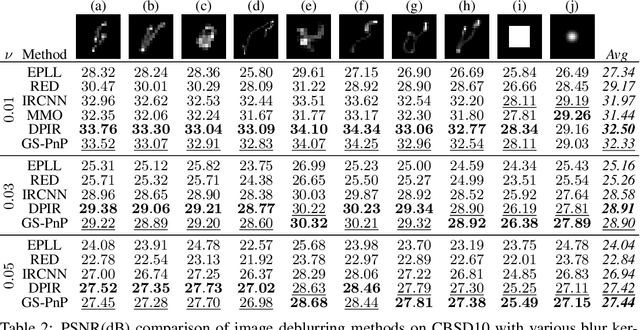
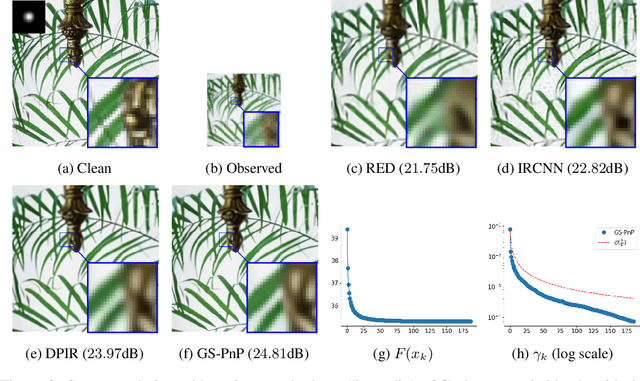
Abstract:Plug-and-Play methods constitute a class of iterative algorithms for imaging problems where regularization is performed by an off-the-shelf denoiser. Although Plug-and-Play methods can lead to tremendous visual performance for various image problems, the few existing convergence guarantees are based on unrealistic (or suboptimal) hypotheses on the denoiser, or limited to strongly convex data terms. In this work, we propose a new type of Plug-and-Play methods, based on half-quadratic splitting, for which the denoiser is realized as a gradient descent step on a functional parameterized by a deep neural network. Exploiting convergence results for proximal gradient descent algorithms in the non-convex setting, we show that the proposed Plug-and-Play algorithm is a convergent iterative scheme that targets stationary points of an explicit global functional. Besides, experiments show that it is possible to learn such a deep denoiser while not compromising the performance in comparison to other state-of-the-art deep denoisers used in Plug-and-Play schemes. We apply our proximal gradient algorithm to various ill-posed inverse problems, e.g. deblurring, super-resolution and inpainting. For all these applications, numerical results empirically confirm the convergence results. Experiments also show that this new algorithm reaches state-of-the-art performance, both quantitatively and qualitatively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge