Detection and Positive Reconstruction of Cognitive Distortion sentences: Mandarin Dataset and Evaluation

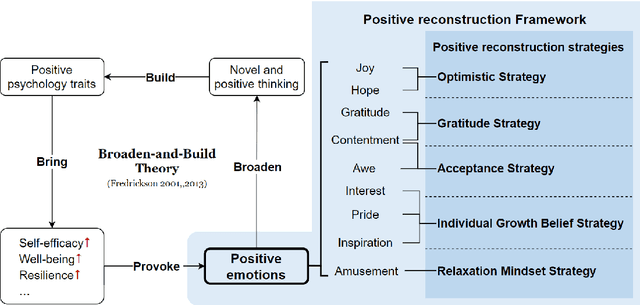
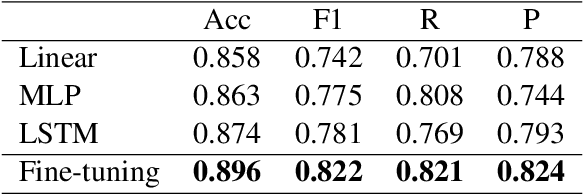
This research introduces a Positive Reconstruction Framework based on positive psychology theory. Overcoming negative thoughts can be challenging, our objective is to address and reframe them through a positive reinterpretation. To tackle this challenge, a two-fold approach is necessary: identifying cognitive distortions and suggesting a positively reframed alternative while preserving the original thought's meaning. Recent studies have investigated the application of Natural Language Processing (NLP) models in English for each stage of this process. In this study, we emphasize the theoretical foundation for the Positive Reconstruction Framework, grounded in broaden-and-build theory. We provide a shared corpus containing 4001 instances for detecting cognitive distortions and 1900 instances for positive reconstruction in Mandarin. Leveraging recent NLP techniques, including transfer learning, fine-tuning pretrained networks, and prompt engineering, we demonstrate the effectiveness of automated tools for both tasks. In summary, our study contributes to multilingual positive reconstruction, highlighting the effectiveness of NLP in cognitive distortion detection and positive reconstruction.

Extension of Recurrent Kernels to different Reservoir Computing topologies

Reservoir Computing (RC) has become popular in recent years due to its fast and efficient computational capabilities. Standard RC has been shown to be equivalent in the asymptotic limit to Recurrent Kernels, which helps in analyzing its expressive power. However, many well-established RC paradigms, such as Leaky RC, Sparse RC, and Deep RC, are yet to be analyzed in such a way. This study aims to fill this gap by providing an empirical analysis of the equivalence of specific RC architectures with their corresponding Recurrent Kernel formulation. We conduct a convergence study by varying the activation function implemented in each architecture. Our study also sheds light on the role of sparse connections in RC architectures and propose an optimal sparsity level that depends on the reservoir size. Furthermore, our systematic analysis shows that in Deep RC models, convergence is better achieved with successive reservoirs of decreasing sizes.

Asymptotic Stability in Reservoir Computing

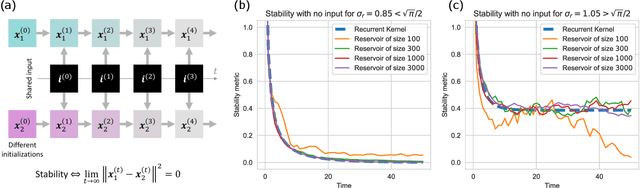
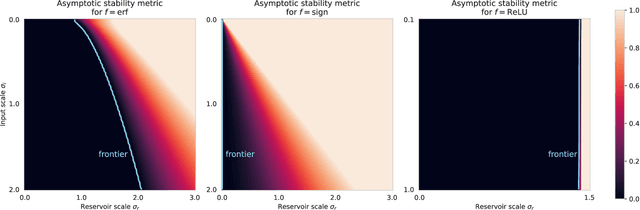
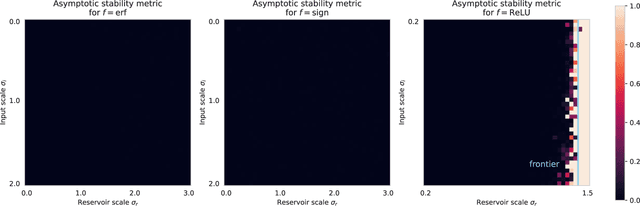
Reservoir Computing is a class of Recurrent Neural Networks with internal weights fixed at random. Stability relates to the sensitivity of the network state to perturbations. It is an important property in Reservoir Computing as it directly impacts performance. In practice, it is desirable to stay in a stable regime, where the effect of perturbations does not explode exponentially, but also close to the chaotic frontier where reservoir dynamics are rich. Open questions remain today regarding input regularization and discontinuous activation functions. In this work, we use the recurrent kernel limit to draw new insights on stability in reservoir computing. This limit corresponds to large reservoir sizes, and it already becomes relevant for reservoirs with a few hundred neurons. We obtain a quantitative characterization of the frontier between stability and chaos, which can greatly benefit hyperparameter tuning. In a broader sense, our results contribute to understanding the complex dynamics of Recurrent Neural Networks.

Physics-based neural network for non-invasive control of coherent light in scattering media

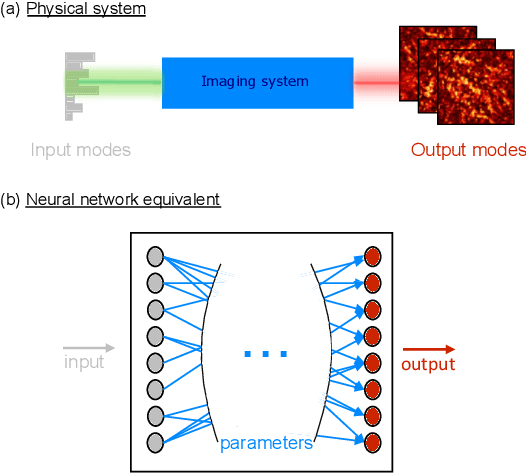
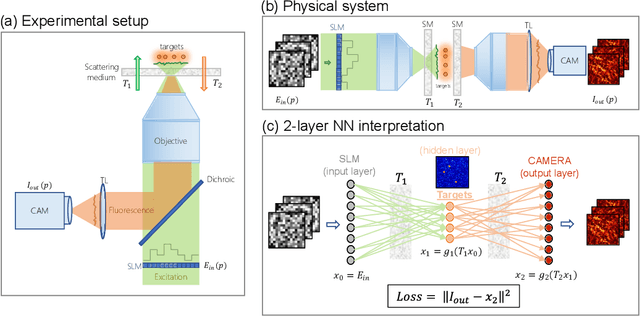
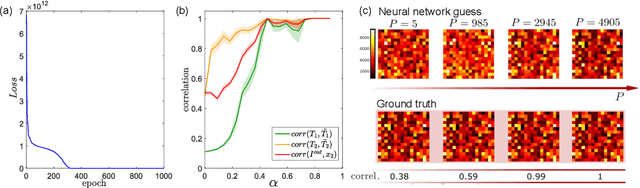
Optical imaging through complex media, such as biological tissues or fog, is challenging due to light scattering. In the multiple scattering regime, wavefront shaping provides an effective method to retrieve information; it relies on measuring how the propagation of different optical wavefronts are impacted by scattering. Based on this principle, several wavefront shaping techniques were successfully developed, but most of them are highly invasive and limited to proof-of-principle experiments. Here, we propose to use a neural network approach to non-invasively characterize and control light scattering inside the medium and also to retrieve information of hidden objects buried within it. Unlike most of the recently-proposed approaches, the architecture of our neural network with its layers, connected nodes and activation functions has a true physical meaning as it mimics the propagation of light in our optical system. It is trained with an experimentally-measured input/output dataset built from a series of incident light patterns and corresponding camera snapshots. We apply our physics-based neural network to a fluorescence microscope in epi-configuration and demonstrate its performance through numerical simulations and experiments. This flexible method can include physical priors and we show that it can be applied to other systems as, for example, non-linear or coherent contrast mechanisms.

Bayesian Inversion for Nonlinear Imaging Models using Deep Generative Priors

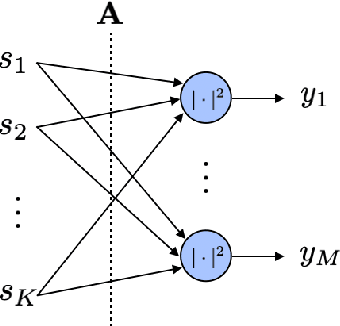
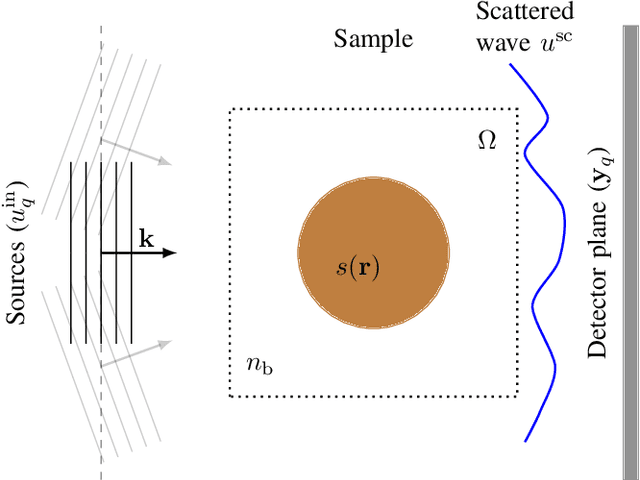
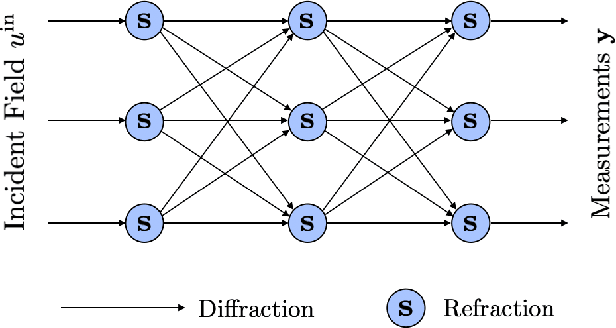
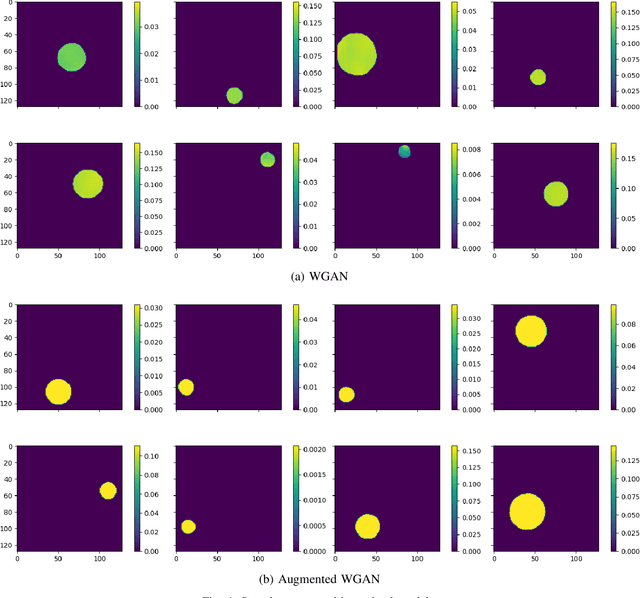
Most modern imaging systems involve a computational reconstruction pipeline to infer the image of interest from acquired measurements. The Bayesian reconstruction framework relies on the characterization of the posterior distribution, which depends on a model of the imaging system and prior knowledge on the image, for solving such inverse problems. Here, the choice of the prior distribution is critical for obtaining high-quality estimates. In this work, we use deep generative models to represent the prior distribution. We develop a posterior sampling scheme for the class of nonlinear inverse problems where the forward model has a neural-network-like structure. This class includes most existing imaging modalities. We introduce the notion of augmented generative models in order to suitably handle quantitative image recovery. We illustrate the advantages of our framework by applying it to two nonlinear imaging modalities-phase retrieval and optical diffraction tomography.

Artifacts in optical projection tomography due to refractive index mismatch: model and correction

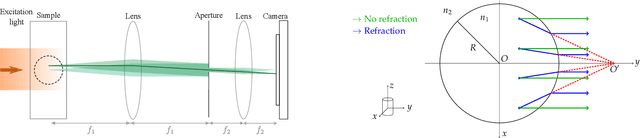
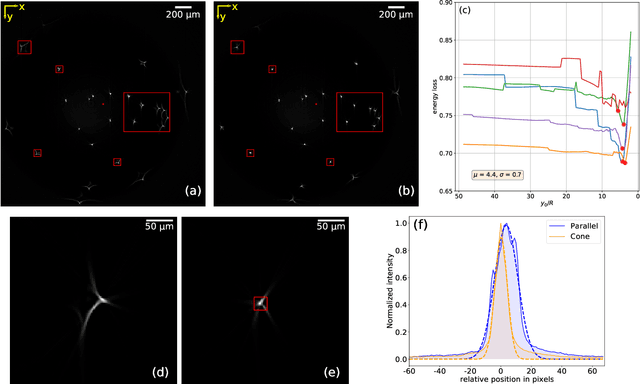
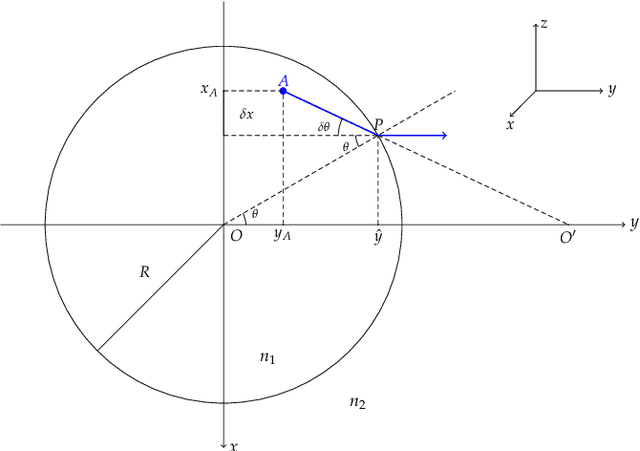
Optical Projection Tomography (OPT) is a powerful tool for 3D imaging of mesoscopic samples, thus of great importance to image whole organs for the study of various disease models in life sciences. OPT is able to achieve resolution at a few tens of microns over a large sample volume of several cubic centimeters. However, the reconstructed OPT images often suffer from artifacts caused by different kinds of physical miscalibration. This work focuses on the refractive index (RI) mismatch between the rotating object and the surrounding medium. We derive a 3D cone beam forward model to approximate the effect of RI mismatch and implement a fast and efficient reconstruction method to correct the induced seagull-shaped artifacts on experimental images of fluorescent beads.

Reservoir Computing meets Recurrent Kernels and Structured Transforms

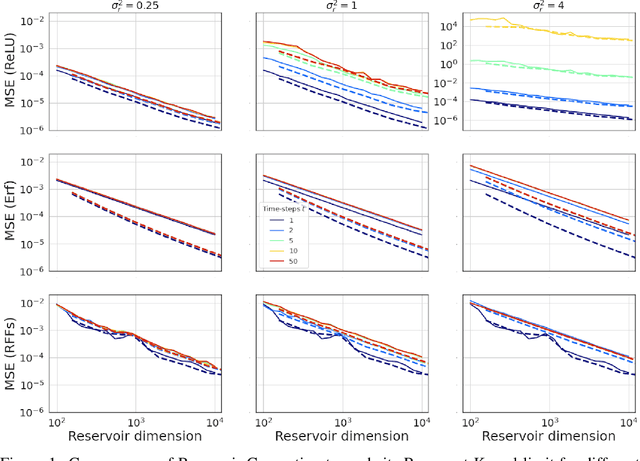
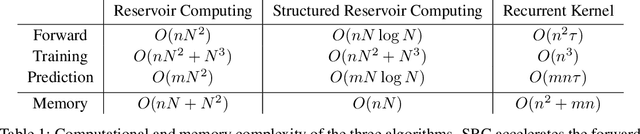
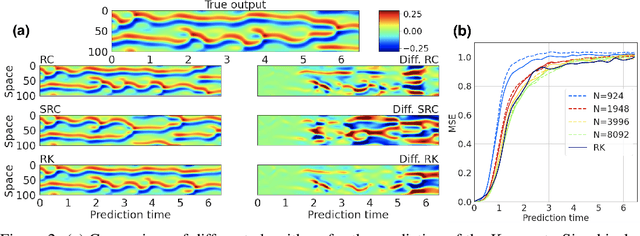
Reservoir Computing is a class of simple yet efficient Recurrent Neural Networks where internal weights are fixed at random and only a linear output layer is trained. In the large size limit, such random neural networks have a deep connection with kernel methods. Our contributions are threefold: a) We rigorously establish the recurrent kernel limit of Reservoir Computing and prove its convergence. b) We test our models on chaotic time series prediction, a classic but challenging benchmark in Reservoir Computing, and show how the Recurrent Kernel is competitive and computationally efficient when the number of data points remains moderate. c) When the number of samples is too large, we leverage the success of structured Random Features for kernel approximation by introducing Structured Reservoir Computing. The two proposed methods, Recurrent Kernel and Structured Reservoir Computing, turn out to be much faster and more memory-efficient than conventional Reservoir Computing.

Kernel computations from large-scale random features obtained by Optical Processing Units

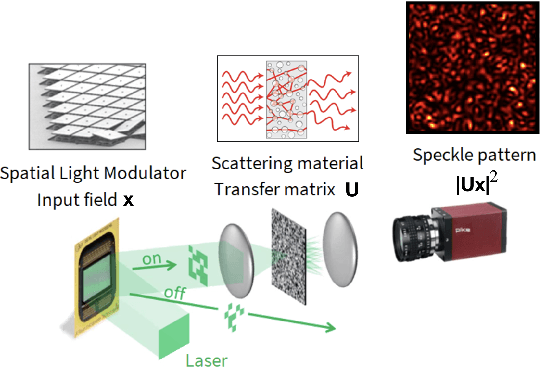
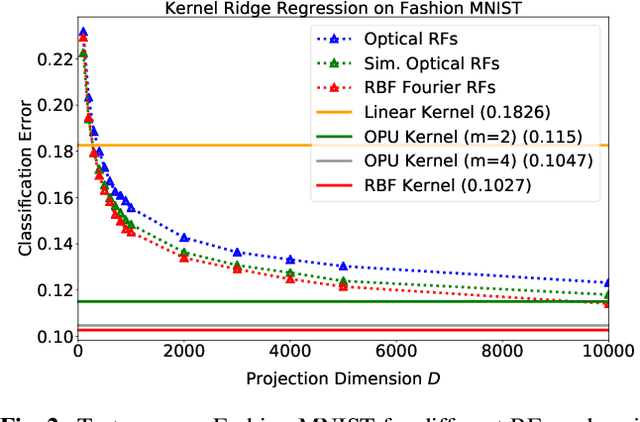
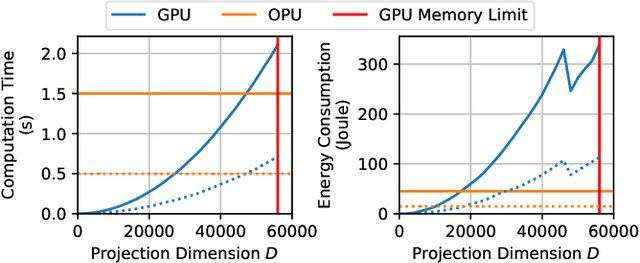
Approximating kernel functions with random features (RFs)has been a successful application of random projections for nonparametric estimation. However, performing random projections presents computational challenges for large-scale problems. Recently, a new optical hardware called Optical Processing Unit (OPU) has been developed for fast and energy-efficient computation of large-scale RFs in the analog domain. More specifically, the OPU performs the multiplication of input vectors by a large random matrix with complex-valued i.i.d. Gaussian entries, followed by the application of an element-wise squared absolute value operation - this last nonlinearity being intrinsic to the sensing process. In this paper, we show that this operation results in a dot-product kernel that has connections to the polynomial kernel, and we extend this computation to arbitrary powers of the feature map. Experiments demonstrate that the OPU kernel and its RF approximation achieve competitive performance in applications using kernel ridge regression and transfer learning for image classification. Crucially, thanks to the use of the OPU, these results are obtained with time and energy savings.

Scaling up Echo-State Networks with multiple light scattering

Echo-State Networks and Reservoir Computing have been studied for more than a decade. They provide a simpler yet powerful alternative to Recurrent Neural Networks, every internal weight is fixed and only the last linear layer is trained. They involve many multiplications by dense random matrices. Very large networks are difficult to obtain, as the complexity scales quadratically both in time and memory. Here, we present a novel optical implementation of Echo-State Networks using light-scattering media and a Digital Micromirror Device. As a proof of concept, binary networks have been successfully trained to predict the chaotic Mackey-Glass time series. This new method is fast, power efficient and easily scalable to very large networks.

Experimental robustness of Fourier Ptychography phase retrieval algorithms

Fourier ptychography is a new computational microscopy technique that provides gigapixel-scale intensity and phase images with both wide field-of-view and high resolution. By capturing a stack of low-resolution images under different illumination angles, a nonlinear inverse algorithm can be used to computationally reconstruct the high-resolution complex field. Here, we compare and classify multiple proposed inverse algorithms in terms of experimental robustness. We find that the main sources of error are noise, aberrations and mis-calibration (i.e. model mis-match). Using simulations and experiments, we demonstrate that the choice of cost function plays a critical role, with amplitude-based cost functions performing better than intensity-based ones. The reason for this is that Fourier ptychography datasets consist of images from both brightfield and darkfield illumination, representing a large range of measured intensities. Both noise (e.g. Poisson noise) and model mis-match errors are shown to scale with intensity. Hence, algorithms that use an appropriate cost function will be more tolerant to both noise and model mis-match. Given these insights, we propose a global Newton's method algorithm which is robust and computationally efficient. Finally, we discuss the impact of procedures for algorithmic correction of aberrations and mis-calibration.